УДК 519.6
Алибиев Д.Б.,
Кажикенова А.Ш.
ТЕОРЕМА О СХОДИМОСТИ
линейной
задачи океанологии
Многие гидродинамические модели для решения определения качества воды океана и разных водоемов сводятся к решению гидростатических моделей атмосферы и океана. Особенность моделей заключается в том, что системы уравнений интегро-дифференциальные.
Пусть дана система уравнений линейной стационарной модели океана
![]() (1)
(1)
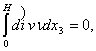
![]() (2)
(2)
![]() S – граница области
S – граница области ![]() (3)
(3)
В области ![]() аппроксимируем уравнения
(1), (2)
аппроксимируем уравнения
(1), (2)
![]() (4)
(4)
![]() (5)
(5)
![]() Sh - граница области
Sh - граница области ![]() . (6)
. (6)
Рассмотрим
итерационный метод для численного решения задачи (4) - (6):
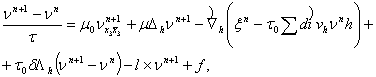 (7)
(7)
![]() (8)
(8)
где вектор
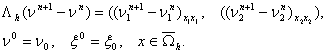
Разностная схема (4) – (6) имеет единственное решение. Для решения этой
схемы справедлива оценка
![]()
Данная схема имеет первый порядок аппроксимации и сходится со
скоростью ![]() . Оценим скорость сходимости итерационного метода к решению
задачи (4), (6). Введем следующие обозначения
. Оценим скорость сходимости итерационного метода к решению
задачи (4), (6). Введем следующие обозначения
![]()
где ![]() решения задачи (4) - (6).
Тогда для
решения задачи (4) - (6).
Тогда для ![]() получим однородные уравнения
получим однородные уравнения
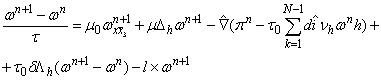 (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
Из формулы (10) найдем ![]() , подставим найденное значение в (9), в результате получим
, подставим найденное значение в (9), в результате получим
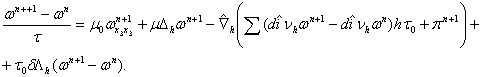 (12)
(12)
Умножим выражения (10), (12) на ![]() просуммируем по
точкам области
просуммируем по
точкам области ![]() соответственно, в
результате этого будем иметь
соответственно, в
результате этого будем иметь
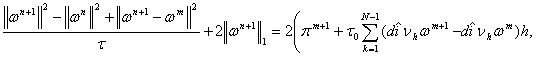
![]() (13)
(13)
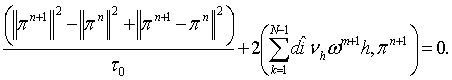 (14)
(14)
Преобразуем слагаемые
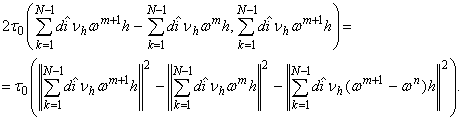 (15)
(15)
Учитывая (15), умножим (13), (14) на ![]() и сложим их, в
результате получим
и сложим их, в
результате получим
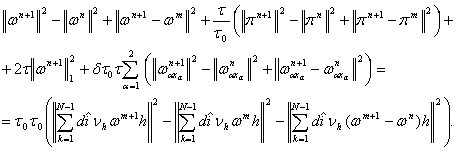 (16)
(16)
Заметим, что существует положительная
постоянная ![]() , не зависящая от шага сетки. Для него справедливо
неравенство
, не зависящая от шага сетки. Для него справедливо
неравенство
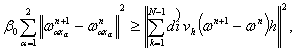 (17)
(17)
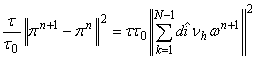 . (18)
. (18)
Отбросим отрицательные слагаемые в правой части (16) и
![]() возьмем так, чтобы (
возьмем так, чтобы (![]() -
-![]() )>0. Тогда с учетом (17), (18) имеем
)>0. Тогда с учетом (17), (18) имеем
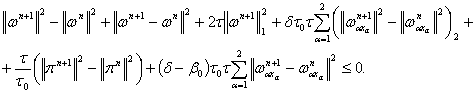 (19)
(19)
Отсюда видно, что ![]() при
при ![]() Но из формулы (19)
получить скорость сходимости затруднительно. Для получения оценки скорости
сходимости сделаем следующие преобразования: умножим (19) на любую сеточную
функцию, которая обращается в ноль на границе, затем просуммируем по точкам
области. В результате имеем:
Но из формулы (19)
получить скорость сходимости затруднительно. Для получения оценки скорости
сходимости сделаем следующие преобразования: умножим (19) на любую сеточную
функцию, которая обращается в ноль на границе, затем просуммируем по точкам
области. В результате имеем:
![]()
![]()
Отсюда получаем следующую оценку
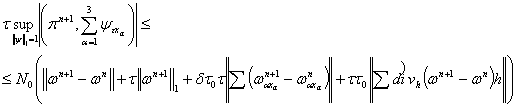 (20)
(20)
или
![]() (21)
(21)
С учетом формулы (17) из формулы (20) получим
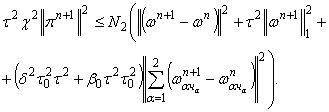 (22)
(22)
Умножим неравенство (22) на положительное число ![]() сложим его с формулой
(19). Полагая, что
сложим его с формулой
(19). Полагая, что ![]() получим
получим
![]()
![]() (23)
(23)
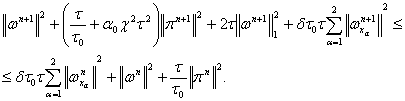
Применяя неравенства
![]()
![]()
из формулы (23) получим
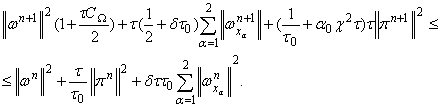
Последнее неравенство перепишем в виде
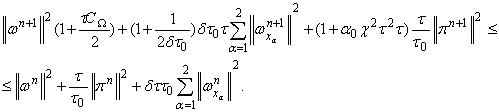 Отсюда
получаем
Отсюда
получаем
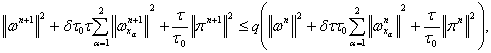
где
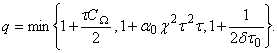
Нами доказан следующая теорема
Теорема 1. Пусть выполнены условия (23). Тогда решение задачи (7)
– (8) сходится к решению задачи (4) –
(6) со скоростью геометрической прогрессии.