Математика/5. Математическое моделирование

К.ф.-м.н. Буздов А.К.

Кабардино-Балкарский государственный аграрный университет, Россия

Определение параметров в двумерных задачах

криодеструкции биоткани.

Криохирургическая операция состоит в уничтожении клеток в локальном, четко ограниченном объеме биоткани, занимаемом злокачественной опухолью. Гибель клеток достигается в результате разрыва мембран образующимися при криогенном охлаждении кристаллами льда внеклеточной и внутриклеточной воды, а также осмотического разбухания при оттаивании биоткани. В связи с этим весьма актуальным является математическое моделирование тепловых процессов в замораживаемой биоткани, требующее разработки эффективных методов решения задач типа Стефана, особенностью которых в криобиологии является пространственная локализация и существование предельных стационарных решений.

Биоткань может охлаждаться криохирургическими инструментами различной формы (плоской, цилиндрической и т.д.). В том случае, когда инструмент плоский и достаточно длинный, можно пренебречь краевыми эффектами, возникающими вблизи концов. Тогда процесс распространения тепла в биоткани будет моделироваться двумерной начально-краевой задачей типа Стефана.

Постановка и решение указанной выше прямой задачи для прямоугольной области рассмотрена в [1]. Соответствующие уравнения и дополнительные условия выглядят следующим образом:

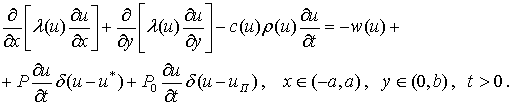(1)

,

,

,

,

,

,

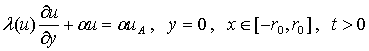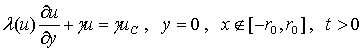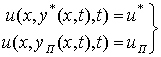(2)

Здесь l(u), c(u), r(u) - коэффициенты теплопроводности, теплоемкости и плотности биоткани соответственно; 2r₀ - ширина плоского криоинструмента; u_A=u_A(t) - температура его охлаждающей поверхности u_C - температура окружающей среды; a - коэффициент теплообмена на участке [-r₀,r₀]; g - коэффициент теплообмена с окружающей средой; - температура биоткани, до которой еще не дошел холод; u^* - температура замораживания биоткани, u_П - температура криопоражения.

Определению подлежит функция температуры u=u(x,y,t), а также пара изотермических поверхностей y^*(x,t), y_П(x,t), на которых температура биоткани равна, соответственно, u^*, u_П. a, b - постоянные, характеризующиеся тем, что вне рассматриваемого прямоугольника температура постоянна и равна .

Предполагается, что коэффициенты C(u), r(u), l(u) могут иметь разрывы типа скачка при u=u^* и u=u_П и что

. (3)

Для определения приближенных значений температуры u(x,y,t) и положения изотермических поверхностей, отвечающих значениям u(x,y,t)=u^*, u(x,y,t)=u_П предлагается следующий алгоритм.

Вводится функция:

,

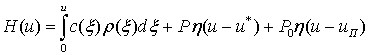которая при u=u^* и u=u_П имеет скачки P и P₀ соответственно; h(x) - функция Хевисайда.

Уравнение (1) теперь можно переписать в виде

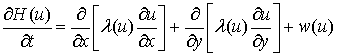. (4)

Производится сглаживание H(u), l(u) по u на интервалах

, где

и при k®¥. В результате сглаживания получаются последовательности ограниченных гладких функций H^k(u), l^k(u), сходящихся при k®+¥ и u¹u^* и u¹u_П, соответственно к H(u), l(u), причем

. (5)

Задача Стефана (1), (2) заменяется аппроксимирующей «сглаженной» задачей:

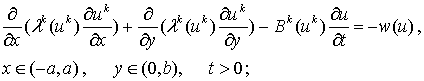(6)

,

,

,

,

,

.

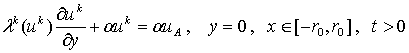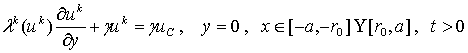Следует отметить что условия (2) на изотермических поверхностях здесь содержатся в уравнении (6). Предполагая, что решение задачи (6) существует и является достаточно гладким, к этой задаче применяется локально-одномерный метод. Приведем схему локально-одномерного метода, когда задача (6) решается в прямоугольной области. Введем произвольную неравномерную сетку:

и обозначим - значение искомой функции в точке (x_i,y_i) в момент времени t_n=nt. Пусть - значение искомой функции на полуслое. Будем считать, что отрезок [-r₀,r₀] разбит на m узлов. Локально-одномерная схема для задачи (6) будет иметь следующий вид:

,

,

;

;

,

.

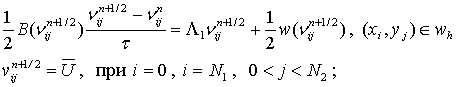
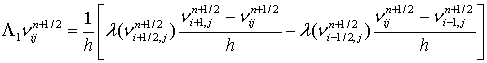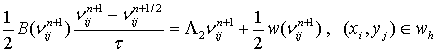
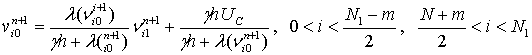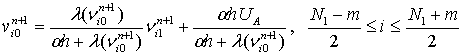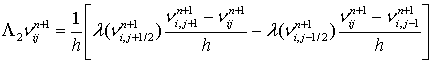Здесь ,

.

Из написанных выше уравнений видно, что для нахождения значения n (при t=t_j+1) на (j+1)-м временном слое по известному значению на j-м временном слое нужно последовательно решать две серии одномерных задач, соответственно, по координатам x и y. Каждая такая задача представляет собой нелинейную алгебраическую систему с трехдиагональной матрицей, и для ее решения лучше пользоваться методом прогонки совместно с каким-либо итерационным методом. В настоящей работе использовался итерационный метод Ньютона. При определении nⁿ⁺¹ методом итераций коэффициенты c, r, l можно брать на предыдущей итерации [2,3]. Подробнее с методом Ньютона можно ознакомиться в [4]. Алгоритм для приближенного решения одномерной задачи Стефана разностным методом со сглаживанием коэффициентов получается отсюда как частный случай.

Вернемся теперь к задаче (6) и рассмотрим несколько более подробно граничные условия:

,

.

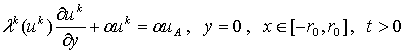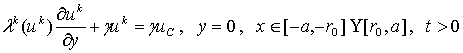Здесь коэффициенты a, g являются коэффициентами теплообмена с поверхностью криоинструмента и окружающей средой соответственно. Для коэффициента a диапазон его изменения более или менее установлен, чего нельзя сказать о коэффициенте g. В связи с этим имеет право на существование следующий метод определения коэффициента g и тем самым соответствующего ему граничного условия. Для определенности рассмотрим участок границы xÎ[r₀,a] (участок xÎ[-a,-r₀] рассматривается аналогично).

Неизвестное граничное условие будет решением следующей последовательности одномерных начально-краевых задач:

,

,

,

.

Здесь значению tⁿ отвечает момент времени nt, где t - шаг по времени в двумерной краевой задаче. Из сказанного выше следует, что одномерные задачи на отрезках [-a,-r₀], [r₀,a] необходимо решать на каждом шаге по времени в исходной двумерной задаче. Таким образом, неизвестное граничное условие 3-го рода заменяется условием 1-го рода.

Алгоритм решения описанной выше одномерной задачи известен. Следует отметить, что недостатком указанного способа определения граничного условия является то, что мы пренебрегаем теплообменом между биотканью и внешней средой, а также влиянием на границу уже охлажденной части биоткани.

В постановке обратной задачи по определению, наряду с искомыми в прямой задаче функциями, какого-либо постоянного параметра в уравнении или краевых условиях дополнительно присутствует условие:

u(x_Д,y_Д,t_Д)=u_Д , x_ДÎ(0,2a), y_ДÎ(0,b), t_Д>0. (Д)

В предлагаемом методе решения необходимо, чтобы определяемый параметр зависел от значения u_Д монотонно. Подобная зависимость коэффициентов теплообмена a и g, а также параметра нелинейности b из (1) вытекает из физического смысла задачи, что подтверждается и при расчетах. При выполнении этих условий решение обратной задачи осуществляется с использованием метода решения соответствующей прямой задачи. А именно, при различных значениях искомого параметра решается прямая задача до тех пор, пока значение вычисленной функции с достаточной точностью не совпадет со значением из дополнительно заданного условия. Порядок изменения параметра можно осуществлять различными способами. Например, методом половинного деления.

Литература:

1. Буздов Б.К. Численно-аналитические методы решения двумерных задач типа Стефана в криомедицине. – Дис. канд. физ.-мат. наук. – Киев, 1995.

2. Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана. ЖВМ и МФ, 1965, т.5, №5, с. 816-827.

3. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. - М.: Наука, 1978. - 589с.

4. Соболев С.Л. Лекции по уравнениям математической физики. - М.: Наука, 1966. - 433с.