Д.т.н. Сальников А.Н., к.т.н. Котина Н.М., асс. Вавилина Н.А.

Саратовский государственный технический

университет имени Гагарина Ю.А., 410054 г. Саратов, Россия

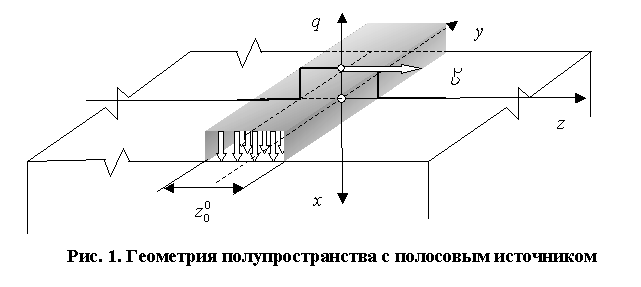
Кинетика нагрева полупространства полосовым подвижным источником постоянной мощности

Предположим, что ширина контакта в направлении вектора скорости имеет величину . Тогда в качестве тепловой модели контакта можно выбрать следующую: по полупространству в положительном направлении оси oz со скоростью движется бесконечно протяженный по у поверхностный полосовой источник постоянной мощности q (рис. 1).

Уравнение, описывающее процесс установления температуры в теле, относится к классу параболических уравнений:

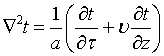. (1)

При решении уравнения (1) зададимся следующими краевыми условиями: границу полупространства всюду, исключая зону действия источника, считаем адиабатической. На контакте действует тепловой источник q(0,0):

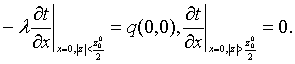(2)

Учтем обычное условие убывания температура на бесконечности. Тогда получим еще два краевых условия:

(3)

Функция источника удовлетворяющая условию (2), для теплопроводящего тела – полупространства запишется следующим образом:

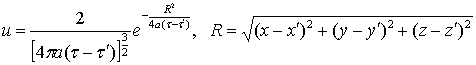. (4)

Если принять, что источник движется по закону z'—υt, перейти в подвижную систему координат, связанную с источником, учесть, что общее тепловыделение источника тепла Q, причем dQ = qdy'gz'dτ, то элементарное повышение температуры в любой точке x > 0 определяется функцией

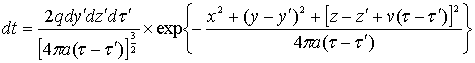. (5)

Для получения решения задачи (1) – (3) на основании общих теорем математической физики проинтегрируем функцию источника (5) по площадке источника и времени:

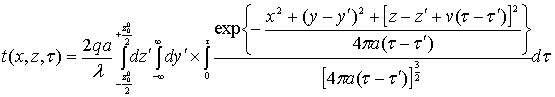. (6)

При τ→∞ функция (6) описывает установившийся тепловой режим :

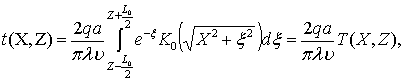(7)

где Х = , Z = , L₀ = , K₀ - модифицированная функция Бесселя второго рода нулевого порядка.

Определим скорость теплового процесса как производную от температуры по времени:

(8)

где Т'_z определяется дифференцированием (7):

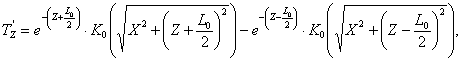(9)

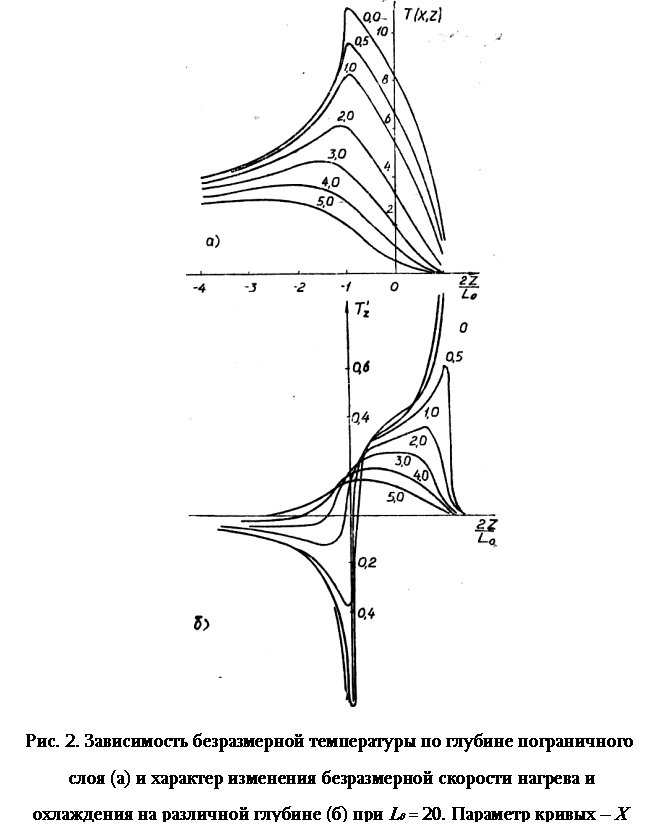
На рис. 2 представлены функции Т и в зависимости от глубины поверхностного слоя и координаты поверхности. Анализ показывает, что при приближении передней кромки источника к заданной точке полупространства по всей глубине поверхностного слоя происходит нагрев, причем область с максимальной скоростью нагрева смещается к задней кромке источника для более глубоких слоев. После прохождения источника скорость нагрева стремится к нулю, а затем меняет знак – происходит охлаждение. При этом более удаленные от поверхности участки пограничного слоя продолжают нагреваться со скоростью, всегда большей скорости охлаждения, независимо от глубины. Увеличение площади контакта приводит к увеличению времени действия теплового источника и, как следствие этого, – к уменьшению скорости теплового процесса на любой глубине.

Наглядные картины распределения поля температур и скоростей тепловых процессов дают изотермы и линии постоянной скорости теплового процесса, позволяющие выделять в поверхностном слое зоны нагревания до заданной температуры с фиксированной скоростью (рис. 3).

Для того, чтобы объединить указанные параметры, то есть рассмотреть тепловую задачу поверхностного слоя как задачу кинетики, введем функцию температуры поверхностного слоя, скорости теплового процесса и различных условий на контакте {С₁}, которая обращается в нуль при изменении указанных переменных:

Ф(Т, ,{С,}) = 0 . (10)

Самый общий способ построения функции (10) заключается в следующем. Предположим, что равенство (7) разрешено относительно Z/L₀, то есть Z/L₀ = =f(Х,Т(Х)). Подставим это решение в (9):

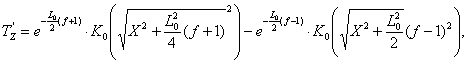(11)

что дает связь скорости теплового процесса и температуры с условиями контактирования.

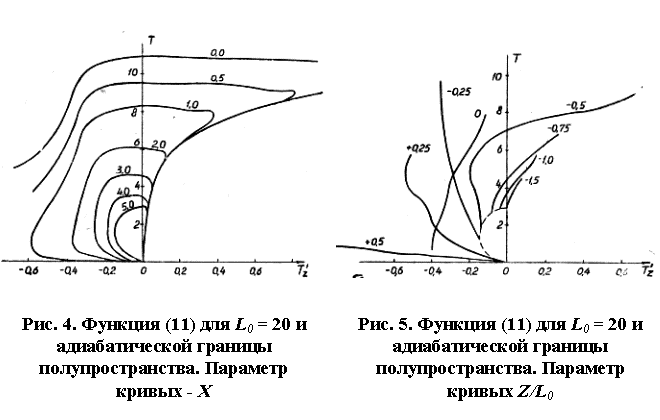
Типичные зависимости (11) для случая отсутствия теплообмена с границы поверхностного слоя представлены на рис. 4. Для того, чтобы наглядно проследить развитие теплового процесса в поверхностном слое, можно построить зависимость для каждой точки полупространства (рис. 5).

Можно и дальше конкретизировать приведенные закономерности и получать большое количество полезной информации. Здесь же ограничимся приведенными сведениями, поскольку указанная конкретизация может быть легко осуществлена для любой схемы нагрева путем вычислений функции (7), (8) и (9).

Литература

1. Сипайлов В.А. Тепловые процессы при шлифовании и управление качеством поверхности. – М.: Машиностроение. 1978.–167 стр.