УДК 519.2:669.5

д.т.н., проф. Рутковский А.Л., к.т.н. Болотаева И.И., к.т.н. Ковалева М.А.

ФГБОУ ВПО «Северо-Кавказский горно-металлургический институт (государственный технологический университет)», кафедра «Теории и автоматизации металлургических процессов и печей»

ПРИМЕНЕНИЕ МЕТОДОВ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА ПРИ ОБРАБОТКЕ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ ПРИМЕНИТЕЛЬНО К ЦИНКОВОМУ ПРОИЗВОДСТВУ

Задача рационального планирования эксперимента при этом сводится к построению некоторого плана эксперимента – набора опытов, обладающего определенными, наперед заданными свойствами. К их числу могут быть отнесены: условие ортогональности входных переменных x_i, композиционности плана, ротатабельности, минимума числа опытов и др. [1,2].

Покажем, что планы, обладающие перечисленными выше свойствами, могут быть получены и в пассивном эксперименте при анализе статистического материала. Напомним основные трудности, связанные с построением моделей методами математической статистически-корреляционного и регрессивного анализа.

Значительная трудность здесь состоит в определении рационального объема выборки. С одной стороны выборка не должна быть чрезмерно большой, так как ее формирование, подготовка к счету и собственно счет требует значительных затрат времени. С другой стороны объем выборки снизу ограничен требованиями статистической достоверности определенных параметров модели. В частности, для модели вида

, (1)

статистическая достоверность параметров , коэффициентов корреляции может быть оценена по величинам доверительных интервалов [3-7, 9].

(2)

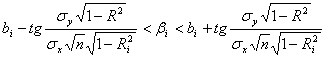(3)

где r_i,j, ρ_i,j - эмпирический и истинный коэффициенты корреляции i, j=1,2,…, i≠j; tg – параметр нормированной функции Лапласса [8]; n – число элементов в выборке; R – коэффициент множественной корреляции y со всеми параметрами x_i; R_i - коэффициент множественной корреляции данного параметра x_i с другими параметрами x_j, i≠j без параметра y ; σ_i, σ_y - средние квадратические отклонения параметров x_i, y.

Очевидно, что указанные выше параметры при сборе статистического материала неизвестны и поэтому либо исследования проводят в несколько этапов, изменяя n по величинам доверительных интервалов, либо сразу заведомо завышают объем выборки.

Задача формирования выборки осложнена еще тем, что параметры должны быть хорошо (в пределах ) проварьированы и распределены по закону, близкому к нормальному.

Следует помнить так же о том, что матрица систем нормальных уравнений, формируемые из статистического материала при построении модели, как правила, бывают плохо обусловлены, особенно для параболических моделей и моделей, содержащих парные эффекты и эффекты более высоких порядков, явление плохой обусловленности в свою очередь резко сужает допустимую ширину доверительных интервалов.

Существенную трудность при моделировании представляет и то, что моделирование ведется в два этапа: на первом - ставится задача моделирования, определяется вид модели, формируется массив исходной информации; на втором – математиками осуществляется непосредственно построение модели.

Применение методов теории планирования эксперимента при организации массивов исходной информации в значительной степени снижают расстояние между объектами моделирования и моделирующей организации, что не дает непосредственно на объекте оценить параметры модели.

Будем считать, что гистограммы параметров, входящих в модель, нами уже построены. В таком случае значениям параметров, близким по величине к моде, присвоим кодированное значение ноль, а значениям отстоящим от «нулевого» на интервал ±Δi соответственно «+i» и «-i». Для простоты дальнейших вычислений следует стремиться к тому, чтобы координаты точек «-i», «ноль», «+i», величины интервалов Δi были, по возможности, целые, четные числа.

Величину интервала следует выбирать так, чтобы в точках «+i», «-i» имелось достаточно статистического материала для дублированной реализации планированного эксперимента. Кроме того, для каждого параметра x_i следует определить допустимую погрешность фиксации уровня опыта σ_i.

Исследование следует начать с «центра плана» - набора точек с нулевыми координатами для x_i. Количество параметров, вводимых в модель, следует увеличивать постепенно, наблюдая за величиной дисперсии воспроизводимости в центре плана:

, (4)

где – наблюдаемые значения выходного показателя при значениях входных показателей, зафиксированных на средних уровнях; - среднее значение для центра плана; N - число точек в центре плана.

В том случае, если величина не превышает некоторого допустимого уровня и возможность технологической интерпретации параметров модели не вызывает сомнения, число параметров, введенных в модель, можно ограничить.

Существенной помехой, затрудняющей реализацию плана эксперимента может явиться коррелированность входных параметров x_i. Насколько такая корреляция может быть существенна, можно продемонстрировать на примере моделирования прочности окатышей, рисунок 1.

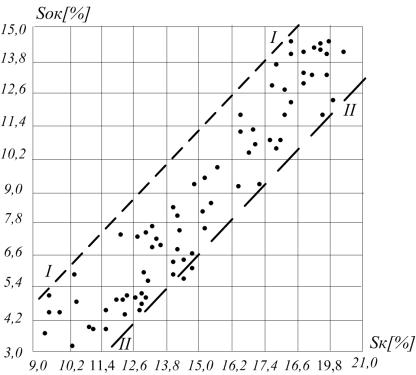
Рисунок 1 - Моделирование прочности окатышей n = f (S_k, S_ok). Явление коррелированности S_k и S_ok (R_Sk,Sok = 0,75). Линии I-I, II-II ограничивают область практической реализуемости эксперимента.

Явление коррелированности можно устранить введением ортогональных переменных U_i = f(x₁,x₂) вида

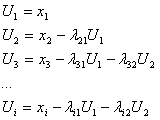(5)

Ортогонализирующие коэффициенты могут быть определены из соотношений

(6)

Отметим, что в предварительном анализе достаточно лишь приближенно оценить λ_i,j, чтобы получить слабо коррелированные переменные U_i, для которых удается сформировать реализуемый план эксперимента. Для примера, согласно рисунку 1, можно найти некоррелированные переменные U₁ = S_k , U₂ = S_ok – 0,651S_k.

Упрощенно считая λ₂₁ = 0,7, получим некорреляционное поле для слабо коррелированных U₁, U₂, рисунок 2 - эквивалентное рисунку 1. На этом поле выделим один из возможных планов эксперимента «опыта» 1, 2, 3, 4, 5, точность фиксации уровней δ_U1 = ±0,7%, δ_U2 = ±0,4%.

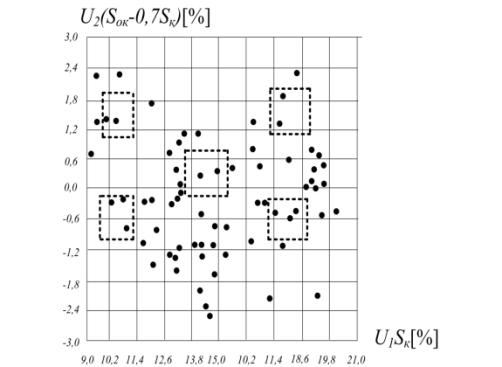
Рисунок 2 - Корреляционное поле слабо коррелированных переменных U₁, U₂.

Согласно выделенному плану эксперимента составим матрицу эксперимента, представленную в виде таблицы. Здесь y - процент разрушившихся в процессе испытаний окатышей.

Таблица

Матрица планированного эксперимента

№ опыта	U1	U2		Количество реализуемости
1	-1	+1	7,8; 10,4	2	9,1
2	-1	-1	10,2; 15,5; 9,2	3	11,7
3	+1	+1	26,6; 28,8; 26,9	3	27,43
4	+1	-1	23,9; 24,2; 22,2	3	23,4
5	0	0	10,6; 9,9	2	10,25

Исходя из таблицы по известным формулам [3,5]

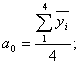
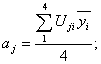
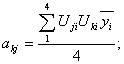k,j = 1,2 (7)

Можно получить модель для кодированных значений переменных U=1, U_2.

(8)

анализ которой указывает на необходимость построения существенно нелинейной модели (значение свободного члена модели 18,05 значительно отличается от среднего значения в центре плана – 10,25). Можно также отметить слабое влияние U₂ на прочность окатышей (величина коэффициента при U₂ соизмерима с точностью фиксации уровня). Наличие «выброса» в «опыте» 2 указывает на существование параметров, не вошедших в план, влияние которых соизмеримо с влиянием анализируемых параметров. Дальнейший анализ позволил определить этот параметр – содержание класса – 44 мкм (α - 44) в концентрате. Для облегчения технологической интерпретации в модель была введена производительность обжиговой машины Q_k. План близкий к дробной реплике ротатабельного плана второго порядка для ортогональных переменных [1], содержащих 31 точку, позволил получить модель (естественные переменные)

(9)

R = 0,91 σ_ост =1,5%.

Отметим, что при планировании экспериментов для ортогонализтрованных переменных U_i планы 2ⁿ позволяют получать квадратичные модели для естественных переменных, так для уравнения (8) будем иметь

(10)

Как видно из (10) коэффициент при x₁² получается совместно с коэффициентом при парном эффекте, но это в предварительном анализе не мешает оценить степень нелинейности модели, выявить потенциальное наличие оптимума.

Таким образом, применение методов планирования эксперимента при обработке статистической информации позволяет значительно улучшить качество исходных данных для моделирования, существенно снизить их объем, n непосредственно на объекте оценить вид и качество модели, которые можно получить из данного статистического материала.

Литература

1. Налимов В.В., Черкова И.А. Статистические методы планирования экстремальных экспериментов. М., Наука, 1965, С. 340.

2. Вознесенский В.А. Статистические методы планирования эксперимента в технико-экономических исследованиях. М.: Статистика, 1975, С. 232.

3. Химельблау Д. Анализ процессов статистическими методами, М., «Мир», 1973, С. 960.

4. Бородюк В.П., Лецкий Э.К. Статистическое описание промышленных объектов. М., «Энергия», 1971, 112 c.

5. Демиденко Е.З. Линейная и нелинейная регрессия. М., Статистика, 1981, С. 302.

6. Круг Г.К., Ласенков А.Н. Планирование эксперимента в условиях временного дрейфа. М., Труды МЭИ, 1966, вып. 67. С. 98.

7. Налимов В.В. Статистические методы описания химических и металлургических процессов. М., Металлургия, 1965, С. 232.

8. Иванова В.М., Калинина В.Н. и др. Математическая статистика. М.: Высшая школа. 1975, С. 452.

9. Рутковский А.Л., Болотаева И.И., Юрошева Т.А. Алгоритм модифицированного симплексного поиска в задаче оптимального управления параметрами процесса электролиза цинка. Научно-технические ведомости СПбГПУ. Информатика. Телекоммуникации. Управление, №4, г. Санкт-Петербург, 2010г, С 142-145.