Докукова Н.А.,
Кафтайкина Е.Н., Конон Н.П.
Белорусский
государственный университет
АНАЛИЗ ОБЩИХ ЗАВИСИМОСТЕЙ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК МНОГОЭЛЕМЕНТНОЙ
ДИНАМИЧЕСКОЙ СИСТЕМЫ С ВНЕШНИМ ИЛИ ВНУТРЕННИМ ЗАТУХАНИЕМ
Введение. Возможность воспроизведения амплитудно-частотных
характеристик звеньев многоэлементной динамической системы по известным
экспериментальным графикам позволяет расшифровать взаимовлияние осциллирующих связей
на общий динамический процесс, принять меры по изменению конструкции для сглаживания
околорезонансных частотных зон во время эксплуатации машины.
Постановка
задачи. Для исследования АЧХ
многоэлементных динамических систем с произвольным числом степеней свободы
используем развитую авторами методику [1-2]. Колебания механической системы с N-степенями свободы на рисунке 1
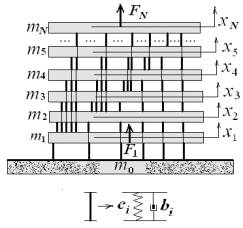
Рисунок 1 -
Общая динамическая схема механической системы с N-степенями
свободы
представима в
матричном - каноническом виде N - линейных дифференциальных уравнений второго порядка [1-2]:
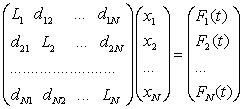 . (1)
. (1)
Здесь введены
обозначения ![]() −
дифференциальные операторы по параметру времени t ; cij – коэффициенты
упругих элементов cj, отнесенных к соответствующим массам mi
−
дифференциальные операторы по параметру времени t ; cij – коэффициенты
упругих элементов cj, отнесенных к соответствующим массам mi ![]() ,
, ![]() ;
; ![]() , bi –
коэффициент вязкого
сопротивления колебаниям тел;
, bi –
коэффициент вязкого
сопротивления колебаниям тел; ![]() – вектор искомых
перемещений масс;
– вектор искомых
перемещений масс; ![]() – вектор внешних
гармонических сил.
– вектор внешних
гармонических сил.
Систему (1) с помощью определенных невырожденных линейных преобразований
можно привести к системе независимых линейных обыкновенных дифференциальных
уравнений порядка 2N, не связных
между собой [3]
![]() , (2)
, (2)
где
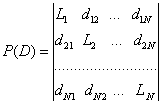 ,
, 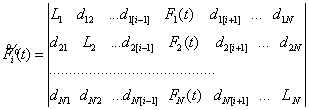 . (3)
. (3)
Поскольку частотные
характеристики описывают реакцию динамического звена на изменение входной
величины по закону гармонических незатухающих колебаний, то в качестве таковой
выберем ![]() , все остальные
, все остальные ![]() . Будем исследовать, например, влияние вибраций двигателя на
АЧХ многомассовой системы. Выходная величина динамических звеньев определятся
по закону синуса, с той же частотой, но с другой амплитудой и фазой.
. Будем исследовать, например, влияние вибраций двигателя на
АЧХ многомассовой системы. Выходная величина динамических звеньев определятся
по закону синуса, с той же частотой, но с другой амплитудой и фазой.
Применим операторный метод к системе уравнений (2) учитывая, что в
начальный момент времени вся исследуемая механическая система находилась в
состоянии покоя: ![]() (0)=0,
(0)=0, ![]() (0)=0. Тогда операторы dij, Li перейдут к новым
(0)=0. Тогда операторы dij, Li перейдут к новым ![]() , P(D)
, P(D)![]() , где
, где ![]() , вектор искомых перемещений будет заменен
, вектор искомых перемещений будет заменен ![]()
![]()
![]() , входная функция
, входная функция ![]() преобразуется к
преобразуется к ![]() . Задача об определении АЧХ всех звеньев сложной механической
системы сведена к задаче об определении модуля вектора решений
. Задача об определении АЧХ всех звеньев сложной механической
системы сведена к задаче об определении модуля вектора решений ![]() системы
алгебраических уравнений
системы
алгебраических уравнений
![]() (4)
(4)
где
![]() , (5)
, (5)
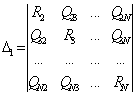 ,
, 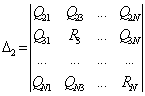 , ,…,
, ,…,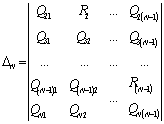 , (6)
, (6)
![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() . (7)
. (7)
Заменим параметр p на iw в равенствах (7). Выделим из них полиномы с
четными и нечетными степенями параметра w.
![]() , (8)
, (8)
![]() (9)
(9)
![]() (10)
(10)
![]() , (11)
, (11)
![]() (12)
(12)
![]() ,
(13)
,
(13)
![]() , (14)
, (14)
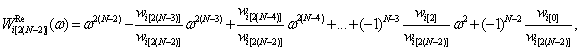 (15)
(15)
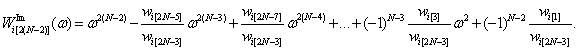 (16)
(16)
Здесь первые
коэффициенты ![]() ,
, ![]() для полинома (8),
для полинома (8), ![]() ,
, ![]() для алгебраического
дополнения
для алгебраического
дополнения ![]() ,
, ![]() ,
, ![]() для D2,…,DN. Положим, что все полиномы
(9), (10), (12), (13), (15) и (16) допускают определение корней в области
действительных и комплексных чисел. Тогда могут появляться сомножители вида:
для D2,…,DN. Положим, что все полиномы
(9), (10), (12), (13), (15) и (16) допускают определение корней в области
действительных и комплексных чисел. Тогда могут появляться сомножители вида:
![]() (w2 + ai2)×…×(w2 - bj2)×…×(w 4 + 2ykw2 + yk2+ оk2) , (17)
(w2 + ai2)×…×(w2 - bj2)×…×(w 4 + 2ykw2 + yk2+ оk2) , (17)
![]() (w2 + cm2)×…×(w2 - gl2)×…×(w 4 + 2зrw2 + зr2 + qr2) , (18)
(w2 + cm2)×…×(w2 - gl2)×…×(w 4 + 2зrw2 + зr2 + qr2) , (18)
![]() (w2 + hi2)×…×(w2 - mj2)×…×(w 4 + 2ukw2 + uk2 + sk2) , (19)
(w2 + hi2)×…×(w2 - mj2)×…×(w 4 + 2ukw2 + uk2 + sk2) , (19)
![]() (w2 + km2)×…×(w2 - fl2)×…×(w 4 + 2hrw2 + hr2 + zr2) , (20)
(w2 + km2)×…×(w2 - fl2)×…×(w 4 + 2hrw2 + hr2 + zr2) , (20)
![]() (w2 + qi2)×…×(w2 - sj2)×…×(w 4 + 2ukw2 + uk2 + tk2) , (21)
(w2 + qi2)×…×(w2 - sj2)×…×(w 4 + 2ukw2 + uk2 + tk2) , (21)
![]() (w2 + rm2)×…×(w2 - yl2)×…×(w 4 + 2erw2 + er2 + vr2) , (22)
(w2 + rm2)×…×(w2 - yl2)×…×(w 4 + 2erw2 + er2 + vr2) , (22)
где все ai, bj, yk, ok, cm, gl, зr, qr, hi, mj, uk, sk, km, fl, hr , zr, qi , sj , uk , tk , rm , yl , er , vr-
- действительные числа, причем ![]() для формулы (17),
для формулы (17), ![]() для формулы (18),
для формулы (18), ![]() для формулы (19),
для формулы (19), ![]() для формулы (20),
для формулы (20), ![]() для формулы (21),
для формулы (21), ![]() для формулы (22).
для формулы (22).
Амплитудно-частотные характеристики
![]()
![]() каждого из входящих в
механическую систему элементов, если Ф
=1 м/с2,
будут вычисляться по формулам
каждого из входящих в
механическую систему элементов, если Ф
=1 м/с2,
будут вычисляться по формулам
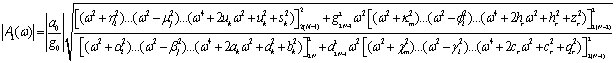 , (23)
, (23)
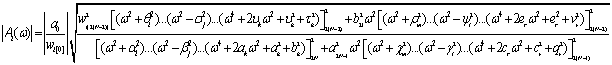 ,
(24)
,
(24)
здесь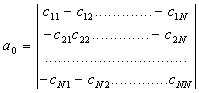 ,
,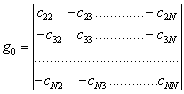 ,
,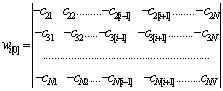 .
.
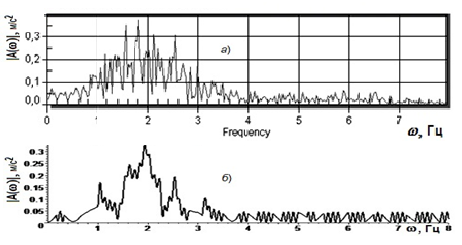
Рисунок 2 – Экспериментальная
амплитудно-частотная характеристики ускорений остова трактора под кабиной с
пружинной подвеской - а и приближенная АЧХ, найденная по
аналитической формуле (23) - б
Представленный расчет является условным, более точное соответствие
графиков на рисунках 2 а и б следует разрабатывать нанесением
координатной сетки на экспериментальную кривую и заполнением таблицы данных,
содержащей значительно большее количество.
Выводы. По известному экспериментальному
графику амплитудно-частотных характеристик многоэлементных динамических систем
разработана методика расшифровки взаимовлияния осциллирующих звеньев на общий
динамический процесс. Установлена закономерность влияния большого числа
линейных осцилляторов и конфигураций их связей на вид амплитудно-частотной
характеристики.
ЛИТЕРАТУРА
1. Dokukova N.A. and
P.N. Konon. General laws governing in mechanical vibratory systems// Journal of
Engineering Physics and Thermophysics, 2006, Volume 79, Number 4, Pages
824-831, Publisher Springer New York, ISSN: 1062-0125.
2. Dokukova N.A., P.N.
Konon and E.N. Kaftaikina. Nonnatural vibrations of hydraulic shock-absorbers//
Journal of Engineering Physics and Thermophysics, 2008, Volume 81, Number 6,
Pages 1191-1196, Publisher Springer New York, ISSN: 1062-0125.
3. Кафтайкина Е.Н., Докукова Н.А.,
Окрут
Д.И. Программа
расчета коэффициентов характеристического уравнения системы уравнений динамики
механических объектов. Реестр
зарегистрированных компьютерных программ в Национальном центре интеллектуальной
собственности Республики Беларусь.- 16.04.2012.