Технические науки/6. Электротехника и радиоэлектроника

Ст. преп. Мирзакулова Ш.А.

Алматинский университет энергетики и связи

ИССЛЕДОВАНИЕ

СЕТЕВОГО ТРАФИКА МЕТОДОМ FNN

M. B. Kennel разработал метод FNN (False Nearest Neighbours, ложного ближайшего соседа), который предназначен для определения минимальной достаточной размерности вложения был предложен [1, 2].

В [3] описано, что корреляционной размерностью можно характеризовать структурированность аттрактора. В [4] отмечается, что корреляционную размерность можно определить по экспериментальным данным, не зная всех переменных динамической системы. На рисунке 1 показана зависимость изменения корреляционной размерности D_c от размерности вмещения (n). Чем выше значение D_c тем сложнее сигнал.

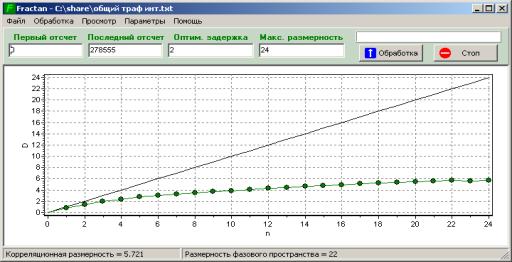
Рисунок 1 – Зависимость изменения корреляционной размерности D_c

от размерности вмещения (n)

В свою очередь корреляционная размерность D_c показывает степень сложности поведения динамической системы и минимальное количество размерностей пространства, в котором размещаются траектории.

В нашем случае корреляционная размерность D_c равна 5,721 и n=22. В этой точке корреляционная размерность явного насыщения не имеет и размерность вмещения n достаточно большое.

В программе TISEAN [5] проверим достаточность минимально необходимой размерности лагового пространства (рисунок 2), на котором видно, что с увеличением величины лагового пространства количество ложных соседей уменьшается и, что число ложных соседей будет равно нулю как раз при значении величины лагового пространства равного 22 или 23.

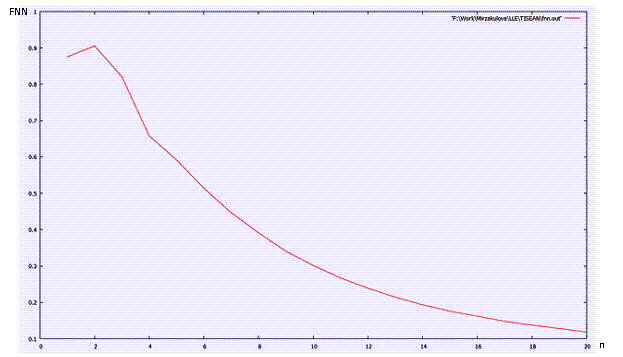
Рисунок 2 – Зависимость количества ложных соседей от размерности лагового пространства

Вывод:

- рассматриваемый процесс D_c от n выраженного насыщения не имеет;

- зависимость количества ложных соседей от размерности лагового пространства подтвердило минимальное значение необходимой размерности лагового пространства равного 22 или 23;

- исследуемый процесс зашумлен и порождающая система является не случайной, а управляемой большим числом параметров.

Литература:

1. http://novainfo.ru/archive/1/prikladnaya-nelineynaya-dinamika

2. M. B. Kennel, R. Brown, and H. D. I. Abarbanel, Determining embedding dimension for phase-space reconstruction using a geometrical construction // Phys. Rev. A 45, 3403 (1992).

3. Смирнов А. А., Даниленко Д. А., Мелешко Е. В. Метод обнаружения вредоносного программного обеспечения. Часть 1. Корреляционный анализ сетевого трафика. IКСЗТ, 2012 №4.

4. Николаева Д. А. Применение метода оценки корреляционной размерности для анализа ЭЭГ человека с заболеванием эпилепсия. – Санкт-Петербург. Дифференциальные уравнения и процессы управления, 2009, том №2, 43-51 с.

5. Меклер А. А. Применение аппарата нелинейного анализа динамических систем для обработки сигналов ЭЭГ. // Вестник новых медицинских технологий – 2007 – Т. ХIV, № 1 – С. 73-77.