Математика/ 4.Прикладная математика.

К.ф.-м.н. Искакова А.С., Касымова А.Н. , Касымова А.Н.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Казахско-турецкий лицей города Астаны

Моделирование интревалов ожидаемых прогнозов социальных выплат страхового портфеля

В связи с этим, маловероятно построение идеального прогноза социальных выплат. Отметим, что значения эмпирической функции выплат представляют собой средний ожидаемое значение или эффективность операции. Тогда риском r_i (i- конечное натуральное число) операции является модуль разности ожидаемого выплата q_i и значения эмпирической функции y_i, то есть r_i =|q_i -y_i|.

По правилу Вальда или по правилу крайнего пессимизма за рекомендуемый прогноз выплат следует принять прогноз со значением

.

Таблица 1

Крайне пессимистические прогнозы доходов страховой компании.

Наименование показателей	Годы
	2006	2007	2008	2009	2010	2011	2012	2013	2014
На случай утраты трудоспособности	-3605,9	-3602,7	-3479,9	-3198,4	-2682,2	-2167,3	-1547,6	-828,1	0,000497
На случай потери кормильца	-3002	-2941,9	-2808,19	-2518,79	-2230,29	-1890,89	-1399,99	-845,693	7,607381
На случай потери работы	-1188	-1185	-1179	-1138	-371,4	-354,5	-288,4	-319,7	7,607

Аналогично по правилу Вальда можно определить крайние оптимистические прогнозы как [9]

.

Так, например, при рассмотрении прогноза выплат страхования имеем r₁= 2,999501, r₂ = 6,199501, r₃ = 128,9995,…, r₉₌ 3608,9 и . Значит, крайне оптимистические прогнозы получаемые значения как

приведены в таблице 2.

Таблица 2

Крайне оптимистические прогнозы выплат страховой компании

Наименование показателей	Годы
	2006	2007	2008	2009	2010	2011	2012	2013	2014
На случай утраты трудоспособности	3612	3615	3738	4019	4536	5050	5670	6390	7318
На случай потери кормильца	3009	3069	3203	3493	3781	4120	4611	5166	6019
На случай потери работы	1188	1190	1196	1237	2004	2021	2087	2056	2383

Таким образом, по результатам данных в таблиц 4 и 5 имеем следующие графики, описывающие эмпирические функции, функции крайних пессимистических и оптимистических прогнозов выплат. [10]

Эмпирическая функция, функции крайних пессимистических и оптимистических прогнозов выплат на случай потери кормильца выглядят следующим образом.

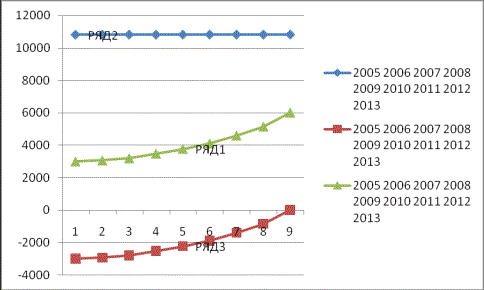
Где ряд 1- функция крайних пессимистических прогнозов, ряд 2- эмпирическая функция, ряд 3 функция крайних оптимистических прогнозов.

Эмпирическая функция, функции крайних пессимистических и оптимистических прогнозов выплат на случай потери работы выглядят следующим образом.

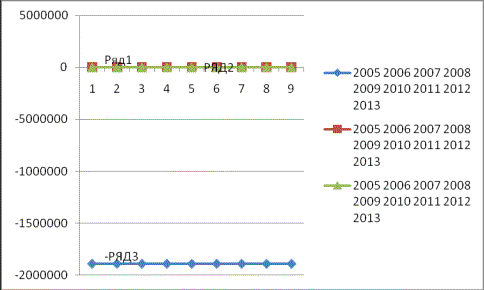
Где ряд 1- функция крайних пессимистических прогнозов, ряд 2- эмпирическая функция, ряд 3 функция крайних оптимистических прогнозов.

Эмпирическая функция, функции крайних пессимистических и оптимистических прогнозов выплат по беременности и родам выглядят следующим образом.

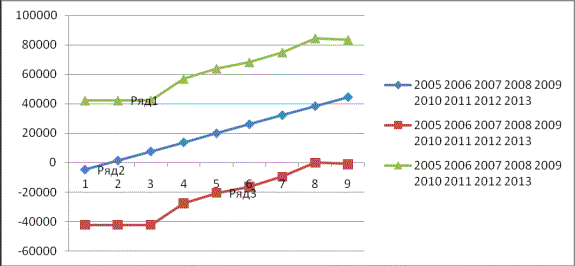
где ряд 1- функция крайних пессимистических прогнозов, ряд 2- эмпирическая функция, ряд 3 функция крайних оптимистических прогнозов.

Эмпирическая функция, функции крайних пессимистических и оптимистических прогнозов выплат пособий по уходу за ребенком до одного года выглядят следующим образом.

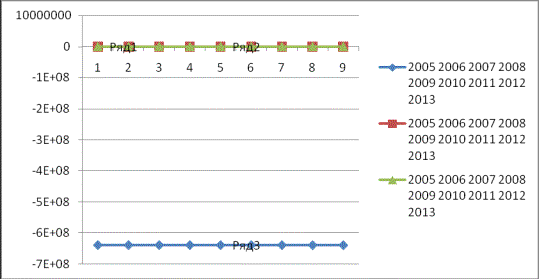
Где ряд 1- функция крайних пессимистических прогнозов, ряд 2- эмпирическая функция, ряд 3 функция крайних оптимистических прогнозов.

Очевидно, что значение прогноза выплат, принимающие значения больше крайних пессимистических и меньше крайних оптимистических прогнозов удовлетворяют следующему условию или

Таким образом, значение прогноза выплат на случай утраты трудоспособности, принимающие значения больше крайних пессимистических и меньше крайних оптимистических прогнозов удовлетворяют следующему условию:

Значение прогноза выплат на случай потери кормильца, принимающие значения больше крайних пессимистических и меньше крайних оптимистических прогнозов удовлетворяют следующему условию:

Значение прогноза выплат на случай потери работы, принимающие значения больше крайних пессимистических и меньше крайних оптимистических прогнозов удовлетворяют следующему условию:

Литература:

1 Демидович Б.П., Марон И.А. Основы вычислительной математики. - Москва: Наука, 1970. - 664 с.

2 Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. – Москва: Наука, 1996. - 265 с.

3 Джонс Дж.К. Методы проектирования. - Москва: МИР, 1986. - 326 c.

4 Карасев А.И., Кремер Н.Ш., Савельева Т.И. Математические методы и модели в планировании. – Москва: Экономика, 1987. 241 с.

5 Калиткин Н.П. Численные методы. - Москва: Наука, 1978. - 221 с.

6 Березин И.С., Жидков Н.П. Методы вычислений часть I,II. - Москва: Наука, 1978. - 63 с.

7 Данилина Н.И., Дубровская Н.С., Кваша О.П., Смирнов Г.Л., Феклисов Г.И. Численные методы. Учебник для техникумов. - Москва: Высшая школа, 1976. - 368 с.

8 Бахвалов Н.С. Численные методы. часть I,II. - Москва: Наука, 1973. - 256 с

9 Боглаев Ю.П. Вычислительная математика и программирование. - Москва: Наука, 1990. - 315 с.

10 Хемминг Р.В. Численные методы. - Москва: Наука, 1972 – 256 с