Математика/ 4.Прикладная математика.
К.ф.-м.н. Искакова А.С.,
Касымова А.Н. , Касымова А.Н.
Евразийский национальный университет им. Л.Н.
Гумилева, Казахстан
Казахско-турецкий лицей города Астаны
Построение
краткосрочных прогнозов социальных выплат страхового портфеля
По
консолидированной финансовой
отчетности АО «Государственный фонд
социального страхования» имеем
статистические данные за последние k лет. Представим эти данные в виде таблицы1.
Таблица 1
|
|
Года |
||
|
|
… |
|
|
|
|
… |
|
|
Нас интересует, как выглядит
функциональная зависимость между xi и yi, где i принимает любые натуральные конечные значения.
Пусть y – функция одной переменной с двумя
параметрами a и b. В качестве набора выбора функций,
из которых будем иметь эмпирическую зависимость, рассмотрим [1]:
1
линейную функцию 
;
2
показательную функцию 
;
3
дробно-рациональную
функцию 
;
4
логарифмическую функцию 
;
5
степенную функцию 
;
6
гиперболическую функцию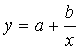 
;
7
дробно-рациональную 
.
Для наилучшего выбора вида
аналитической зависимости y=f(x,a,b)
построим следующие
промежуточные вычисления. На заданном отрезке изменения независимой переменной
выбирают точки, достаточно надежные и, по возможности, далеко отстоящие друг от
друга. Будем считать, что это x1 и xk.Вычислим
среднее арифметическое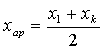 
, среднее геометрическое 
и среднее
гармоническое
.
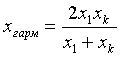По вычисленным значениям независимой переменной находим из статистических данных таблицы 1 соответствующие значения
переменной
, 
, 
для пока еще неизвестной аналитической зависимости y=f(x,a,b). Вычислим среднее арифметическое крайних
значений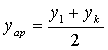 
, среднее геометрическое 
и среднее гармоническое
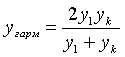. В итоге после
проделанных вычислений оцениванием следующие погрешности [2]:
, 
, 
, 
,
, 
, 
.
Следующая теорема [3] позволяет
определить приближение к функциональной зависимости статистических данных
социальных выплат страховой компании.
Теорема.
Пусть 
. Тогда
1
если e=e1, то в
качестве аналитической зависимости для данного графика хорошим приближением
служит линейная функция 
;
2
если e=e2, то в
качестве аналитической зависимости для данного графика хорошим приближением
служит показательная функция 
;
3
если e=e3, то в
качестве аналитической зависимости для данного графика хорошим приближением
служит дробно-рациональная функция 
;
4
если e=e4, то в
качестве аналитической зависимости для данного графика хорошим приближением
служит логарифмическая функция 
;
5
если e=e5, то в
качестве аналитической зависимости для данного графика хорошим приближением
служит степенная функция 
:
6
если e=e6, то в
качестве аналитической зависимости для данного графика хорошим приближением
служит гиперболическая функция 
7
если e=e7, то в
качестве аналитической зависимости для данного графика хорошим приближением
служит дробно-рациональная функция 
.
Доказательство теоремы можно найти в
разных учебниках по таким направлениям как «Численные методы», «Математический
анализ», «Теория вероятностей и математическая статистика».
Таким образом, из выше предложенной
теоремы определяется вид эмпирической функции f(x,a,b). Коэффициенты a и b эмпирической функции f(x,a,b), можно
определить несколькими способами, оптимальным из которых является метод
наименьших квадратов. Согласно методу наименьших квадратов [4] коэффициенты
a и b должны
удовлетворять следующему равенству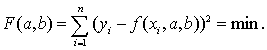 
Найдем частные производные функции F(a,b) по
варьируемым параметрам a и b.
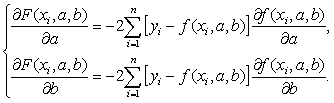
Используя необходимые условия экстремума функции нескольких
переменных при вариации параметров a и b, получим
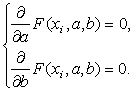
Следовательно, коэффициенты a и b, получаемые по методу
наименьших квадратов, должны удовлетворять следующей системе уравнений [5]
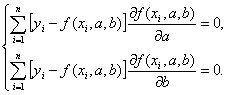(1)
Как видно, что система уравнений (1) имеет не сложное решение,
если вид эмпирической функции представляет собой линейную зависимость (
). То есть, если 
,то система уравнений (1) имеет вид
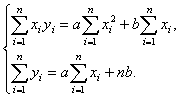(2)
Значит, если эмпирическая функция не является линейной зависимостью, то для
удобного использования метода наименьших квадратов, необходимо свести к
линейной зависимости. Рассмотрим,
как нелинейные зависимости преобразованием координат можно свести к линейной [6].
1
Для показательной зависимости вида 
, логарифмируя имеем 
.
Полагаем lgy=z, x=q, 
, 
и в плоскости qOz получим уравнение прямой z=Aq+B.
Следовательно, система уравнений (2) примет вид
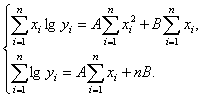
2
Для дробно-рациональной функции
, введем новые переменные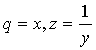 
; тогда получим зависимость вида
Следовательно, система уравнений (2) примет вид
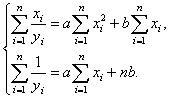
3
Для логарифмической
функции 
; введем новые переменные 
; тогда получим зависимость вида 
4
Для степенной функции 
; введем новые переменные 
; тогда получим зависимость вида
5
Для гиперболической функции 
, введем новые переменные 
; тогда получим зависимость вида 
Для
дробно-рациональной функции 
, введем новые переменные 
; тогда получим зависимость вида
Литература:
1 Демидович
Б.П., Марон И.А. Основы вычислительной математики. - Москва: Наука, 1970. - 664
с.
2
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. – Москва:
Наука, 1996. - 265 с.
3
Джонс Дж.К. Методы проектирования. - Москва: МИР, 1986. - 326 c.
4 Карасев А.И., Кремер Н.Ш.,
Савельева Т.И. Математические
методы и модели в планировании. – Москва: Экономика, 1987. 241 с.
5
Калиткин Н.П. Численные методы. - Москва: Наука, 1978. - 221 с.
6
Березин И.С., Жидков Н.П. Методы вычислений часть I,II.
- Москва: Наука, 1978. - 63 с.
7
Данилина Н.И., Дубровская Н.С., Кваша О.П., Смирнов Г.Л., Феклисов Г.И.
Численные методы. Учебник для техникумов. - Москва: Высшая школа, 1976. - 368
с.
8
Бахвалов Н.С. Численные методы. часть I,II.
- Москва: Наука, 1973. - 256 с
9
Боглаев Ю.П. Вычислительная математика и программирование. - Москва: Наука,
1990. - 315 с.
10
Хемминг Р.В. Численные методы. - Москва: Наука, 1972 – 256 с
11
Заварыкин В.М, Житомирский В.Г, Лапчик М.П. Численные методы. – Москва: МИР,
1991 – 267 с.
12
Воеводин В.В. Численные методы алгебры. – Москва: Наука, 1996 – 134 с.
13
Додж М.и
др. Эффективная работа с EXCEL 7.0. -
Питер: МИР, 1996. – 254 с
14
Новиков Ф., Яценко А. Microsoft Office в целом. – Санкт-Питербург: BHV, 1996. –
267 с.