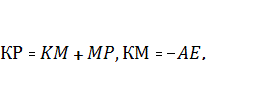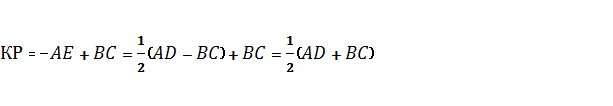Ахмедов Нурлыбек Каштаевич

Ахмедов Нурлыбек Каштаевич

Математика пәні мүғалімі

Қазақстан республикасы, Қызылорда қаласы,

№264 мектеп-лицей

Математикалық ұғымдарды қалыптастыруда, теоремаларды дәлелдеуде аналогия әдісін қолдану

Есеп шығарудың математиканы оқып үйренуде алатын орны өте зор. Оқушылардың математиканы меңгеру деңгейі көбінесе олардың математикалық есептерді шығаруға қаншалықты төселгендігі арқылы баяндалады.

Математикалық есеп дегеніміз – математикадағы заңдылықтар, ережелер және әдіс-тәсілдер негізінде оқушылардан ой мен практикалық іс-әрекетті талап ететін және математикалық білімдерді меңгеруге,оларды практикада қолдана білуге дағдыландыру, ойлау қабілетін дамытуға бағытталған ситуация. Математикалық есептерді шығара білуге үйрету және одан әрі оған дағдыландыру – мұғалімдер алдында тұрған өте қиын да жауапты жұмыс. Әр оқушының математикаға деген ұқыптылығы мен зейінділігі түрліше, ал математикалық есептердің саны шексіз көп. Есеп шығаруға үйрету мен дағдыландыру көбіне сыныпта сабақ өту кезінде болатындықтан, барлық оқушыларды есеп шығарудың әдіс-тәсілдерімен қаруландыру керек. Сол әдістердің бірі – аналогия әдісі.

Математикада аналогияның маңызын белгілі поляк математигі Стефан Банахтың мына сөзінен білуге болады: «тұжырымдар арасында аналогияны тапқан адам математик; жақсы математик теориялар арасындағы аналогияны байқаған адам; бірақ аналогияның арасынан аналогияны тапқандарды да елестетуге болады».

Оқыту процесінде аналогия жаңа білімдерді қалыптастыру, бұрын оқытылған материал мен жаңа материал арасындағы байланысты тағайындау, математикалық ұғымдардың қасиеттерін дәлелдеу, алынған білімдерді қолдану және оны практикалық тексеруде тағы да басқа түрде қолданыс табады.

Баяндаманың мақсаты – оқушыларды математикалық есептерді аналогия әдісімен шешуге үйретіп оқытуға арналған.

Математиканы оқыту процесінде аналогияны кеңінен қолдану оқушылардың пәнге деген қызығушылығын тудыруда, зерттеу іс-әрекеттеріне тартуға эффективті әдістерінің бірі болып табылады. Бұдан басқа, аналогияны қолдану оқушыларға оқу материалын жеңіл және нақты түсінуге мүмкіндік береді, себебі белгілі білімдер және біліктер жүйесін белгілі объектіден белгісіз объектігі ойша аудару жиі мүмкіндік береді.

Математиканы оқыту мақсаттарының бірі – оқушыларға саналы, жүйелі және баянды білім беру. Ал, білім объектілер мен құбылыстардың елеулі белгілері мен олардың байланыстары туралы ғылым тағайындайтын ұғымдардан құралады.

Ұғым ақиқат нәрсенің жалпы және елеулі белгілерін ғана бейнелейді. Егер ол болмысты шын бейнелейтін болса, онда ол әрдайым дұрыс болады.

Ұғымның елеулі белгілері деп біртекті нәрселерді басқа нәрселерден айыруға әрқайсысы қажетті және бәрін бірге алғанда жеткілікті белгілердің жиынын айтады. Елеулі белгілер нәрсені сипаттайды және оны танып – білуге мүмкіндік береді.

Мысалы, параллелограмның елеулі белгілері: а) ол төртбұрыш; ә) қарама-қарсы қабырғалары тең; б) қарама-қарсы қабырғалары тең; в)диагональдары қиылысу нүктесінде қақ бөлінеді; г) қарама-қарсы бұрыштары тең.

Алайда, «Параллелограм» ұғымын анықтау үшін көрсетілген белгілердің бәрін бірдей айту міндетті емес, «а» және «ә» белгілеріндегі немесе «а» және «в» белгілерін айту жеткілікті. Сөйтіп, «параллелограммды» басқа фигуралардан айыру үшін жоғарыдағы елеулі белгілердің бәрін түгендемей-ақ, олардың кез келген елеулілерін көрсетумен шектелуге болады.

Ұғымдарды енгізуде қандай реттілікті сақтау керек? Мұндағы ең басты нәрсе ұғымдарды қолдана білу. Ол мынадай ретпен жүзеге асырылады:

1) Оқу курсының кейінгі материалдарын оқып үйренуде;

2) Салалас пәндерді меңгеруде;

3) Күнделікті өмірде, тұрмыста, еңбек іс-әрекетінде қолдану

Егер бастауыш сыныптарда математикалық ұғымдарды баяндау нақтылы-индуктивті болса, ал VII сыныптан бастап абстрактілі – дедуктивтік баяндауға басымдық беріледі, V-VІ сыныптарда индукциядан дедукцияға біртіндеп көшу жүзеге асырылады. Мұнда оқу материалын баяндауда индукция мен дедукция бірі екіншісімен кезекпен алмастырылып отырады.

Мәселен, параллелепипедтің қасиеттерін оқытқанда оның параллелограммен аналогиясын пайдаланса, меңгеру едәуір жеңілдейді.

1. Тік төртбұрыш диагоналінің квадраты оның екі өлшемінің квадраттарының қосындысына тең.

2. Тік төртбұрыштың диагоналдары тең

3. Параллелограмның қарама-қарсы қабырғалары өзара тең кесінділер.

4. Параллелограмның диагоналдары қиылысу нүктесінде қақ бөлінеді және тағы сол сияқты.

1.Тікбұрышты параллепипедтің диагоналдарының квадраты оның үш өлшемінің квадраттарының қосындысына тең.

2.Тікбұрышты параллепипедтің диагоналдары тең.

3. Параллепипедтің қарама-қарсы жақтары өзара тең параллелограмдар.

4. параллелепипедтің диагоналдары қиылысу нүктесінде қақ бөлінеді және тағы сол сияқты.

Аналогияны кейбір теоремаларды дәлелдегенде де қолдануға болады.

Мысалы 1: Теорема

Тең бүйірлі үшбұрыштың табанындағы бұрыштары тең болады.

Дәлелдеу: – катеті мен гипотенузасы бойынша (СD ортақ, АС=BC есеп шарты бойынша) Бұдан

Тең бүйірлі трапецияның табандарындағы бұрыштары тең болатынын дәлелдеңдер.

Дәлелдеуі: - катеті мен гипотенузасы бойынша (

АВхСD болғандықтан және есеп шарты бойынша) Бұдан

демек

Мысалы 2:

Үшбұрыштың орта сызығы туралы теорема:

Үшбұрыштың орта сызығы табанына параллель және оның жартысына тең.

Трапецияның орта сызығы туралы теорема:

Трапецияның орта сызығы табандарына параллель және олардың қосындысының жартысына тең.

Дәлелдеу:

1. үшбұрышының орта сызығы – DE болсын. D нүктесінен АС қабырғасына параллель жүргізейік. Сонда Фалес теоремасы бойынша ол АВ кесіндісін ортасынан қиып өтеді, яғни DE орта сызығын қамтиды.

2. үшбұрышының DK орта сызығын жүргіземіз. Ол АС қабырғасына параллель. АЕАК және DKАЕ болғандықтан АЕDK параллелограмм

3. Параллелограмның қасиеті бойынша ЕD=AK және СD=CB болғандықтан, Фалес теоремасы бойынша АK=KB. Бұдан ЕD=. Теорема дәлелденді.

Дәлелдеу:

1. АВСD трапециясының орта сызығы – КР болсын. ВЕСD жүргізейік. Сонда ЕDCB – параллелограмм. К нүктесінен АD –ге параллель түзу жүргізейік. Фалес теоремасы бойынша ол ВЕ кесіндісін ортасынан қиып өтетін, яғни КМ кесіндісі үшбұрышының орта сызығы. Демек, КМАD

М және Р нүктелері – параллелограмның ВЕ және СD қабырғаларының орталары, яғни МРЕD. Бірақ бір нүктеден түзуге параллель тек бір ғана түзу жүргізуге болады. Олай болса К, М және Р нүктелері АD түзуіне параллель КР түзуінің бойында жатады.

Теорема дәлелденді.

Аналогия әдісі - индукция әдісімен тығыз байланысты, яғни қарапайымнан күрделіге, жекеден жалпыға қарай бағытталған. Мысалы жазықтықтан кеңістікке, шеңберден сфераға, дөңгелектен шарға, квадраттан кубқа, тік төртбұрыштан параллелепипедке, ауданнан көлемге тағы сол сияқты.

Кеңістікте жазықтықтардың параллельдігін түсіндіру үшін аналогия әдісі негізінде, жазықтықтағы түзулердің параллельдігінің анықтамасын, қасиеттерін және белгілерін пайдаланамыз, яғни

1. Параллель түзулердің қасиеті

1) Егер екі түзу параллель болса және олардың бірі үшінші бір түзуді қиып өтсе, онда екіншісі де сол түзуді қиып өтеді.

2) Егер екі түзу параллель болса және олардың бірі үшінші бір түзуге перпендикуляр болса, онда екіншісіде сол түзуге перпендикуляр болады.

3) Егер екі түзу параллель болса және олардың бірі үшінші бір түзумен α бұрышын жасап қиылысатын болса, онда екіншісіде сол түзумен α бұрышын жасап қиылысады.

2.Параллель жазықтықтардың қасиеті

1) Егер екі жазықтық параллель болса және олардың бірі үшінші бір жазықтықты қиып өтсе, онда екіншісі де сол жазықтықты қиып өтеді.

2) Егер екі жазықтық параллель болса және олардың бірі үшінші бір жазықтыққа перпендикуляр болса, онда екіншісіде сол жазықтыққа перпендикуляр болады.

3) Егер екі жазықтық параллель болса және олардың бірі үшінші бір жазықтықпен α бұрышын жасап қиылысатын болса, онда екіншісіде сол жазықтықпен α бұрышын жасап қиылысады.

Заттар арасындағы ұқсастық пен айырмашылықтарды табу ойлауды жоғары деңгейге көтереді; бұрын өзара байланыспаған білімдер жаңа сапаға ие болады; қарастырылып отырған пән тереңірек, нақтырақ болады. Ұғымдарды салыстыру негізінде гипотетикалық тұжырымдар (жорамал тұжырымдар) құрылады, олардың әділдігі кейін тексеріледі. Дербес жағдайда аналогия бойынша жасалған тұжырымдар гипотетикалық тұжырымдар болады. мұндай тұжырымдар құра отырып оқушылар болжам жасап, белгісізді танып үйренеді, қоршаған табиғат құбылыстары мен заттарының логикалық зерттеу дағдыларын меңгереді. Салыстыру логикалық тәсіл сияқты, ойлауды белсенді ететін ұмтылыс; ұғымдарды салыстыру арқылы жаңа ойлардың қалыптасуы басталады.

Аналогия бойынша ой тұжырымдауда ең алдымен индукция пайдаланады, себебі бір заттан екінші затқа өту (үшбұрыштан тетраэдрге, дөңгелектен сфераға) олардың арасында бір жеке қасиеттерді орнатудан тұрады. (қарапайым көпбұрыш, үш ішкі бұрыштың болуы, олардың тең бөлінетін биссектрисасы және т.б.) Сонымен бірге аналогия бойынша тұжырым дедукция мен тығыз байланысты. Аналогия бойынша қорытындының шындығы дедуктивтік дәлелдеумен орнатылады. Аналогиядан шыққан қорытынды индукциядан басталып дедукциямен аяқталады. Аналогияны пайдаланғанда үлкен, күрделі ойлау процесі жүреді, онда анализ және синтез әдістері пайдаланылады.

Қолданылған әдебиеттер

1) Әбілқасымова А.Е., Көбесов А.К., Рахымбек Д., Кенеш Ә.С. Математиканы оқытудың теориясы мен әдістемесі.-Алматы: Білім,1998

2) Бидосов Ә. Математиканы оқыту методикасы (жалпы методика).- Алматы: Мектеп, 1989

3) Уемов А.И Аналогия в практике научного исследования.-М.,Наука.-1970

4) Пойа Д. Как решать задачу.-М.:Учпедгиз, 1959

5) Метельский Н.В. Дидактика математики: общая методика и ее проблемы (Учеб.Пособие для вуза)-2-е. Изд., перераб.- Мн.: Изд-ва БГУ,1982

6) Эрдниев П.М. Преподавания математики в школе. М., «Просвещение», 1978

7) Саяхова Б. Стереометриядағы аналогия /Информатика. Физика. Математика, 2001, №1

8) Жақыпбекова Г. Геометрия сабақтарын аналогия әдісін қолдану /Информатика.Физика.Математика 1996,№6

9) Саранцев Г.И., Лунина Л.С. Обучение методу аналогии/ Математика в школе, 1989, №4

10) Далингер В.А. Об аналогиях в планиметрии и стереометрии/Математика в школе, 1995,№6