Математика / Математическое моделирование

К.ф.-м.н. Наконечная Т.В., к.т.н. Никулин А.В.

Днепропетровский национальный университет им. О. Гончара,

Днепродзержинский государственный технический университет

МОДЕЛИ И РЕАЛИЗАЦИЯ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ

ПО ВЫСШЕЙ МАТЕМАТИКЕ

Введение. Модель и моделирование, ― универсальные понятия, атрибуты одного из наиболее мощных методов познания в любой профессиональной области, познания систем, процессов и явлений. Модели и моделирование объединяют специалистов различных областей, работающих над решением комплексных проблем, независимо от того, где эта модель и результаты моделирования применяются.

У моделей, особенно математических, есть и дидактические аспекты ― развитие когнитивного стиля мышления, позволяющего вникать в структуру и логику моделируемой системы. Построение модели ― системная задача, требующая анализа и синтеза исходных данных, гипотез, теорий, знаний специалистов.

Фундаментальные дисциплины, в частности математика, образуют основу высшего образования инженеров и экономистов. Качество подготовки специалистов зависит от развития их профессиональных и математических компетенций. Предметная область высшей математики характеризуется большими объемами абстрактных сведений с преобладанием многоуровневых зависимостей между объектами (например, использование характеристического уравнения однородной линейной системы алгебраических уравнений при решении линейной системы дифференциальных уравнений). Эффективность освоения и дальнейшего применения математики студентами и, в будущем, специалистами связаны с применением информационно-коммуникационных технологий (ИКТ). В настоящее время происходит повсеместный переход к использованию автоматизированных информационных систем, в том числе и математических [1]. Возникает необходимость в переформатировании методического обеспечения по высшей математике, ориентированного на инновации.

Постановка задачи. Создание и использование полноценных математических систем прямо зависит от эффективной формализации математических знаний и освоения приемов работы с базами знаний [2].

Для выполнения задачи формализации математических знаний (МЗ) вводятся основные понятия и их взаимосвязи, определяющие особенности предметной области высшей математики:

1. Под математическими знаниями понимаются знания о методах и способах представления математических данных, их обработки и анализа полученных результатов. Примером математических знаний служит следующее высказывание (интегральный признак Коши):

Если сходится несобственный интеграл 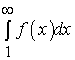, где монотонно убывающая неотрицательная функция , то сходится и числовой ряд , где .

2. Под математическим объектом (МО) понимается любой из объектов, с которым в результате математического оперирования происходит анализ и синтез, приводящие к решению поставленной задачи.

При модернизации учебных пособий, других видов методического обеспечения учебных дисциплин следует использовать результаты формализации математических знаний c учетом модульно-рейтинговой системы организации обучения.

Полученные результаты. Основные компоненты модели МЗ и их взаимодействие представлены схемой (рис. 1). В соответствии с учебными планами многих инженерных и экономических специальностей естественно ограничиться моделью представления знаний по высшей математике.

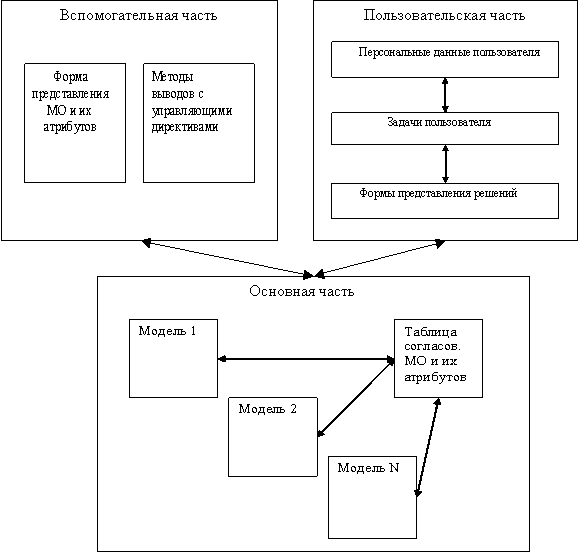
Рис. 1. Основные компоненты модели представления математических знаний

Математические объекты при моделировании определяются рабочими учебными программами: системы линейных алгебраических уравнений, произведения векторов, дифференциальные уравнения и т.д. Каждый из объектов представляет собой систему, так как описываются элементы, из которых она состоит, определяются отношения между ними, правила операций (правила вывода), исследуются свойства, рассматриваются примеры решения типовых задач. В связи с переходом к модульно-рейтинговой системе обучения потребовалось переформатирование известных учебных материалов в соответствии с содержательными модулями действующих программ курса высшей математики, применяемыми математическими системами и системой оценивания.

Реализация моделей математических знаний в обучении производилась параллельно в бумажной и электронной формах.

Подготовлена серия учебных пособий с грифом МОН Украины [3], сборник тестовых материалов [4], справочное пособие [5]. Рассмотрим пример словесно-формульной реализации модели математического объекта «Системы дифференциальных уравнений»[5].

Системи диференціальних рівнянь

Система диференціальних рівнянь (СДР) першого порядку, яка записана в нормальній формі, має вид:

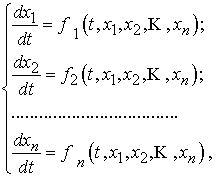
або у скорочену виді: та

векторній формі: 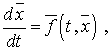де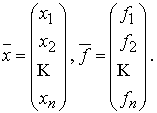

Розв’язком СДР називається сукупність функцій які перетворюють рівняння системи в правильні рівності відносно t .

Загальним розв’язком системи диференціальних рівнянь називається сукупність функцій , які залежать від n довільних сталих та перетворюють рівняння системи в правильні рівності при будь-яких допустимих значеннях сталих .

Частинним розв’язком системи диференціальних рівнянь називається розв’язок, який задовольняє заданим початковим умовам

Досить часто СДР розв’язують методом виключення змінної. Згідно з ним диференціюємо рівняння даної системи та виконуємо підстановки. В результаті одержимо рівняння n-го порядку, наприклад, відносно функції :

Нехай ― розв’язок цього рівняння. Після послідовного диференціювання розв’язку та підстановок дістанемо загальний розв’язок системи

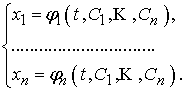
Приклад розв’язання завдання

Задача. Розв’язати задачу Коші для системи лінійних диференціальних рівнянь , .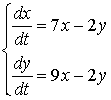

Розв’язання. Виразимо з першого рівняння системи функцію через та . Знайдемо першу похідну від функції та підставимо отримані вирази у друге рівняння. Маємо . Тоді

.

Розв’язуючи отримане лінійне диференціальне рівняння дістаємо, що

.

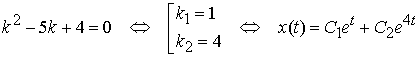Отже, ми можемо знайти функцію :

.

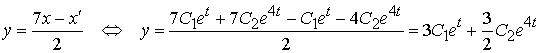Таким чином ми отримали загальний розв’язок системи диференціальних рівнянь 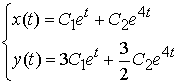. Застосовуючи початкові умови, ми отримуємо лінійну систему для знаходження невідомих сталих: .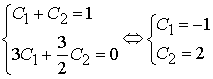

Отже, частинний розв’язок системи диференціальних рівнянь має вигляд:

.

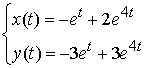Відповідь: .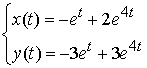

Как пример использования математических систем при решении систем дифференциальных уравнений, приведем решение данной системы с привлечением математического пакета Maple 10.

> sys_ode:=diff(x(t),t)=7*x(t)-2*y(t),diff(y(t),t)=9*x(t)-2*y(t);

> dsolve([sys_ode]);

> ics:=x(0)=1,y(0)=0;

> dsolve([sys_ode,ics]);

На информационном портале ДГТУ имеется электронная версия пособия [5]. В свободном доступе можно воспользоваться не только МО «Системы дифференциальных уравнений», но и другими МО, соответствующими нормативным знаниям по высшей математике для семи разделов курса. Как и другое методическое обеспечение, реализованные модели математических знаний можно найти по адресу [6].

Выводы. Разработка и совершенствование моделей представления математических знаний – актуальное направление повышения эффективности автоматизации в интеллектуальной деятельности студентов, будущих инженеров и экономистов.

Неотъемлемый этап моделирования ― определение атрибутов математических объектов, необходимого и достаточного для формирования решений. Для представления математических знаний возможно использование методологии структурного анализа.

С учетом имеющихся технических возможностей модели математических знаний реализуются в бумажной форме в виде учебных пособий, другого методического обеспечения процесса обучения, а также в электронной форме в виде электронных пособий, методического обеспечения на сайтах информационных порталов университетов.

Библиографические ссылки

1.Кондаков А.И. Унификация моделей представления технологических знаний / А.И. Кондаков, А.В. Туликов // Вестник компьютерных и информационных технологий. – 2006, №9. – С. 29 – 33.

2.Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.: Мир, 1976. – 77с.

3.Вища математика для підготовки бакалаврів з інженерії: Навч. посібник: У 3 Ч. / А.П. Огурцов, Т.В. Наконечна, О.В. Нікулін; за заг. ред. А.П. Огурцова . – Дніпродзержинськ.: ДДТУ, 2008. – Ч. 1. – 428 с.; Ч. 2. – 340 с.; Ч. 3. – 320 с.

4.Шумейко О.О. Модульне і підсумкове оцінювання: тести з вищої математики: Навч. посіб./ О.О. Шумейко, Т.В. Наконечна, О.В. Нікулін. – Дніпропетровськ: «Наука і освіта», 2009. – 172 с.

5. Нікулін О.В. Вища математика: факти і формули, задачі і тести: Навч. посіб./ О.В. Нікулін, Т.В. Наконечна. – Дніпропетровськ : Біла К.О., 2015. – 188 с.

6. Кафедра вищої математики. Доцент, к.т.н. Нікулін О.В. Електронний ресурс [http://www.dstu.dp.ua:8080/Portal/WWW/autor.php?id_prep=137&id_dep=21]