Сатыбалдиев О.С. п.ғ.д., профессор, Жансейітова Л. магистрант

Қ.И.Сәтбаев атындағы ҚазҰЗТУ , Алматы қ., Қазақстан Республикасы

Бәсекелестіктің математикалық моделі

Қандайда бір территорияда өмір сүруші екі биологиялық түрді қарастыралық. Бұл екі түрдің бір біріне тікелей әсері бар. Бұл екі түр бір азықпен қоректенетіндіктен бір бірімен бәсекеге түседі.

Осы қарастырылып отырған процестің математикалық моделін құралық. Айталық, ші биологиялық түрдің саны болсын. Оның өзгеру жылдамдығы қарастырылып отырған түрдің санына пропорционал, яғни болады. Мұндағы -ші биологиялық түрдің өсу саны, . Азық жеткілікті жағдайда бұл түрлердің арасында бәсекелестік болмайды, ал олардың өсу саны табиғи өсуімен сәйкес келеді. Азықтың шектелуіне байланысты түрлердің саябырлай бастайды. Осы айтқандарды ескерсек теңдеуін аламыз. Мұндағы -қажетті азық саны; ші түрдің өсуі; ші түрдің алу саны; ші түрдің қоректенетін азық саны .

Сөйтіп, қарастырылып отырған процесс төмендегі дифференциалдық теңдеулер жүйесімен сипатталады

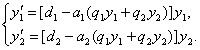(1)

Мұндағы -ші түрдің қарқынды өсуі. (1) қатынас бәсекелестік теңдеулері деп аталады.

Уақыттың бастапқы мерзімінде ші түрдің саны белгілі және ол - ға тең деп ұйғаралық, яғни

(2)

бастапқы шарты орындалсын. (2) бастапқы шарт және дифференциалдық теңдеулер жүйесі қарастырылып отырған процестің математикалық моделін береді. (1) теңдеудің сызықтық еместігіне байланысты оның шешімін табу қиындыққа әкеледі. Сондықтан, біз, құрылған моделді зерттеудің жалпы жолын іздеуге тырысамыз. (1) жүйеден

өрнегін аламыз. Осыдан

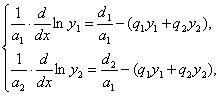
теңдіктерін аламыз. Осы теңдіктердің біріншісінен екіншісін шегеріп 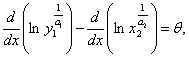теңдігін аламыз. Мұндағы .

Сөйтіп, біз, (1) теңдеуді шешуде негізгі қиыншылықты тудыратын оның сызықтық емес мүшесінен құтылдық. Жоғарыда алынған теңдікті мына түрде жазалық

.

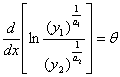Осы өрнектің екі жағын интегралдап және (2) бастапқы шартты ескере отырып

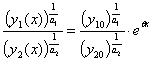(3)

теңдігін аламыз. болсын ұйғаралық. Бұл жорамалымыздың жалпы жағдай үшін кедергісі жоқ, себебі алғашқы биологиялық түр үшін біз қатынасы төмен болатындай етіп таңдауға құқылымыз.Әртүрлі биологиялық түрлер үшін бұл қатынастардың бір бірімен сәйкес келуі күмәнді, сондықтан ол практикалық тұрғыдан қызығушылық тудырмайды бұл жағдайда (3) теңдіктің сол жағы уақыт бойынша өзгермейді. Олай болса (3) қатынастан шекке көшіп

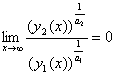(4)

теңдігін аламыз. (4) шарт не бірінші биологиялық түрдің саны шексіз өскенде, не екінші биологиялық түрдің нөлге ұмтылғанда жүзеге асады. Алайда, мына мәселені ескеру қажет: функциясы өскенде белгілі бір уақыттан бастап теңсіздігі орындалады. Сондықтан (2) теңдікке сәйкес бірінші биологиялық түрдің саны азая бастайды. Демек, бұл модель бойынша функцияның шексіз өседі болжамды теріске шығарады. Демек, (4) теңдік биологиялық түрдің саны нөлге ұмтылғанда ғана орындалады.

Енді уақыттың өзгеруіне қарай бірінші биологиялық түр санының өзгеруін қарастыралық функциясы шексіздікке ұмтылғанда нөлге ұмтылады, яғни уақыт өткен сайын сол территорияда тек қана бірінші биологиялық түр қалады. Онда өте үлкен дәлдікпен, алда қарастырылған (3) қатынаспен пара-пар теңдеуін аламыз. Жоғарыдағы пайымдауларды қайталай отырып, уақыт өткен сайын бұл жүйе тепе-теңдік қалпына ұмтылатындығына көз жеткіземіз. Бастапқы мезгілдегі биологиялық түрлердің сандары аз болған жағдай қиын емес, бұл қарастырылып отырған жүйенің сапалық көрсеткіші.

Сөйтіп, екі биологиялық түрдің өміршеңдігі бірдей анықталған жағдайда олардың ешқайсысы жойылып кетпейді және олардың саны сол түрді сақтап қалу мүмкіндіктеріне сәйкес белгілі бір сандық мәнге ие болады екен.Биологиялық түрдің бірін бірі ығыстыру жағдайы болмайды, себебі бұл жағдайда популяциялар біртекті болады, яғни екі биологиялық түр тұтас түр ретінде сақталынады. Егер бастапқыда бір биологиялық түрдің саны басымдау болып ол басымдылық біраз уақыт сақталынады. Сонымен, бұл жағдайда оқиғалар дамуының бір ғана нәтижесі емес, тепе-теңдік жағдайдың тұтас жиыны орын алады, екен, тепе теңдік жағдайды нақты жүзеге асыру жүйенің бастапқы жағдайымен айқындалады.

Пайдаланылған әдебиеттер

1. Абатуров Б.Д., Лопатин В.Н., Связь уровня потребления пищи с размерами тела у растительноядных млекопитающих// Журн. общ. биологии. 2010. Т.48, №6. С. 763-770.

2. Викторов Г.А., Колебания численности насекомых как регулируемый процесс// Журн. общ. биологии. 2011. Т.26, №1. С.43-55.

3. Винберг Г.Г., Многообразие и единство жизненных явлений и количественные методы в биологии// Журн. общ. биологии. 2013. Т.42, №1.С.5-18.