Сатыбалдиев О.С. п.ғ.д., профессор.

Нөкеев Ә.Қ., Албан Асан атындағы орта мектеп директоры

Қ.И.Сәтбаев атындағы ҚазҰЗТУ , Алматы қ., Қазақстан Республикасы

Математикалық модельдердің оқушылардың

нақты дүниені танудағы рөлі

Мектепте көңіл аударарлық факторларының бірі оқушыларға математикалық модельдерді үйрету. Бұл оқушылардың диалектикалық дүние танымына тікелей әсер етеді, өйткені үлгілер - нақты дүниені танудың жалпы ғылыми әдісі. Математикалық модельдердің негізін меңгеру қазіргі кезеңде аса маңызды болып отыр. Сондықтан оқушыларға математикалық модельдерді құру мен зерттеуге баулитын әдістерді үйрету мектеп мұғалімдерінің негізгі міндеті болып табылады.

Математикалық моделдеу бір-біріне сорпасы қосылмайтын екі дүниені, яғни жеке ғылымдардың көмегімен зерттелетін бізді қоршаған шындық дүние мен математиканың заңдары үстемдік ететін абстрактылы дүниені қосатын алып көпір.

Осы жоғарыда айтылған мәселелерге сәйкес нақты мысалдарға жүгінелік.

1. Айталық қандайда бір өндіріс орынының 50 және 60 бірліктерді құрайтын екі түрлі қоры бар болсын. Олар екі түрлі өнім өндірсін. Әрбір дайын өнімнің бағасы сәйкес 3 және 4 теңге болсын. Бірінші өнімді дайындауға бірінші қордың 2 бірлігі, ал екінші қордың 3 бірлігі жұмсалсын. Екінші өнімді дайындауға бірінші қордың 4 бірлігі, екінші қордың 2 бірлігі кетсін. Осы өндіріс орнының дайындаған өнімдерінен түскен пайда ең көп болатындай тиімді жоспар жасау қажет.

Осы есептің математикалық моделін құралық. және арқылы сәйкес бірінші және екінші дайын өнімдердің санын белгілейік. Бұл өнімдерді сатудан түсетін өндірістің жалпы пайдасы болады. пен айнымалыларына келесі шектеулер қойылады:

1) (бұл барлық өнімдерді дайындауға жұмсалатын бірінші қордың шығыны қолда бар барлық қордан асуы мүмкін емес дегенді білдіреді).

2) (бұл да солай).

3) және (бұл бірінші және екінші бар барлық қордан асуы мүмкін емес дегенді білдіреді).

Осы айтылғандарды сарай келе қарастырылып отырған есептің төмендегідей математикалық моделін аламыз:

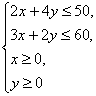
Олай болса осы шарттарды қанағаттандыратын функциясының ең үлкен мәнін табу керек.

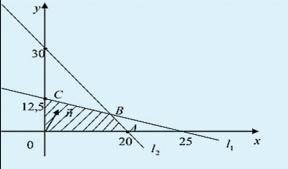
жазықтығында жоғарыдағы шарттарды қанағаттандыратын жүйенің шешімдерінің облысын құрлық (1-сурет).

Cуретте , түзуі теңдеуіне, түзуі теңдеуіне, түзуі түзуіне және түзуі теңдеуіне сәйкес келеді. Осы төрт түзумен қоршалған төртбұрышы берілген жүйенің шешімін береді. векторы функциясының өсу бағытын көрсетеді.

Осы өсу бағыты бойынша облысының соңғы нүктесі нүктесіне сәйкес келеді. Бұл деп отырғанымыз функциясы өзінің ең үлкен мәнін осы нүктесінде қабылдайды деген сөз. нүктесіне жүйенің тиімді шешімі сәйкес келеді, себебі нүктесіне жүйенің тиімді шешімі сәйкес келеді, себебі ол бұрыштық нүкте.

1-сурет

нүктесінің координаталарын

жүйесін шешу арқылы табамыз, яғни Сонымен, функциясы өзінің ең үлкен мәнін (17,5; 3,75) нүктесін қабылдайды және ол мән 67,5 санына тең.

2. Ара қашықтығы 200 шақырымға тең мен екі өнеркәсіптің шығаратын өніміне заводтың қоятын бағасы (теңге) екі өнеркәсіп үшін де бірдей. Өнеркәсіп -дан тұтынушы -ға дейін бірлік өнімді тасымалдап жеткізу шығыны 9 теңге/км болса, өнеркәсіп -дан – жеткізу шығыны 3 теңге/км. Тұтынушылардың жұмсайтын қаржысы бірдей болса, өтім базары қалай бөлінуі тиіс? Қай тұтынушы қай өнеркәсіптің бұйымын сатып алғаны тиімді?

Тікбұрышты координаттар жүйесін алып, бас нүктені кесіндісінің ортасынан белгілеп алып және де координаттар өстерін сәулесі бойымен және оған перпендикуляр бағыттайық (2-сурет). Айталық, тұтынушы нүктесінде орналасқан болсын. Ара қашықтықтарды былай белгілеп аламыз. (км), (км).

2-сурет

Сонда кәсіпорнының бірлік өнімін сатып алуға жұмсалатын қаражат болса, ал кәсіпорыны үшін . Тұтынушылардың жұмсайтын қаржылары бірдей болатындықтан, немесе . Нүктелердің координаттарын және пайдаланып, мыналарды есептеп шығарайық:

,

және оларды теңдіктегі орындарына қояйық, сонда

.

Бұдан шығатын теңдеу немесе . Осы теңдеудің екі жақ бөлігін де 8-ге бөліп, содан кейін оның сол жақ бөлігінде толық квадрат бөліп шығарайық, сонда , немесе , немесе

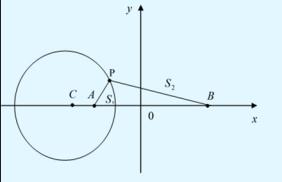
Соңғы теңдеу – центрі нүктесінде және радиусі болатын шеңбердің теңдеуі болып табылады (6-сурет). Осы шеңбермен шектелген аймақта тұратын тұтынушылар үшін , олай болса, ; сондықтан өнеркәсібінің бұйымы арзандау түседі. Осы сияқты, айтылған дөңгелектен тысқары орналасқан тұтынушылар үшін өнеркәсібінің бұйымы арзан түседі. Сонымен өтім рыногін былай бөлу тиімді:

а) шеңбер бойында орналасқан тұтынушылар үшін екі өнеркәсіптің ( мен ) әрқайсысының бұйымы да бірдей түседі;

б) сол дөңгелектің ішінде орналасқан тұтынушылар өнеркәсібінің бұйымын сатып алады;

в) дөңгелектен тысқары орналасқан тұтынушылар өнеркәсібінің бұйымын сатып алады.

Қазіргі мезгілдегі орта мектепте пайдаланып жүрген математиканың бағдарламалары мен оқу құралдары оқушылардың математикалық дайындықтарына қойылатын талаптарына сәйкес іскерліктері мен дағдыларын бөліп алуға мүмкіндік береді. Оқушылар интегралдар бойынша келесі іскерліктер мен дағдыларды білулері тиіс: функциялардың алғашқы функцияларын, интегралдың көмегі арқылы қисық сызықты трапецияның ауданын, денелердің көлемін таба білу; интегралдарды басқа ғылымдарда (физика, химия, биология т.б.) және практикада қолдана білу.

3. функциясы еңбек өнімділігінің өзгерісін сипаттайды делік ( - жұмыс күні басталған мезеттен бастап саналатын уақыт аралығы). Жұмыс күнінің соңғы сағатында өндірілетін өнім мөлшерін анықтау керек (жұмыс күні сегіз сағат).

Өнім мөлшерін [7;8] кесіндісі нүктелерімен бөлінген өте аз уақыт интервалында өндірілген өнім мөлшерінің қосындысы ретінде қарастыруға болады. Сонда осындай ұзындығы өте аз интервалдардың қай - қайсысында да функциясы өзгермейді деп санауға болады, ал олай болса, өндірілген өнім мөлшері еңбек өнімділігі мен уақыттың көбейтіндісіне тең. Сонда жұмыс уақытының соңғы сағатында өндірілген өнім төмендегідей анықталады:

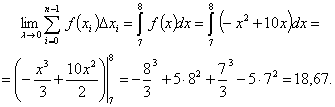
Олай болса, соңғы жұмыс сағатында 18,67 (шартты бірл.) өнім өндірілген.

4.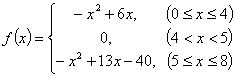 функциясы еңбек өнімділігін сипаттайды делік, - жұмыс күні басталғаннан саналатын уақыт. Бүкіл жұмыс күні өндірілген өнім мөлшерін анықтау керек.

Өндірілген өнім мөлшерін түске дейінгі 4 сағатта және қалған жұмыс күнінің 3 сағатында өндірілген өнім мөлшерінің қосындысы ретінде қарастыруға болады. Алдыңғы есептің шығару жолына қарап, өндірілген бүкіл өнімнің мөлшері анықталған екі интегралдың қосындысы екенін көрсету қиын емес:

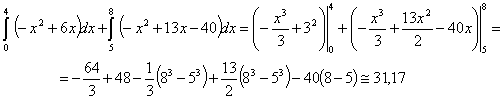
(шартты бірл.).

5. функциясы электростанцияға түскен жүктеме (квт. сағат есебімен) делік ( - тәуелділіктің басынан саналатын сағат саны; ). Тәулік бойы жұмсалатын электр қуатының мөлшерін есептеу керек.

Тәулік бойы пайдаланылатын электр қуаты [0;24] кесіндісі нүктелерімен бөлінген өте аз уақыт интервалдарында пайдаланылған электр қуаты мөлшерінің қосындысы ретінде өрнектеуге болады. Ал ұзындығы болатын өте аз интервалдардың әрқайсысында функциясы өзгермейді деп санауға болады. Сонда уақыт аралығында пайдаланылған электр қуатын көбейтіндісі өрнектесе, ал тәулік ішінде пайдаланылған электр қуаты интеграл арқылы анықталады:

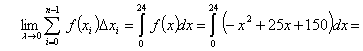
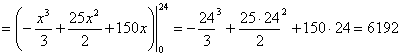(квт.сағ)

6. функциясы қоймаға товар түсе бастаған мерзімнен бастап санағанда (сағат есебімен) уақыт ішінде дүкен қоймасына түскен товар (шартты бірлік есебімен) мөлшері болсын. 3 сағаттан кейін қоймаға түскен товар қорын есептеу керек.

Жалпы жағдайда уақыт ішінде қоймаға бірлік товар түседі. Олай болса, товар қабылданған мерзімнен бастап (егер товар қоймаға үздіксіз түсетін болса), қойманың қорлануы

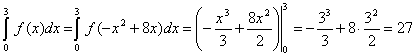(бірл.товар).

Пайдаланылған әдебиеттер

1. Сатыбалдиев О.С., Мордкович А.Г. Алгебра и начала математического анализа. –М.: Учебник 10кл., ООО «ИОЦ Мнемозин», Москва 2014г. - 298стр.

2. Сатыбалдиев О.С., Мордкович А.Г. Алгебра и начала математического анализа. –М.: Задачник 10кл., ООО «ИОЦ Мнемозин», Москва 2014г. - 202стр.

3. Сатыбалдиев О.С., Мордкович А.Г. Алгебра и начала математического анализа. –М.: Учебник 11кл., ООО «ИОЦ Мнемозин», Москва 2014г. - 238стр.

4. Сатыбалдиев О.С., Мордкович А.Г. Алгебра и начала математического анализа. –М.: Задачник 11кл., ООО «ИОЦ Мнемозин», Москва 2014г. - 167стр.