Математика/5.
Математическое моделирование
К. п. н. Коробская А. В.
Харьковский национальный университет имени В. Н. Каразина,
Украина
Об операторе двойного интегрирования
Теория
модельных представлений несамосопряженных операторов является развивающимся направлением
функционального анализа. Первые фундаментальные исследования в этом направлении
были получены в работах М. С. Лившица [1] по теории
характеристических функций, что дало предпосылки к появлению работ по теории
спектральных представлений несамосопряженных и неунитарных операторов [2],
треугольных и жордановых представлений линейных операторов [3], операторов в
гильбертовом пространстве [4]. Для несамосопряженных операторов аналогом
спектральных разложений являются треугольные модели. Отметим, что оператор
двойного интегрирования, представленный в работе, в данном аспекте не изучался.
Рассмотрим
оператор двойного интегрирования вида ![]() :
: ![]() , где
, где ![]() ,
, ![]() ,
, 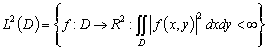 ,
,
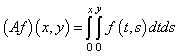 . (1)
. (1)
Сопряженный оператор к оператору (1) ![]() будет иметь вид:
будет иметь вид:
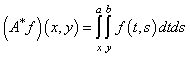 .
.
Включим оператор ![]() в узел, т. к.
в узел, т. к. ![]() – линейный,
ограниченный оператор. В нашем случае
– линейный,
ограниченный оператор. В нашем случае ![]() . Построим гильбертово пространство
. Построим гильбертово пространство ![]() . Вычислим
. Вычислим ![]() . Обозначим
. Обозначим ![]() . Найдем замыкание образа оператора
. Найдем замыкание образа оператора ![]() .
.
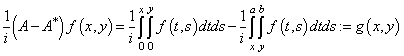 .
.
Тогда
![]() . (2)
. (2)
Из (2) следует, что ![]() . Значит,
. Значит, 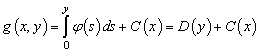 .
.
Итак, пространство ![]() имеет вид:
имеет вид:
![]() , (3)
, (3)
и его можно представить как ортогональную сумму ![]() , где
, где 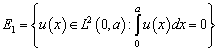 ,
, 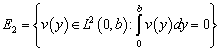 ,
, ![]() .
.
Возьмем ![]() ,
, ![]() . Введем в
. Введем в ![]() (3) скалярное
произведение для
(3) скалярное
произведение для ![]() и
и ![]() :
:
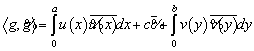 ,
, 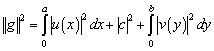 .
.
Очевидно, что пространство ![]() является гильбертовым
пространством.
является гильбертовым
пространством.
Определим оператор ![]() , причем
, причем ![]() . Для этого зададим ортопроекторы
. Для этого зададим ортопроекторы ![]() ,
, ![]() такие, что:
такие, что:
![]()
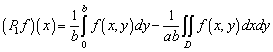 , (4)
, (4)
![]()
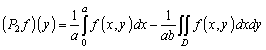 , (5)
, (5)
![]()
![]() . (6)
. (6)
Можно доказать, что ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Определим ортопроектор
![]() , (7)
, (7)
где ![]() , , а
, , а ![]() ,
, ![]() ,
, ![]() имеют вид (4), (6),
(5), соответственно.
имеют вид (4), (6),
(5), соответственно.
Найдем ![]() такое, что
такое, что ![]() ,
, 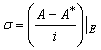 . Для
. Для ![]() и любых функций
выполнено
и любых функций
выполнено ![]()
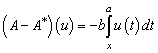 ,
, ![]()
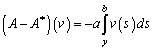 . Подействовав на полученные функции оператором
. Подействовав на полученные функции оператором ![]() (7), получим, что имеет
место следующая лемма.
(7), получим, что имеет
место следующая лемма.
Лемма. Если ![]() в
в ![]() имеет вид:
имеет вид:
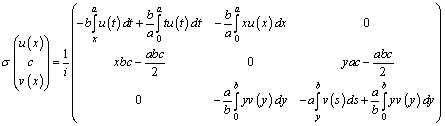 , (8)
, (8)
то
выполняется узловое соотношение:
![]() ,
,
где
оператор ![]() определен формулой
(1), а оператор
определен формулой
(1), а оператор ![]() равен (7).
равен (7).
Итак, построили оператор ![]() . Нами доказана следующая теорема.
. Нами доказана следующая теорема.
Теорема. Совокупность ![]() образует узел, где
образует узел, где ![]() определяется условием
(1),
определяется условием
(1), ![]() – условием (7),
– условием (7), ![]() – условием (3),
– условием (3), ![]() – условием (8).
– условием (8).
Таким образом, в данной
работе изучен оператор двойного интегрирования, который действует в пространстве
![]() , где
, где ![]() . Осуществлено включение данного оператора в узел и описаны
параметры узла.
. Осуществлено включение данного оператора в узел и описаны
параметры узла.
Литература:
1. Лившиц М. С. Теория операторных
узлов в гильбертовых пространствах / М. С. Лившиц,
А. А. Янцевич. – Х. : Изд-во Харьк. ун-та, 1971. – 160 с.
2. Золотарев В. А.
Аналитические
методы спектральных представлений несамосопряженных и неунитарных операторов / В. А. Золотарев. – Х.
: [ХНУ], 2003. – 342 с.
3. Бродский М. С. Треугольные и жордановы
представления линейных операторов / Бродский М. С.
– М. : Наука, 1969. – 287 с.
4. Надь Б. С. Гармонический анализ
операторов в гильбертовом пространстве / Б. С. Надь,
Ч. Фояш. – М. : Мир, 1970. – 431 с.