УДК 54-142

Вязкость жидких металлов по концепции хаотизированных частиц

Кажикенова А.Ш., Макашева А.М., Алибиев Д.Б.

Как известно, жидкое состояние вещества является наиболее сложным для теоретического описания. В структуре жидкости пространственное расположение атомов не закреплено, как в кристалле, но и не находятся в свободном состоянии, как в газе. Поэтому жидкость по своим свойствам может приближаться к газу вблизи температуры кипения или к твердому телу вблизи температуры плавления.

Так, основная характеристика жидкости – вязкость – не поддается строгому теоретическому выражению на основании различного учета сил связи частиц, то есть структурных факторов, и авторы [1], осуществившие систематический анализ теоретических и экспериментальных работ по вязкости жидких металлов, приходят к выводу, что единственно достаточно достоверным источником сведений о вязкости жидких металлов при различных температурах является эксперимент, аналитическое описание которого возможно либо статистическими аппроксимирующими моделями, либо полуэмпирическими моделями с двумя и более подгоночными параметрами. Свойства жидких металлов получены в основном из экспериментальных исследований.

Сотрудниками Химико-металлургического института (г. Караганда) была разработана модель температурной зависимости вязкости металлов, основанная на концепции хаотизированных частиц [2]. Согласно концепции, три агрегатных состояния вещества рассматриваются с единой точки зрения по его бесструктурной составляющей, которая численно определяется долей сверхбарьерных и подбарьерных по теплосодержанию в точках плавления RT_m и кипения RT_b частиц согласно распределению Больцмана. Предложенная авторами концепции базовая модель кинематической вязкости определяется влиянием на эту характеристику кристаллоподвижных частиц

, (1)

где в качестве реперной можно использовать не только точку плавления T_m, но и любую другую надежно определенную величину вязкости n_r при T_r.

Представляет также интерес рассмотреть обоснование вывода температурной зависимости кинематической вязкости с независимым учетом еще одной индивидуальной характеристики вещества, т.е. в качестве энергетического барьера рассматривать не теплосодержание, а теплоту плавления DH_m.

Интервал относительного изменения кинематической вязкости от n_m при температуре плавления T_m до n = 0 при бесконечно высокой температуре (где жидкость может существовать в закритической области температуры и давления в неразличимом с газом состоянии) выразится как

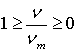. (2)

В этом же интервале температур доля кристаллоподвижных частиц, изменяется в пределах

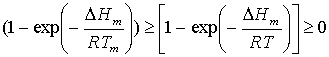. (3)

Раскрывая скобки и алгебраически преобразуя это неравенство, получим

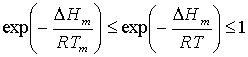. (4)

После логарифмирования результат тождественных преобразований исходного неравенства (3) примет вид

, (5)

полностью совпадающий с пределами относительных изменений вязкости (2).

Постулируя прямую корреляцию относительных изменений вязкости и обратной относительной температуры, которая учитывает изменение в нормированном виде доли кристаллоподвижных частиц,

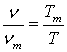, (6)

находим расчетную формулу для кинематической вязкости

, (7)

которое полностью идентично уравнению (1), выведенному в [2]. Как и в уравнении (1), в качестве реперной можно использовать не только точку плавления

. (8)

Таким образом, можно сделать следующие выводы:

1. На основе концепции хаотизированных частиц получено дополнительное обоснование вывода базовой модели кинематической вязкости с независимым учетом еще одной индивидуальной характеристики вещества.

2. Показано, что нормировка уравнения для доли кристаллоподвижных частиц по теплоте плавления или любой другой энергетической характеристике приводят к одной и той же модели вязкости (1), чем обосновывается ее базовое значение.

Список использованных источников

1 Шпильрайн Э.Э., Фомин В.А., Сковородько С.Н., Сокол Т.Ф. Исследование вязкости жидких металлов. – М.: Наука, 1983. – 244 с.

2 Малышев В.П., Турдукожаева А.М., Кажикенова А.Ш. Вязкость расплавов металлов по концепции хаотизированных частиц // Тяжелое машиностроение. – 2009. – № 6. – С. 37-39.