Математика/4. Прикладная математика

Абденова Д.М., Искакова А.С.

Евразийский национальный университет имени Л.Н. Гумилева, Астана, Казахстан

Многомерное обобщенное показательное распределение вероятностей, порождаемое суммами случайных величин

Одной из характерных особенностей работы дистанционного зондирования Земли — наблюдение поверхности Земли.

Дистанционное зондирование можно представить как процесс, посредством которого собирается информация.

На энергетические характеристики радиолинии передачи данных в режиме HR с ИСЗ Meteosat серии МОР /22/ (см. [1], стр. 205) влияют ЭИИМ, потери на распространение, потери на наведение антенны (), КНД приемной антенны с диаметром зеркала 4 м, потери в фидерных линиях, потери на отражение, принимаемая мощность , модуляционные потери, эффективный принимаемый сигнал , шумовая температура антенны для угла места 30°, шумовая температура РПУ, шумовая температура системы , спектральная плотность шума , скорость передачи информации 166 кбит/с, общая мощность шума , отношение с/ш (9-15), потери демодулятора, эффективное отношение с/ш , требуемое отношение с/ш для вероятности ошибки, запас мощности для вероятности ошибки, добротность системы () . Иными словами на искажение влияют 23 фактора, то есть d=23.

Рассмотрим вероятностную модель процессов энергетических характеристик радиолинии ИСЗ Meteosat. В работе [2] приведена вероятностно-статистическая вероятность оправдываемости метеорологического прогноза. Также ранее в работах [3-4] были исследованы вероятностные распределения ошибок снимков дистанционного зондирования, имеющие обобщено полиномиальное распределение. Однако, дискретные распределения довольно не удобны в техническом использовании и не учитывают специфику поточных случаев.

Допустим, что истинное изображение представимо в виде величины l₀, на которые наложили искажения u, состоящее их d факторов, принимающие значения из множества L₁,.., L_d, причем L₁,.., L_d –независимые случайные величины, подчиняющие показательному распределению соответствующими параметрами λ₁,.., λ_d.

Допустим, что V_u представляет число возможных сочетаний _, которые в сумме образовали u, где определяют возможное количество соответствующих факторов . Иначе говоря, из работ [2-4] следует, что V_u есть число разбиений на части .

Теорема. Вероятность искажения значения u определяется по формуле

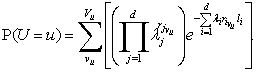(1)

Доказательство. Пусть – есть пространство элементарных исходов представленной модели и

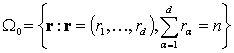
есть пространство элементарных исходов обобщенного показательного распределения, имеющий вид

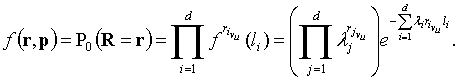
Рассмотрим следующую сумму

Разумеется, что, если имеет место разбиения на , то разбиение происходит V_u≥1 способами. Для каждого способа разбиения имеем вектор

.

Также очевидно, что является решением системы уравнений

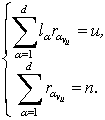(2)

Из чего следует, что вектор соответствует только одному определенному . Следовательно, если и , то при любых и . Таким образом, имеем

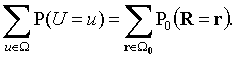
Поэтому

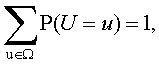
и, следовательно, рассматриваемый способ задания вероятностей по формуле (1) является корректным.

Теорема доказана.

Пример. Допустим, что где α принимает любые натуральные числа на промежутке от 1 до d=5. Для n=3 определим вероятность P(U=4).

Решая систему уравнений (2) с использованием имеющихся данных, получаем два разбиения u на l₁,…, l₅

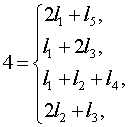
или

Таким образом, вероятность того, что случайная величина U примет значение u, есть

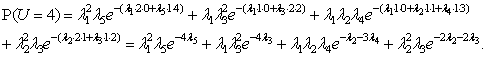
Литература:

1. С.В.Гарбук, В.Е.Гершензон. Космические системы дистанционного зондирования земли. МОСКВА, 1997, 297 с.

2. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84.

3. Ayman I. Construction of the most suitable unbiased estimate distortions of radiation processes from remote sensing data //Journal of Physics: Conference Series. – IOP Publishing, 2014. – Т. 490. – №. 1. – С. 012113.

4. Ayman I. Statistical Research for Probabilistic Model of Distortions of Remote Sensing //Journal of Physics: Conference Series. – IOP Publishing, 2016. – Т. 738. – №. 1. – С. 012004.