Д.ф.-м.н., проф. А.В. Макаричев, А. А. Кудь, А. Б. Щукин

Национальный аэрокосмический университет «ХАИ»

Харьковский национальный автомобильно-дорожный университет

Московский государственный университет им. М.В. Ломоносова

СЛУЧАЙНЫЕ СУММЫ МИНИМУМОВ ПРИРАЩЕНИЙ ЗА ВРЕМЯ ОБСЛУЖИВАНИЯ В МНОКАНАЛЬНОЙ СИСТЕМЕ БЕЗ ОЖИДАНИЯ

В систему массового обслуживания поступает входящий поток требований с параметром , . В системе массового обслуживания требования обслуживаются без ожидания. Времена обслуживания требований неотрицательны и независимы в совокупности с функцией распределения . Предположим, что в начальный момент времени в системе массового обслуживания нет требований. За время обслуживания каждого требования с интенсивностью возникает случайное число независимых положительных случайных величин с функцией распределения , из которых находится условный минимум с функцией распределения и безусловный минимум с функцией распределения

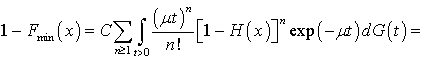
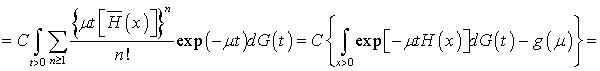
Здесь 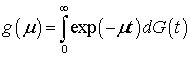- преобразование Лапласа времени обслуживания заявки, , а константа определилась из уравнения для равных значений правой и левой частей для значения . Итак, .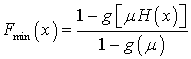

Предположим, что в момент времени в системе обслуживания нет

требований. Обозначим число требований, пришедших в систему

обслуживания на отрезке времени , - число обслуженных

требований в системе массового обслуживания на отрезке времени , а

- число требований, находящихся на обслуживании

в момент времени _. Очевидно

.

Распределение числа пришедших требований в систему на отрезке времени определяется по формуле [1]

,

где .

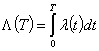Обозначим преобразование Лапласа для суммы

всех минимумов для всех требований, обслуженных на отрезке .

Обозначим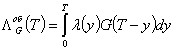

интеграл от интенсивности пуассоновского потока с переменным параметром

,

для числа поступивших на отрезке требований и обслуженных на нем.

Обозначим преобразование Лапласа для этого безусловного минимума. Тогда преобразование Лапласа для суммы

всех минимумов для всех требований, обслуженных на отрезке , имеет вид

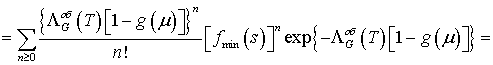
Дифференцированием ее в нуле находим математическое ожидание для суммы

всех сумм всех минимумов для требований, обслуженных на отрезке

,

второй момент этой случайной величины

,

и ее дисперсию

.

Здесь математическое ожидание минимума равно

.

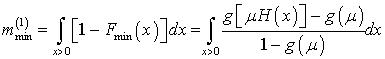А его второй момент можно вычислить по формуле

.

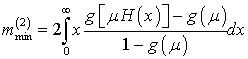Литература.

1. B. V. GNEDENKO AND I. N. KOVALENKO, Introduction to Queueing Theory, Program for Scientific Translations, Jerusalem, 1968.

2. Климов Г. П. Стохастические системы обслуживания, М., 1966, 244 стр. с илл.

3. Хинчин А. Я., Работы по математической теории массового обслуживания, Физматгиз, Москва, 1963, 236 стр.