Математика/ 3. Математичне моделювання

 

К.т.н. Шепетюк Б.Д., д.ф.-м.н. Нестерук І.Г.

Чернівецький національний університет імені Юрія Федьковича,  Чернівці, Інститут гідромеханіки НАН України, Київ, Україна

МОДЕЛЮВАННЯ ФОРМ СТІЙКИХ ВЕНТИЛЬОВАНИХ КАВЕРН

Для зменшення опору корпусів високошвидкісних підводних апаратів широко використовується  суперкавітаційний режим обтікання [1-2], що дозволяє значно знизити опір тертя через зменшення площі контакту з водою.  В роботах  [3-4] використовується спрощена модель одновимірного потоку ідеального нестисливого газу в кільцевому каналі між поверхнями тіла та каверни, що дозволяє отримати відповідне рівняння для радіуса R(x) тонкої осесиметричної стаціонарної вентильованої каверни. В роботі [5] одержано відповідне рівняння для радіуса R(x)  при наявності сили тяжіння:

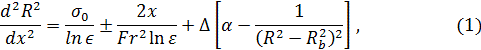
в якому всі довжини віднесені до радіуса каверни в точці її початку , а сталі параметри   та  визначаються формулами:

де  - число Фруда,  - прискорення сили тяжіння,  - густина газу, що використовується для піддуву (вважається сталою); V- його поточна швидкість;  Q- об’ємне витрачання газу; - швидкість, тиск газу та радіус каверни в перерізі початку  каверни х = 0;  - поточний та початковий радіуси тіла ( рис.1).

Fig2

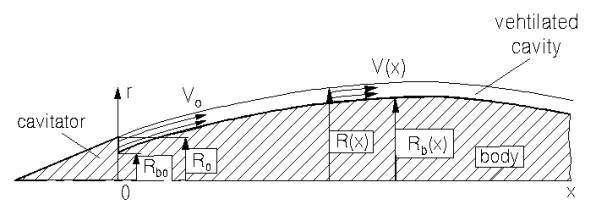
Рис. 1. Схема суперкавітаційного обтікання з інтенсивним піддувом

Стаціонарний випадок (1) справедливий при будь-яких значеннях швидкості вентиляції. Для того, щоб охарактеризувати вплив закачування газу, інші безрозмірні параметри можуть бути використані замість , наприклад,

                                  чи                         (5)

 де  - швидкість газу при . Безрозмірна швидкість вентиляції  - це відношення вершин тиску в газовому і водяному потоках при . Якщо силими тяжіння можна знехтувати також в потоці рідини (), то нелінійне диференціальне рівняння (1) збігається з отриманим в [3].

Використовуючи параметр  (9) можна переписати таким чином:

                                                                                 (6)

                                                                          (7)

                                                                                    (8)

         Стандартні початкові умови при

                                                                                                (9)

можуть бути використані для інтеграції (1) або (7), де  - похідна від радіуса тіла в порожнині. Як видно із (1) і (5), що вентиляція може сильно змінити форму суперкаверн тільки при малих значеннях  або при великому відношенні , так як   дуже мале.

Без вентиляції () рівняння (9) або (12) збігається із запропонованим в [6]. Розв’язок в цьому випадку може бути легко отриманий, використовуючи початкові умови (15):

                                                                   (10)

         Для вентильованих каверн необхідно вирішити нелінійне диференціальне рівняння (9) або (12). Видно, що уприскування газу сильно змінює форму порожнини не тільки при великих значеннях параметра , але і при дуже малих значеннях ширини каналу кругового .

Член в дужках (1)

                                                                              (11)

дорівнює нулю при  і може бути як позитивним, так і негативним при різних кавітаторах і формах корпусу. Це означає, що відповідна вентильована каверна може, відповідно, бути як більше, так і менше, ніж пара одного в (10). Приклади розрахунків можна знайти в [3] для першого випадку і в [4] для другого. Коли силами гравітації можна знехтувати, (1) або (6) показує, що два незалежних параметра, тобто тиск усередині каверни () і швидкість уприскування газу ( або , або ) впливають на форму каверни. Витік газу з стабільної штучної порожнини дорівнює швидкості подачі газу і залежить від розмірів порожнини, поведінки закривання порожнини, і так далі. Таким чином, витік газу також може бути різним при фіксованому кавітаційному числі (як рівне значенню швидкості подачі газу). Зокрема, це стверджується в [1], що «неможливо запропонувати  універсальний метод теоретичного визначення втрат газу». Цей висновок був підтверджений експериментами, де різні швидкості витоку/вприскування газу були отримані при фіксованому числі кавітації. Проте, є деякі спроби подати витік газу з пустого резонатора () при високих числах Фруда як функцію числа кавітації.

При використанні розроблених програмних   засобів моделювання впливу течій газу у вузькому каналі на форму тонкої (видовженої в напрямку руху) осесиметричної каверни [7] були одержані наступні кавітаційні криві (рис.2).

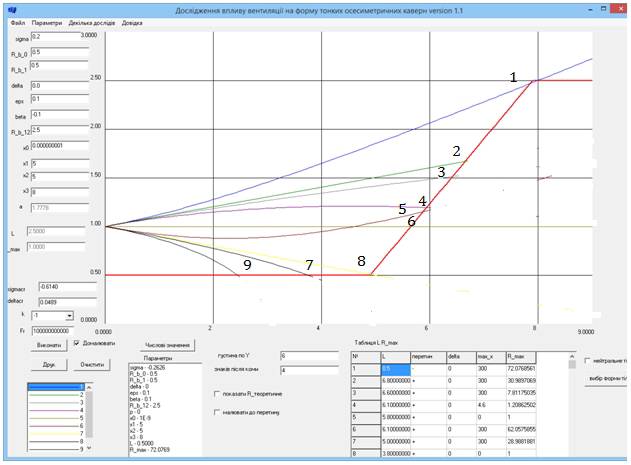
Image2-1.bmp

Рис. 2. Кавітаційні криві (конічно-циліндричний корпус,

На рис.2. представлені   кавітаційні форми для (10) при нульовій швидкості вентиляції на конічно-циліндричному корпусі (, , , , , )  для  (криві 14, значення числа кавітації  для і  (криві 6 - 9, значення і  0,2,  0,046, 0 і 0,2, відповідно).  Форми каверн,  що відповідають нульовому кавітаційному числу (криві 3, 5 і 8).

Слід зазначити, що серед каверн, представлених на рис 8 тільки криві 4 і 9 мають класичну еліптичну форму. Каверни 3 і 8 є параболічними, 2 і 7 мають конічну форму, 1 і 6 є гіперболічні, і 5 має циліндричну форму. Якщо x1 ,  то можна реалізувати тільки каверни 4, 7, 8 і 9. Інші каверни не можуть існувати в реальності без конічної частини корпусу (x1 ≤ x ≤ x2) відповідно до принципу стійкості, згаданого вище. Форми каверн, які відповідають нульовому кавітаційному числу (пунктирні криві 3, 5 і 8) не покривають корпус, як показано на рис.2.  Це означає, що при будь-якому значенні  і відсутності вентиляції всі три кавітатори (при   0 і - 0.1) не можуть створити каверну, досить велику, щоб покрити корпус.

 

Література:

1.        Логвинович Г.В. Гидродинамика течений со свободными границами К.Наук. думка.1969. -208с.

2.        Нестерук I. Г. Зменшення опору видовжених осесиметричних високошвидкiсних тiл.// Прикладна гiдромеханiка. 2009 Т. 11 (83), N 2. С. 55 – 67.

3.        Манова З.І., Нестерук І.Г., Шепетюк Б.Д. Оцінки впливу вентиляції на форму тонких осесиметричних каверн // Прикладна гідромеханіка. – 2011. Т.13 (85), № 2. – С. 44-50.

4.        Манова З.І., Нестерук І.Г., Шепетюк Б.Д.. Особливості форми донних штучних осесиметричних каверн// Прикладна гідромеханіка. – 2011. Т.13 (85), № 3. – с. 69-75.

5.        I. Nesteruk. “Shape of Slender Axisymettetric Ventilated Supercavites”, Journal of Computational Engineering, Volume 2014(2014), Article ID501590, 18 pages.

6.        I. Nesteruk, “On the shape of  a slender axisymettetric cavity iv a ponderable liquid”, Izvestija AN SSSR, Vol.6, pp.133-136, 1979.

7.        Шепетюк.Б.Д., Нестерук І.Г. Програмні засоби оцінки впливу вентиляції на форму тонких осесиметричних каверн. Matherifls of  the XI International scientific and practical conference, «Science and civilization-2015», 30 January- 07 Februare 2015. - Volume 23.  Mathematics. Modern information technologies. Sheffield. Science and education LTD, 2015. pp.12-19.