УДК 519.624.2.

Талайбеккызы Н., Баяндиев Е.Н., Махамбетжанов Д.Б.

Таразский государственный университет им. М.Х. Дулати, Тараз, Казахстан

Определить тип фазового портрета дифференциального уравнения первого порядка с помощью системы MAPLE.

Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную x, искомую функцию y=y(x) и ее первую производную y¢, т.е. уравнение вида

F(x,y,y¢)=0 или y¢=f(x,y).                                    (1)

Решением дифференциального уравнения называется функция y=j(x), такая, что при подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой этого уравнения.

Дадим теперь определение общего и частного решения дифференциального уравнения (1), правая часть которого удовлетворяет условиям теоремы Коши.

Функция y=j(x,c), зависящая от аргумента x и произвольной постоянной c, называется общим решением уравнения (1) в области Д, если она удовлетворяет условиям:

1) при любых значениях произвольной постоянной c, принадлежащих некоторому множеству, y=j(x,c) является решением уравнения (1);

2) какова бы ни была точка , лежащая внутри области D, существует единственное значение постоянной , такое, что решение y=j(x,c) удовлетворяет начальному условию .

Значение  можно найти из условия . Всякое

решение  уравнения (1), получающееся из общего решения y=j(x,c) при конкретных значениях , называется частным решением.

Начнем рассмотрение трех примеров обыкновенных дифференциальных уравнений (ОДУ) первого порядка:

Пример №1.

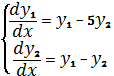
Решение этого примера в MAPLE имеет вид :

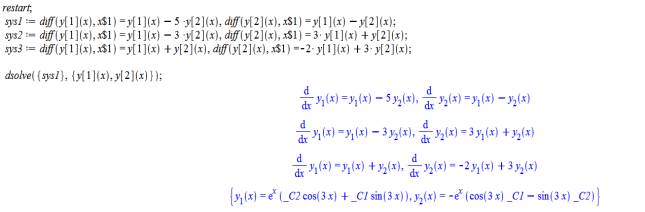
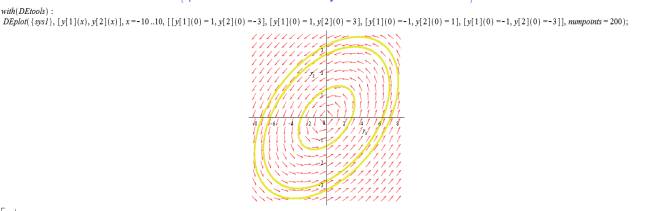
То есть, Тип собственных значений- чисто мнимые, тип особой точки –центр, тип фазовых траекторий- окружность , эллипс, вид фазовых траекторий- рис. 1.

Рис.1

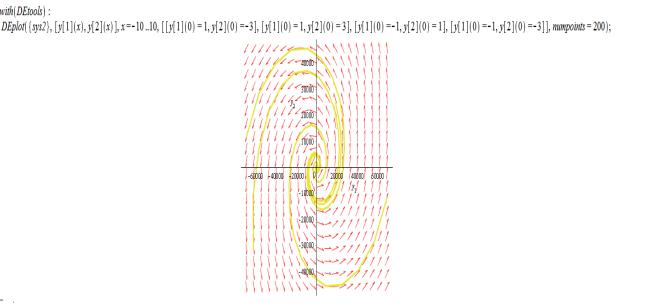
Пример №2.

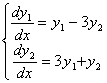
Решение этого примера в MAPLE имеет вид :

То есть, тип собственных значений-комплексные с положительной действительной частью, тип особой точки –неустойчивый фокус, тип фазовых траекторий- логарифмические спирали, вид фазовых траекторий- рис. 2.

Рис.2

Пример №3.

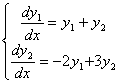
Решение этого примера в MAPLE имеет вид :

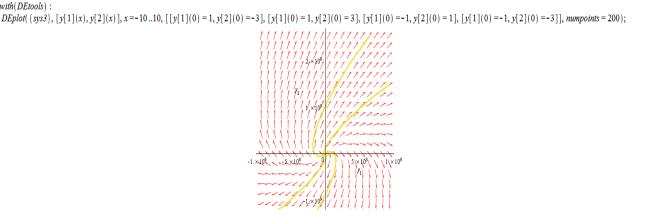
То есть, тип собственных значений- действительные положительные, тип особой точки –неустойчивый узел, тип фазовых траекторий- параболы, вид фазовых траекторий- рис. 3.

Рис.3

Литература:

1. Шалыгина Т.А. Белов Н.Н., Цепилевич Л.И. Дифферен- циальные уравнения. Учебное пособие. – Томск: Изд-во Том. гос. архит.-строит. ун-та, 2008. – 123 с.

2. Бугров Я.С. Дифференциальное уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Феникс, 1984-1997. – 512 с.