Кажикенова А.Ш., Алибиев
Д.Б., Турдыбекова К.М., Турдыбеков К.М., Герасимова К.
Карагандинский
государственный университет им. Е.А.Букетова,
г. Караганда, Казахстан
Итерационная схема
для решения сеточных уравнений
Навье - Стокса
Как известно, задача о стационарном движении
вязкой несжимаемой жидкости сводится к решению краевых задач [1]:
(uÑ)u
- Ñq =mDu+¦,
divu=0, (1)
![]() v =0.
v =0.
s
Кроме этого известно, что решение данной задачи
существует, и оно достаточно гладкое.
Рассмотрим следующую известную разностную
задачу [2]
![]() +
+![]() m=1,2 (2)
m=1,2 (2)
![]() (3)
(3)
![]()
![]() =0. (4)
=0. (4)
s1´s2
Оператор Lm,h является разностной аппроксимацией конвективных
слагаемых уравнений движения и имеет вид
Lm,h=![]() , (5)
, (5)
где ![]() такие, что
такие, что ![]() для всех сеточных
функций, определенных на W1´W2 с нулевыми значениями
на S1´S2. Например, в двумерном
случае можно записать в таком виде
для всех сеточных
функций, определенных на W1´W2 с нулевыми значениями
на S1´S2. Например, в двумерном
случае можно записать в таком виде
![]()
![]()
где
![]()
![]()
Теорема
1. Пусть ![]() . Тогда существует решение задачи (1)-(3) и для решения
справедлива оценка
. Тогда существует решение задачи (1)-(3) и для решения
справедлива оценка ![]() .
.
Доказательство. Будем использовать
лемму о неподвижных точках Брауэра.
Лемма
1. Пусть x®P(x)такое непрерывное
отображение Rm в себя, что для подходящего r>0, (P(x),x)³0, "x из сферы ½x½=r, где x=(xI),
z={zi}, мы полагаем, что (x,z)=![]()
![]()
![]() . Тогда найдется такое x, ½x½£r, что P(x)=0.
. Тогда найдется такое x, ½x½£r, что P(x)=0.
Умножим (1)
на um и просуммируем по
области W1´W2, и учитывая (5),
получим равенство ![]()
Отсюда следует, что ![]()
Составим вектор
x=![]() {u11/2,1,u11/21,…,u1N+1/2,1,…,u1-1/2N-1/2,…,uN+1/2,N-1/2, u1N+1/2,N+1/2,…,u21-1/2,…,u21,…,u2N+1/2,…,u2N-1/2,-1/2,…,u2N-1/2,N+1/2,u2N+1/2,-1/2,…,u2N+1/2,N+1/2,P11,…,P1N,…,PN1,…,PNN}.
{u11/2,1,u11/21,…,u1N+1/2,1,…,u1-1/2N-1/2,…,uN+1/2,N-1/2, u1N+1/2,N+1/2,…,u21-1/2,…,u21,…,u2N+1/2,…,u2N-1/2,-1/2,…,u2N-1/2,N+1/2,u2N+1/2,-1/2,…,u2N+1/2,N+1/2,P11,…,P1N,…,PN1,…,PNN}.
Положим, что вектор z=![]()
![]()
![]()
![]()
![]()
![]()
Тогда
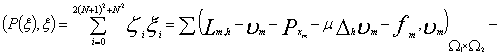
![]()
Значит ![]() если
если![]() , причем последние условия выполняются при
, причем последние условия выполняются при ![]() где
где![]() достаточно велика.
достаточно велика.
Отсюда в силу леммы
следует, что существует хотя бы одно решение задач (1)-(5). Покажем, что
решение задачи (1)-(3) устойчиво по правой части, если m - достаточное большое. В
самом деле, пусть ![]() и
и ![]() решение задачи (1)-(3),
соответствующее правой части f1,f2. Тогда для разностей получим
решение задачи (1)-(3),
соответствующее правой части f1,f2. Тогда для разностей получим
![]()
![]() (6)
(6)
![]()
![]()
![]()
![]()
![]() =
=![]() =0.
=0.
![]()
![]()
Преобразуем
нелинейные слагаемые
![]()
![]()
Умножим (6) на u1m-u2m,
просуммируем по области W1´W2 и в результате получим
![]() (7)
(7)
Оценим левую часть (7) по неравенству
Гёльдера
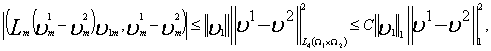
![]()
Отсюда из (7) следует, что ![]()
В свою очередь ![]() Отсюда следует, что
Отсюда следует, что ![]() при достаточно
большом m.
Итак, устойчивость разностных схем (1)-(3)
доказана.
при достаточно
большом m.
Итак, устойчивость разностных схем (1)-(3)
доказана.
Для нахождения решения (1)-(3) используется
итерационный процесс вида
![]() (8)
(8)
![]() (9)
(9)
![]() un+1 =0.
un+1 =0.
S1´S2
Список использованных источников
1.
Владимиров Н.Н., Кузнецов Б.Г., Яненко Н.Н. Численные расчёты симметричного
обтекания пластинки потоком вязкой несжимаемой жидкости. - В кн: Некоторые
вопросы вычислительной и прикладной математики. - Новосибирск, 1966. -с.29-35.
2.
Ладыженская О.А., Ривкинд В.Я. О сходящихся разностных схемах для уравнений Навье-Стокса
// Численный метод механики сплошной среды. - Новосибирск, ВЦ СО АН СССР, том
3. I97I. - № 1. - C.55-73.