Physics / 2 Solid State Physics

Prof. Urusova BI

Karachay-Cherkessia State University, Russia

The theoretical explanation of the magnetic viscosity of mining ores.

 It is known that the magnetic viscosity occurs at a slow change in the magnetization of a ferromagnet with time. Age of the Earth's crust is approximately years, this time is enough to provide a noticeable effect on the magnetization mining ores.

Now it is proved that the mining ores, there are two different types of magnetic aftereffect in ferromagnets - the viscosity due to the diffusion and viscosity due to thermal fluctuations, but unfortunately not enough reliable experimental data confirming the presence of a magnetic viscosity due to diffusion furnaces ores.

Therefore, we consider the appearance of the magnetic viscosity due to thermal fluctuations. Thermal fluctuations contribute to the movement of domain walls through the energy barrier, they can overcome the action of the weak geomagnetic field.

Neel, was supposed theory of viscosity of single-domain grains, in which the viscosity of the effect relates to the rotation process and then developed this theory for the case of solid ferromagnets. In this theory, the action of thermal fluctuations on shifts boundaries seen functioning field , additional to the current field - H. Then , can be expressed as:

, (1)

where Q - the constant of the order of 50; t- the duration of the field; - a constant that characterizes a sample that is independent of temperature and has the dimension of the magnetic field.

The intensity of magnetization after exposure can be expressed:

, (2)

where - magnetization in a field H, when the field is no viscosity; - irreversible differential susceptibility in point (hysteresis loop.

For the region Rayleigh instantaneous magnetization is:

, (3)

And irreversible susceptibility at ( is 2ВН, then the expression (2) can be rewritten as:

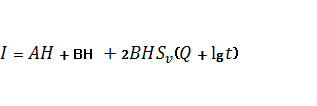(4)

 After removing the residual magnetization field H is equal to ½ and the irreversible susceptibility - BH, so residual magnetization at the time after the field is:

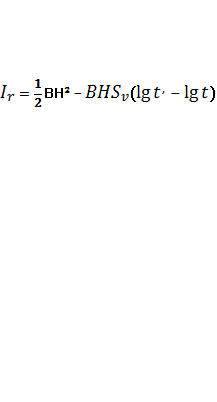, (5)

where time t- field action H.

Neel theoretical calculation for the critical variable magnetic field - , necessary for the destruction of residual magnetization gives the following relationship:

, (6)

where H - the applied field; t - time of relaxation.

Theoretically calculate by Neel model is:

, (7)

where k is the Boltzmann constant; T - the absolute temperature; v- volume of the region corresponding to the Barkhausen jumps.

If we consider the impact of fluctuations in the height of the potential barrier, is:

(8)

where - spontaneous magnetization; v- volume of the magnetization reversal region corresponding to the Barkhausen jump; α- constant less than one, depending on the orientation of the boundary with respect to the magnetic field.

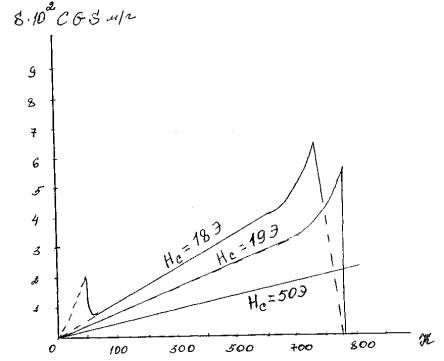Comparing the expression (8) and (7) we see that the temperature dependence of expressed by - differently. If v is independent of temperature, in (7) changes in proportion to by the formula (7), but proportional to T according to the formula (8) (see Figure 1).

Figure 1. Temperature dependence of the magnetic viscosity coefficient S.

From Fig. 1 that the coefficient of viscosity with temperature, in the region of 200⁰К<Т<400⁰К viscosity caused no internal field variance and fluctuation in the height of the potential barrier.

Fig. 2 shows the change in viscosity - S depending on the magnetic field.

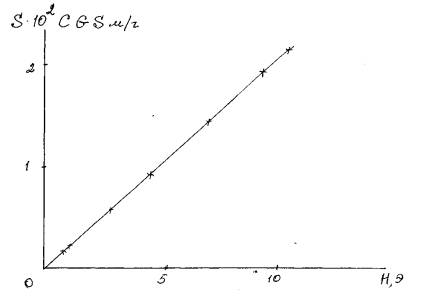
Figure 2. Changes in the magnetic viscosity coefficient S according

the magnitude of the applied magnetic field.

From Fig. 2 shows that the magnetic viscosity coefficient for Rayleigh field region is a linear function of the applied magnetic field and temperature than close to the Curie temperature.