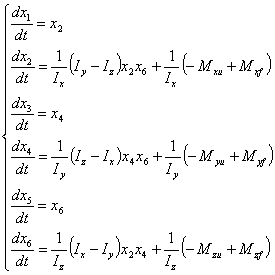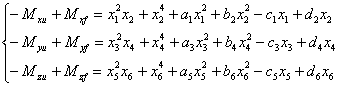ТЕХНИЧЕСКИЕ НАУКИ/12.Автоматизированные системы управления на производстве.

Д.т.н., профессор Бейсенби М.А., докторант PhD Закарина А.Ж., докторант PhD Булатбаева Ю.Ф.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Система управления с повышенным потенциалом робастной устойчивости нелинейным КЛА в классе параболическая омбилика

В данной работе рассматривается космический летательный аппарат (КЛА) как твердое тело, которое под воздействием приложенных к нему сил совершает вращательно-поступательное движение, а именно центр масс КЛА перемещается по неподвижной в инерциальном пространстве траектории и одновременно с этим совершает вращательные движения относительно центра масс КЛА. Движение центра масс при исследовании вопросов ориентации и стабилизации не учитываем, так как траектория считается заданной. Управление вращательным движением КЛА осуществляется с помощью системы ориентации и стабилизации.

Целью управления является стабилизация желаемого состояния. Эта цель соответствует устойчивости системы управления движением КЛА при любых изменениях неопределенных параметров, то есть таких параметров как угол тангажа, угол рыскания и угол крена.

Рассмотрим нелинейную систему управления КЛА [1]:

(1)

где , , , и , , углы тангажа, рыскания и крена соответственно.

Закон управления возьмем в виде четырех параметрических структурно-устойчивых отображений:

(2)

где ,,- главные центральные моменты инерции КА относительно соответствующих осей ,, и ,, соответственно проекции управляющего и возмущающего моментов на соответствующие оси. При синтезе алгоритма используем функции Ляпунова [2].

Вычисляя алгебраические уравнения, находим, что стационарными состояниями системы являются ненулевые решения уравнений:

₍₃₎

Другими стационарными состояниями системы (1) являются:

, , , , , , (4)

Для определения области устойчивости стационарного состояния (3) находим компоненты вектора градиента и разложение компонентов вектора скорости по координатам. Таким образом, находим полную производную по времени от вектора-функции Ляпунова:

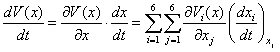(5)

Функция (5) является знакоотрицательной функцией, и достаточное условие асимптотической устойчивости гарантировано будет выполняться.

По компонентам вектора градиента построим компонента вектор-функций Ляпунова и представим в скалярной форме:

(6)

По теореме Морса [3] сложную функцию (6) можем заменить эквивалентной ей квадратной формой. Опуская сложные вычисления, получим:

, (7)

Условие существования положительно определенной функции будет выражаться неравенствами:

, , , , , , (8)

Из выше приведенных рассчетов, можно сделать вывод, что стационарное состояние (3) системы (1) являются устойчивым при изменении параметров КЛА в области (8), а стационарное состояние (4) появляется при потере устойчивости состояния (3) и они одновременно не существуют. Стационарные состояния КЛА (3) и (4) являются устойчивым при выполнении системы неравенств (9):

, , , , , , , , . (9)

Литература:

1. Попов В.И. Системы ориентации и стабилизации космических аппаратов. – М.: Машиностроение, 1986. – 183 с.

2. Барбашин Е.А. Функции Ляпунова. – М.: Наука, 1976. – 240 с.

3. Beisenbi M., Abitova G., Nikulin V., Skormin V., Ainagulova A. Control System with High Robust Stability Characteristics Based on Catastroph Function. 17^th IEEE. Paris, France, 2012. – P. 273-279.