Д.т.н. проф. Кохреидзе Г.К., докторант Прангишвили Гр.В., бакалавр Тетунашвили Е.Р.

Грузинский технический университет, Грузия.

Компьютерное моделирование электромагнитных переходных процессов в встречно-параллельно соединенных выпрямительно-инверторных агрегатах.

Силовая схема выполнена в виде двух встречно-параллельно включенных трехфазных тиристорных мостов выпрямительного и инверторного агрегата. Оба моста постоянно подключены к ответвлениям вентильных обмоток преобразовательного тягового трансформатора.

Для компьютерного моделирования электромагнитных переходных процессов используем комплексное преобразование переменных.

Введены результирующие комплексные величины: 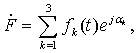-число фаз, -углы, определяемые магнитными осями фаз.

Для обратного перехода от комплексных величин к действительным фазным значениям необходимо вводит сопряженные столбцовые матрицы[1,2,3]

В результате комплексного преобразования переменных получаем скалярные уравнения относительно составляющих результирующих величин и токов выпрямителя и инвертора :

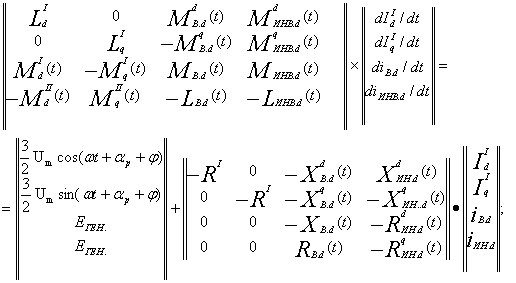(1)
В (1) все переменные индуктивности и сопротивления выражены через заданных параметров всей цепи.

Полученное матричное уравнение(1) является основой для компьютерного моделирования электромагнитных переходных процессов в соответствующих агрегатах.

В результате решения уравнения (1),некоторого преобразования и введения соответствующих обозначении, получаем выражения производных токов, дающий возможность провести компьютерное моделирование электромагнитных переходных процессов.

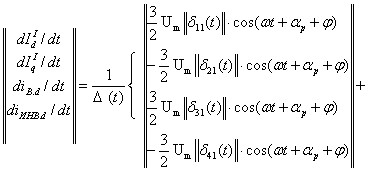
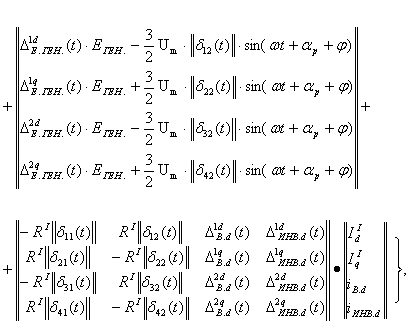(2)

где в (2) для определителя имеем:

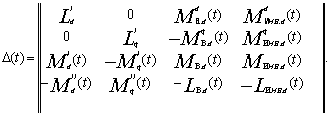₍₃₎

В (2) переменные параметры - представляет минор элемента . Остальные переменные эквивалентные коэффициенты выражаются через заданных параметров единых преобразовательных систем.

Интегрируя матричные уравнения (2) от до времени, получим интегральные выражения составляющих токов в обобщенном виде:

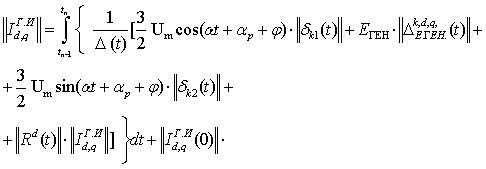₍₄₎

На основании выражения (4) можно построить структурную схему модели переходных процессов всех токов системы как во в не коммутационных, так и в коммутационных интервалах времени.

На схеме в не коммутационный интервал регулируется ключом , а коммутационный интервал ключом

В выражений (4) соответственно имеем :

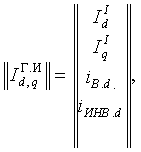
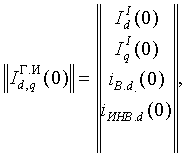(5)

Список литературы

1. Л. О. Чуа; Пен-Мин Лин. Машинний анализ электронных схем (алгоритмы и вычислительные методы). Перевод с английского. Москва «Энергия» 1980. 638 с.

2. С.Г. Герман-Галкин. Компьютерное моделирование полупроводниковых систем. МАТLAB 6.0 Корона принт, 2001. 320с.

			Um	G
t

∑

1

X

1

t_n-1

1

∑

1

1

G

ω

t_n

K₁

K

1

1

1

1

X

1

1

X

1

G

U_m

sin

1

1

X

1

1

G

ϕ

α_P

V k₂

K

E

1

1

1

Рис.1 Структурная схема

модели переходных процессов матриц токов преобразовательной системы в унифицированной форме.