Математика /4.Прикладная математика
К.п.н. Токмазов Г.В.
Государственный морской университет имени
адмирала Ф.Ф.Ушакова ,
Россия
Исследовательские задачи динамической
прикладной математики морского флота
Исследовательские задачи динамической
прикладной математики морского флота отражают математическое моделирование
основных элементов транспортных объектов. При этом формируется профессиональное
мышление, отражающее единство деятельностных и предметных условий в процессе реализации
исследовательских проблем прикладной математики морского флота. Рассматриваются: динамика груза и закон его движения в трубе
перевалочного морского погрузчика; динамика и закон движения призматической
тележки палубного морского механизма; динамика и
закон движения шара-датчика автоматизированной системы судового управления;
динамика и закон движения судовой транспортной механической системы на морском флоте.
В процессе решения исследовательских
задач динамической прикладной математики морского флота необходимо применять
основные положения теории деятельности, исследовательского анализа и теории
формирования профессионального мышления.
Исследовательский анализ предполагает
выполнение последовательности познавательных аналитических действий: определить
условия анализа – задачу динамической прикладной математики морского флота (ЗДПММФ)
как целое; проанализировать условия возникновения ЗДПММФ; установить функциональную
сложность ЗДПММФ; определить внешние, материальные параметры ЗДПММФ относительно
пространственных, временных, силовых, энергетических и гравитационных
характеристик; проанализировать строение функций ЗДПММФ; установить функциональные
элементы сложности анализа ЗДПММФ; определить внутренние свойства и динамику ЗДПММФ.
Задача 1
На вертикальном участке АВ трубы перевалочного
морского погрузчика на груз D массой m = 8 кг
действуют сила тяжести и сила сопротивления 
; где 
, движение от
точки A, где vo = 0, до точки В
длится t1 = 2 с. На наклонном участке ВС перевалочного морского
погрузчика на груз действуют сила трения (коэффициент трения груза о трубу
равен f = 0,2) и переменная сила F=r(t) 
,
заданная в Hьютонах 
. Определить x = f(t) - закон движения груза на участке ВС перевалочного морского
погрузчика.
Ответ:
где х
- в метрах, t - в секундах.
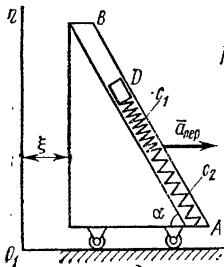
Задача 1
Задача 2
Задача 2
Груз D массой m = 0,4 кг,
прикрепленный к двум последовательно соединенным пружинам с коэффициентами
жесткости c1 = 200 Н/м и с2 = 50 Н/м, перемещается
по пазу АВ призматической тележки палубного морского механизма. Тележка движется по закону 
и 
. Начальное удлинение пружины с эквивалентной
жесткостью 
=0,1 м ,
а начальная скорость груза по отношению к тележке палубного морского механизма vo=1м/с
направлена от В к D и 
. Определить: х =
f(t) - закон движения груза по
отношению к тележке палубного морского механизма.
Ответ:
где х - в метрах, t
- в секундах.
Задача 3
Датчик автоматизированной системы судового управления
в виде шара весом Р нанизан на
расположенный в вертикальной плоскости гладкий направляющий управляющий стержень,
изогнутый так, что часть BD его является дугой окружности радиуса
R
= 0,6 м . К шару-датчику прикреплена пружина с коэффициентом жесткости 
; длина недеформированной пружины равна ℓo =1,5R. Движение шара-датчика начинается из точки Во,
находящейся на высоте Н = 2R; в точке В шар-датчик освобождается от
пружины и движется дальше по дуге BD, 
, OC =0,75R. Определить: 1) скорость шара-датчика в точке B1;
2) Q1— силу на стержень в
давления шара-датчика точке B1.
Ответ: v = 5,36 м/с; Q1 = 5,38 Р.
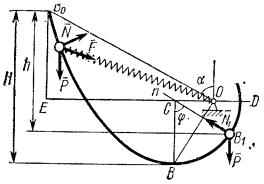
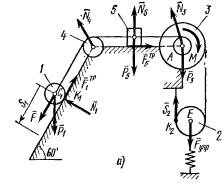
Задача 3 Задача 4
Задача 4
Cудовая транспортная механическая система состоит из сплошного
однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с
радиусами ступеней R3 и r3
и радиусом инерции относительно оси вращения ρз, блока
4 и груза 5 (коэффициент трения груза о плоскость равен f ). Тела системы
соединены тросами, уложеными на шкив 3. К центру Е блока 2 прикреплена
пружина с коэффициентом жесткости с; ее начальная деформация равна
нулю. Система приходит в движение из состояния покоя под действием силы F=f(s),
зависящей от перемещения s точки ее приложения. На шкив 3
при движении действует постоянный момент М сил сопротивления. Определить 
в тот момент
времени, когда 
.
Ответ:
.