Технические науки / 6.Электротехника и радиоэлектроника.

к.т.н. Черных А.Г., аспирант Бузунов А.С.

Иркутский государственный аграрный университет, Россия

ПРИМЕНЕНИЕ МЕТОДА СИММЕТРИЧНЫХ

СОСТАВЛЯЮЩИХ ДЛЯ РАСЧЕТА НЕСИММЕТРИЧНЫХ РЕЖИМОВ РАБОТЫ ТРЕХФАЗНЫХ СЕТЕЙ

Проведение расчетов несимметричных режимов описывающих токораспределение  в трехфазных электрических сетях в фазных координатах, как правило, связано с трудоемкими матричными операциями при решении системы линейных алгебраических уравнений высокого порядка, для решения которой могут использоваться прямые методы, такие, как модификация метода Гаусса, методы окаймления и др.

Например, связь между вектором падения напряжения вдоль участка линии   и вектором токов в фазах  будет иметь вид следующего матричного равенства:

Соответственно, уравнения по определению емкостных токов в фазах  через частичные емкостные проводимости фаз линии  можно представить в виде

Существенного упрощения при решении данных уравнений можно добиться введением матричного преобразования подобия , позволяющего диагонализировать матрицу погонных параметров  и матрицу частичных емкостных проводимостей . Наибольшее распространение получило преобразование фазных координат к симметричным составляющим – прямой, обратной и нулевой последовательностям (система координат 1–2–0).

Для определения коэффициентов матрицы , один из столбцов матрицы выберем таким образом, чтобы в наиболее часто встречающемся симметричном режиме, когда напряжения и токи фаз образуют систему прямой последовательности где , какое-либо из фазных напряжений (или токов), например, определялось только одной сосотавляющей – . Аналитически указанное ограничение можно записать следующим образом: . Тогда

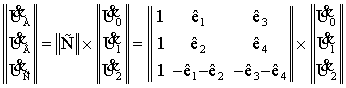
или

Если выбрать такие значения коэффициентов, что будут выполняться следующие тождества , то значения фазных напряжений будут определяются только одной составляющей – .

В свою очередь, сделанное допущение о том, что при симметричном режиме, когда напряжения и токи фаз образуют систему обратной последовательности , значения фазных напряжений определяются только  одной составляющей –, позволяет получить дополнительные ограничения в виде . При этом значения коэффициентов удовлетворяют соотношениям:  .

Матрица преобразований  (преобразование а-в-с ® 1-2-0), удовлет-воряющая первому и второму допущению имеет вид:

 

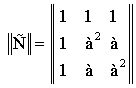                                                                                                       (1)

Пусть трехфазный несимметричный потребитель  с сопротивлениями   и   питается от источника электрической энергии (э.д.с.   и )  по схеме четырехпроводного соединения «звезда» через линию передачи (рис. 1). Провода линии передачи с сопротивлениями   и  соединены последовательно с соответствующими фазами приемника, а нейтральные точки источника (·) N и приемника (·) n соединены через комплексное сопротивление  (рис. 1).

 

 

 

 

 

 

 

 

 

 

Пусть и – комплексные сопротивления соответствующих фаз источника;      и  – комплексы сопротивлений взаимоиндуктивности фаз источника, соответствующих индексам.

С учетом введенных обозначений уравнения электрического равновесия по второму закону Кирхгофа для независимых контуров включающих соответствующие фазы приемника (рис. 1) запишутся в виде

                                                                           (2)

                                  

                                                                  (3)

                                 

Введем следующие допущения и соответствующие им обозначения

 

                   

С учетом введенных обозначений для системы уравнений (2) и (3) имеем

                                           (4)

                                           (5)

                                           (6)

Для узла n на основании первого закона Кирхгофа имеем

                                                         (7)

Учитывая, что  а  найдем сумму уравнений (4) ¸ (6), получим

или

                                             (8)

где

                                                                                     (9)

– сопротивление нулевой последовательности.

При выполнении последующих преобразований, с учетом формулы Эйлера для единичного вектора оператора воспользуемся соотношениями:

                                     (10)

                              (11)

                                         (12)

                    (13)

                (14)

                                         (15)

                                     (16)

                               (17)

                                     (18)

                  (19)

               (20)

Умножим уравнение (5) на оператор а уравнение (6) на оператор  и сложим с уравнение (4). После упрощений полученного тождества с учетом выражений (10) ¸ (15), окончательно имеем

или

                                              (21)

где

                                             (22)

– сопротивление прямой последовательности.

Умножим уравнение (5) на оператор а уравнение (6) на оператор  и сложим с уравнение (4). После упрощений полученного тождества с учетом выражений (10) ¸ (20), окончательно имеем

или

                                          (23)

где

                                         (24)

– сопротивление прямой последовательности.

Воспользуемся уравнениями (9),   (22)  и  (24) и установим соответствие между коэффициентами линейных преобразованийи , , .

Найдем сумму уравнений (9), (22) и (24)

или

                                  (25)

Умножим уравнение (22) на оператор  а уравнение (24) на оператор  и сложим с уравнение (9)

или

                               (26)

Умножим уравнение (22) на оператор  а уравнение (24) на оператор  и сложим с уравнение (9)

или

                              (27)

Уравнения (8), (9) и (21) ¸ (24) устанавливают однозначную связь между электрическими величинами и электрическими параметрами при переходе от фазных координат к симметричным составляющим – прямой, обратной и нулевой последовательностям (система координат 1–2–0).

Следует отметить, что три уравнения (8), (21) и (24) содержат шесть неизвестных величин: три составляющих напряжения ( ,,) и три составляющих тока (,,). Недостающие уравнения для определения неизвестных величин получают из граничных условий, которыми характеризуется тот или иной вид не симметрии.

Если в качестве источника электрической энергии (рис. 1) используется трансформатор , то уравнения (9), (22) и (24) примут вид

откуда следует, что

Для частного случая, когда между элементами трёхфазной цепи нет индуктивной связи, имеем

При симметричном потребители, например, асинхронном двигателе обмотки которого соединены звездой с заземленной нейтралью, для принятых на рис. 1 обозначений, уравнения электрического равновесия по второму закону Кирхгофа для независимых контуров включающих соответствующие фазы двигателя определятся выражениями

                                  (28)

                                 (29)

                                 (30)

где,                 

Можно показать, что после преобразований  урав­нений (28) ¸ (30), аналогичных преобразованиям, проведенным для уравнений  (4) ¸ (6), связь между симметричными составляющими в системе координат 1–2–0 имеет вид:

  

 Литература:

1. Касаткин А.С. Курс электротехники: Учеб. для вузов. – 9-е изд., стер. – М.: Высш. шк., 2007. – 542 с.

2. Черных А.Г. Несимметричный режим однофазного замыкания при нейтрали сети, заземленной через дугогасящий реактор. / А.Г. Черных, А.М. Сыроватский // Материали за 11-а международна научна практична конференция, «Найновите постижения на европейската наука», 17 – 25-ти юни, 2015. Том 13. Технологии. Селско стопанство. Здание и архитектура. София. «Бял ГРАД-БГ» – pp. 32 - 41.