Создание алгоритма ускоренного определения
коэффициента теплопередачи кузова изотермического транспортного средства
А.А. Голубин1, С.Н. Науменко2
1 Общество с ограниченной ответственностью «Центр безопасности информации»
(ООО «ЦБИ»), Королев, 141090, Россия
2
Акционерное
общество «Научно-исследовательский институт железнодорожного транспорта (АО
«ВНИИЖТ»), Москва, 129626, Россия
ВВЕДЕНИЕ
Необходимость экономии
топливно-энергетических ресурсов ежегодно увеличивает спрос на
высокоэффективные строительные материалы и конструкции, позволяющие обеспечить
более высокое сопротивление теплопередаче и, соответственно, сократить затраты
на отопление или кондиционирование воздуха в помещениях. Применительно к
изотермическим транспортным средствам (ИТС), основной нормативной величиной,
характеризующей теплотехнические свойства ограждающих конструкций кузовов ИТС,
является значение коэффициента теплопередачи – К (Вт/м2 К). [1] Сложившаяся в мировой практике
процедура по определению К, несмотря
на высокую точность выполняемых измерений с относительной погрешностью не более
5%, тем не менее остается длительной и связана со значительными простоями ИТС в
специальной теплоизолированной испытательной станции. Поэтому
минимизация продолжительности процедуры проведения испытаний ИТС по определению
К является достаточно актуальной.
РЕШЕНИЕ
Предлагаемый алгоритм определения К позволяет определить его с относительной погрешностью не более
5%, и, при этом, значительно сократить время проведения испытаний.
Так, известно дифференциальное уравнение теплового баланса нагреваемых тел:
[2]
(1)
где: W – водяной эквивалент тела;
Р – мощность нагревателя
тела;
К – коэффициент теплопередачи
тела;
Н – геометрическая (среднегеометрическая) поверхность тела;
– перепад температур
внутри и снаружи тела;
– текущее время.
Преобразуем его в виде: 
(2)
где: V1 – скорость
изменения перепада температур тела.
При V1 = 0 обеспечивается равновесный режим.
Обозначим в (2):
;
Тогда выражение запишется как:
(3)
Таким образом, получаем, что V1 линейно зависит
от .
Ранее [3] было замечено, что с момента включения нагревателя и до момента,
когда выполняются условия уравнения (2), проходит некоторое время, в течение
которого перепад температур изменяется в
соответствии с уравнением:
(4)
где: – текущее время от
момента включения нагревателя;
А и В –
параметры уравнения.
Тогда, из (4) находим: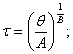 
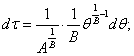
(5)
где: V2 – скорость изменения перепада температур тела на начальном участке после
включения нагревателя.
Таким образом, с момента включения нагревателя до момента, при котором
выполняются условия уравнения (1), изменение скорости V2 происходит по кривой, описываемой степенной функцией уравнения (5). В
момент, когда начинают выполняться условия уравнения (1) скорость V1 начинает изменяться по
прямой, описываемой уравнением (3). В этот момент происходит касание
криволинейной степенной функции уравнения (5) и прямолинейной функции уравнения
(3). При этом V2 = V1 и далее V1 изменяется прямолинейно в соответствии
с уравнением (3).
Обозначим параметры V, и точки касания
соответственно через Vк, к и к.
Тогда:
(6)
При известных параметрах точки касания можно уравнение касательной прямой
выразить через параметры касаемого криволинейного уравнения, исходя из
равенства:
(7)
где:
V2 и – текущие значения
параметров;
и к – известные значения параметров в точке касания.
Отсюда:
8)
Дальнейшие преобразования с учетом (3-5) позволяют получить выражение для К:
(9)
Следует, однако, иметь в виду, что во время включения нагревательных
элементов, начальная разность температур может не равняться нулю, а быть
несколько больше нуля. В этом случае выражения (4) и (9) запишутся
соответственно в виде:
(10)
(11)
где: 
– время,
соответствующее начальному значению разности температур о на
момент включения нагревательных элементов: 
Из выражения (11) видно, что значение К
зависит от параметра В, который
входит как в числитель, так и в знаменатель.
Известно [4], что при нагреве функция (4) является выпуклой. Это возможно
только при значениях В<1, т.к. при
значениях В=1 функция превращается в
линейную типа 
а при значениях В>1 - в вогнутую функцию.
Таким образом, параметр В
изменяется в пределах от 0 до 1.
При В=0 значение разности
температур 
перестает зависеть от времени 
. Это значит, что перепад температур остается постоянным во
времени и значит процесс нагрева не происходит.
Исследование зависимости параметра Р:А
в уравнении (11) от параметра В показало его линейную зависимость типа:
Р : А=1,237В (12)
Обозначим
Р : 1,237В = Аα, (13)
а значения , соответствующее значению Аα, через 
и предположим, что
среднее за эксперимент значение перепада температур 
должно оставаться неизменным,
как при значениях , так и при значениях :
(14)
где: 
- время окончания
эксперимента.
отсюда:
(15)
К
может меняться в пределах от нуля, тогда теплообмен тела с окружающей средой
отсутствует, до 1, когда вся мощность
нагревательных элементов беспрепятственно уходит в окружающую среду через
ограждающуюся поверхность тела. Сравнение параметров В и К показывает, что при
В=1, когда разность температур
остается неизменной, коэффициент К
равен 1, т.к. вся мощность
нагревателей уходит в окружающую среду. Вместе с тем, при В=1 перепад температур прямо пропорционален времени нагрева. Это
возможно только при отсутствии теплообмена с окружающей средой, когда
коэффициент К=0.
Отсюда следует, что коэффициент К
и параметр В взаимопротивоположны,
т.е.:
К = 1 – В (16)
Как видно из выражения (11), в его правую часть входят комплексы (1-В), Р:А и 1:
.
Ранее, (12) было показано, что комплекс Р
: А =1,237 В. Очевидно, что для равенства К и (1-В) в выражении (11),
произведение комплекса Р:А и
комплекса 1: должно быть всегда равно 1.
Отсюда:
1:1,237
В=1: (17)
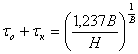(18)
Таким образом, для определения коэффициента К необходимо определить параметр В и затем вычислить его по выражению (16).
ВЫВОДЫ
1.
Представленный
алгоритм опытного определения коэффициента теплопередачи изотермического
транспортного средства дает возможность сокращения длительности проведения
испытаний в 6-9 раз.
2.
Ускоренный способ
проведения испытаний по определению К
позволяет увеличить производительность испытательных станций, допуская переход
от практикуемого в настоящее время выборочного контроля изготавливаемых или
ремонтируемых изотермических транспортных средств к их повсеместному контролю.
3.
Применение
экспресс-метода по определению К открывает возможности для эксплуатирующих
компаний к организации электронного паспорта теплотехнического состояния для
каждого кузова изотермического транспортного средства, контроль над которым
решает задачу обеспечения энергооптимальных режимов работы энергетического
оборудования, а следовательно и увеличения его ресурса.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Ибраев К.А., Дынга И. Г., Кондратьев А.В. Контроль и
освидетельствование изотермических транспортных средств // Автотранспортное
предприятие. 2006. № 9. С. 20 – 24.
2. Михеев М.А., Михеева И.М. Основы теплопередачи.
Москва, "Энергия" 1977
г. 343с.
3. Способ определения среднего коэффициента теплопередачи
кузова транспортного средства: а.с. № 1730572 СССР /И. П. Екимовский, А.В.
Коковихин, Н.С. Теймуразов и др. Опубл. 30.04.1992. Бюл. № 16. 11 с.;
4. Бартош Е. Т. Энергетика изотермического подвижного состава. М.: Транспорт, 1976. 304 с.