MEL’NICK V.M.
NATIONAL TECHNICAL
UNIVERSITY OF UKRAINE "IGOR SIKORSKY KYIV POLYTECHNIC INSTITUTE"
MANIFESTATION OF THE SELECTIVITY EFFECT OF THE QUANTUM
OF KINEMATIC AND ACOUSTIC DISTURBANCES
An integrating gyroscope is intended for
measuring the turning angle of the aircraft in relation
to the measuring
(ingoing) axis of the device. Unlike the angle rate sensor, it does not contain a spring,
and the functions
of damper are performed by a liquid-and-static constituent of the
gimbal.
The equations of the first
and second approximations
can be obtained from the corresponding equations of ÄÓÑÓ, if we can take up in them -
In
other words
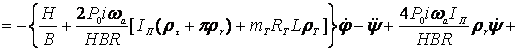
(1)
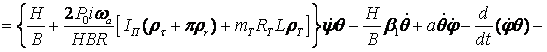
(2)
The solution of these equations
for the synchronous and
asynchronous
harmonic oscillations of the aircraft can
be obtained from the
previously obtained results. For the synchronous oscillations of the fuselage - are expressions and, for the
asynchronous oscillations of the
aircraft - are expressions and :
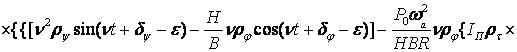
(3)
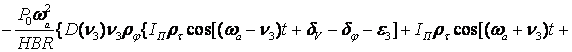
(4)
where 
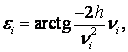
1,2,3.
The second approximation is written down analogically for the synchronous
and asynchronous tossing.
From the given correlations it is following, that at the
compatible action of kinematics and
acoustic inciting on the device , even in the first
approximation
it is possible
to find out
the systematic drift of the initial signal of the gyroscope. It takes
place at the
equality of frequencies of kinematic and
acoustic inciting, in
other words at the implementation of condition 
. Systematic drift of
the axis of the
device takes place both at
synchronous
and asynchronous tossing of the aircraft fuselage [1, 2].
The stable constituents in
the right part of the expressions (3) and (4)
are of great practical interest. The stable value of the initial signal of the device will equal
; 
We will find out the
stable constituent C. Averaging in time will
be denoted by
the symbol
. Then in
the right part of the expression (4)
we will distinguish the
stable values, in other
words we will carry out the following
procedure -
As a result we have for synchronous
oscillations -
(5)
Analogical for asynchronous oscillations -
(6)