Математика/ 1. Диференціальні і інтегральні рівняння

К.ф.-м.н.  Казмерчук А.І.

Прикарпатський національний університет імені В.Стефаника

Розпад розриву в системах законів збереження з порушенням умови гіперболічності.

Розглянемо задачу Рімана для системи квазілінійних рівнянь першого порядку   

(1)

(2)

Тут . Відомо ([1]), що для окремих задач для гіперболічної сильно нелінійної системи стійкий розв’язок існує і містить не більше хвиль. В даній роботі пропонується підхід отримання стійких розв’язків для систем з порушенням як умови гіперболічності, так і умови сильної не- лінійності. При цьому розв’язок задачі (1), (2) матиме в загальному випадку навіть зліченну кількість хвиль, серед яких зліченна кількість центрованих хвиль розрідження і зліченна кількість ударних хвиль

ТЕОРЕМА 1 Нехай матриця складається з блоків. А саме, для набору натуральних чисел таких, що , лише при . Нехай кожна з матриць гіперболічна, і для неї існує стійкий розв’язок відповідної задачі Рімана. Тоді вектор-функція є стійким розв’язком задачі Рімана (1),(2).

Тут під стійким розв’язком ми розуміємо такий, який задовольняє ентропійну умову ([2]) для узагальнених розв’язків задачі Коші для рівняння (1). Наступний приклад ілюструє метод побудови стійкого розв’язку задачі (1),(2). Нехай .

(3)

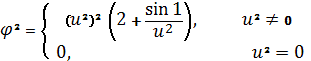(4)

a) . У цьому випадку розв’язок містить одну хвилю, що складається з двох ударних хвиль компонент.

b) . У цьому випадку розв’язок містить одну хвилю, що містить центровану хвилю першої компоненти і ударну хвилю другої компоненти.

c) . У цьому випадку розв’язок містить зліченну кількість хвиль, що містять почергово або центровану хвилю розрідження або ударну хвилю другої компоненти. При цьому ці хвилі накопичуються і мають граничне положення , де крім того розташована ударна хвиля першої компоненти.

d) . У цьому випадку розв’язок містить зліченну кількість хвиль, що містять почергово або центровану хвилю розрідження або ударну хвилю другої компоненти. При цьому ці хвилі накопичуються і мають граничне положення , в околі якого розташована центрована хвиля розрідження.

Література:

1. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой динамике. - М., Наука,1978.

2. Lax P.D. Hyperbolic system of conservation laws.-Comm. Pure Appl.Math.-1957.-V.10.-p.537-566.