Хомченко А.Н.
Черноморский
государственный университет им. Петра Могилы, Николаев, Украина
ОСОБЕННОСТИ
ПОЛИНОМИАЛЬНОГО ИНТЕРПОЛИРОВАНИЯ ФУНКЦИЙ ДВУХ АРГУМЕНТОВ.
Введение. Интерполирование
функций нескольких аргументов принципиально отличается от интерполирования
функций одного аргумента наличием специфических трудностей [1]. Появление и
развитие метода конечных элементов (МКЭ) стимулировали во второй половине ХХ
века новую волну повышенного внимания к задачам восстановления функций многих
аргументов [2,3]. Появились новые интересные задачи полиномиального
интерполирования на конечных носителях. Особый интерес представляют
оригинальные и неожиданные результаты, не имеющие аналогов в теории функций
одного аргумента. Прежде всего это касается элементов серендипова семейства. Ниже
пойдет речь об элементе Q12, который реализует
бикубическую интерполяцию на квадрате (quadrilateral) с 12 узлами.
Главная
особенность серендиповых элементов высших порядков – неединственность базиса
Лагранжа даже в условиях строгого соблюдения интерполяционной гипотезы.
Большинство специалистов допускает неединственность базиса, однако только при
отмене некоторых ограничений интерполяционной гипотезы. Мы не касаемся
интерполяции по Эрмиту, когда существенно изменяется сама гипотеза.
Основная часть. Чтобы сформулировать
задачу бикубической интерполяции 
, рассмотрим стандартный квадрат 
с 12 узлами,
равномерно расположенными по периметру (рис. 1).
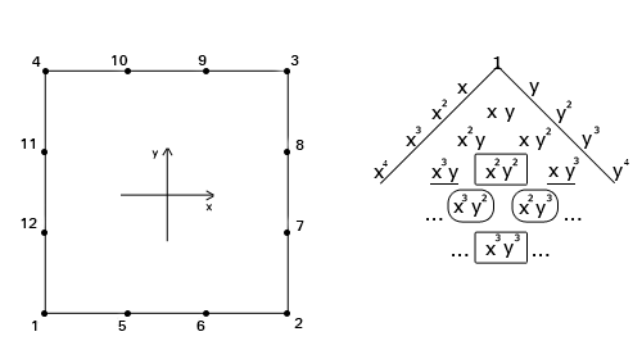
Рис.
1 Элемент Q12 и треугольник Паскаля
Пусть в
нашем распоряжении имеется массив из 36 чисел. Это координаты узлов 
, 
, а также узловые значения 
.
Требуется
восстановить 
внутри конечного
носителя, т.е. построить интерполяционный полином в форме
, (1)
где 
– базис Лагранжа.
Базис
Лагранжа – это 12 функций, обладающих следующими свойствами:
(2)
где i – номер функции; k
– номер
узла.
Задача
интерполирования сводиться к построению базиса Лагранжа. Сегодня мы знаем
несколько способов построения базисов серендипова семейства. А в начале “серендиповой” истории (1968),
Эргатудис, Айронс и Зенкевич нашли эти полиномы подбором [2]. Сразу же удалось
подтвердить результат методом обратной матрицы. В полином, содержащий 12
мономов, были включены 10 членов полного полинома 3-го порядка и два члена из
группы 4-го порядка: 
и 
(в треугольнике
Паскаля они подчеркнуты). Матрица СЛАУ 12х12 оказалась невырожденной, что укрепило
уверенность в единственности решения задачи интерполирования. Полученный базис
назвали стандартным. В 1972г. Р. Тейлор предложил нематричный метод
систематического генерирования стандартных базисов. В 1982г автор настоящей статьи
впервые построил стандартный базис геометрически. Именно геометрический метод
позволил в том же году получить первый нестандартный базис, который содержал
13-й моном: 
. Уместно отметить, что наивысшая степень не превышает 4, и
в этом смысле новый базис не отличается от стандартного. Так был развеян миф о
единственности базиса бикубической интерполяции. Ниже мы покажем функции
стандартного и альтернативного базисов. А сейчас обсудим мнения наших
предшественников относительно интерполирования 
. За 10 лет до появления серендиповых элементов Березин и
Жидков в [1] обсудили возможность возникновения альтернативных интерполянтов
функции двух аргументов. По их мнению неединственность возможна, если снять
ограничение на степень интерполянта или существенно изменить схему расположения
узлов. Зенкевич [2] подчеркивает, что единственность можно обеспечить, если
оставить в интерполянте члены возможно более низкого порядка (для Q12 это
четвертый порядок). В [4] доказано, что при нарушении этого правила сходимость
сохраняется, хотя аппроксимация несколько ухудшается. Именно такие модели
рассматривают в [3] Коннор и Бреббиа. Вместо стандартной комбинации они
предложили добавить к полному полиному 3-й степени два члена 5-й степени (в
схеме Паскаля они в кружочках) или по одному члену соответственно 4-й и 6-й
степени. (в квадратиках).
Обращает на
себя внимание строгое соответствие между количеством узлов и количеством
мономов стандартного базиса. Мы покажем, что на 12-узловом элементе существует
базис из 12-ти функций, который содержит 13 мономов. При этом на Q12 сохраняется
4-й порядок интерполянта и привычное расположение узлов (рис. 1).
Теперь
покажем базисы бикубической интерполяции: стандартный и альтернативный. Выбор
системы координат и симметричное расположение узлов (рис. 1) позволяет
ограничиться лишь двумя функциями, например, 
и 
. Из 
легко получить все “угловые”,
из 
– все “промежуточные”
функции.
Типичные функции
стандартного базиса (1968) имеют вид:
(3)
Типичные функции
альтернативного базиса (1982) имеют вид:
(4)
.
Остальные
функции базисов легко получить из (3) и (4) путём перестановки x
и y.
Основные
особенности стандартного базиса: кратные нули в узлах, отрицательные значения в
поузловом распределении нагрузки от равномерной массовой силы. Легко убедиться,
что в альтернативном базисе кратных нулей меньше, отрицательных нагрузок нет.
Главное достоинство альтернативного базиса – наличие 13-го параметра: 
. Именно этот параметр позволяет генерировать на Q12 множество
13-параметрических базисов, управляя интерполяционными качествами моделей.
Литература
1.
Березин И.С. Методы
вычислений / И.С. Березин, Н.П. Жидков. – М.:Наука, 1966. – 632с.
2.
Зенкевич О. Метод
Конечных элементов в технике / О.Зенкевич. – М.:Мир, 1975. – 541с.
3.
Коннор Дж. Метод
окнечных элементов в механике жидкости / Дж. Коннор, К.Бреббиа. – Л.:
Судостроение, 1979. – 264с.
4.
Dunne P.C. Complete polynomial displacement fields for
finite element method / P.C. Dunne. – J.Roy.Aeron.Soc., 72, 1968. – P.245-246.