Сатыбалдиев О

Касымбекова М.Т. преподаватель

Даркенбаев Д.К. магистрант

Казахский Национальный технический университет имени К.И. Сатпаева

Использование системы линейных уравнений и неравенств при решении экономической задачи

Рассмотрим конкретную экономическую задачу. Пусть предприятие располагает двумя видами ресурсов в количестве соответственно 50 и 60 единиц, из которых изготавливает два вида продукции. Стоимость единицы готовой продукции пусть будет соответственно 3 тенге и 4 тенге. Известно, что для изготовления первой продукции потребуется 2 единицы первого ресурса и 3 единицы второго ресурса, а для изготовления единицы второй продукции потребуется 4 единицы первого ресурса и 2 единицы второго ресурса. Требуется составить план производства продукции с таким расчетом, чтобы от реализации изготовленной продукции предприятие получило бы как можно больше прибыли.

Составим математическую модель поставленной задачи. Обозначим через и соответственно количество единиц готовой продукции первого и второго вида. Общая прибыль предприятия от продажи этой продукции, очевидно, будет равняться На переменные и накладываются следующие ограничения:

1) . (Это означает, что расход первого ресурса для изготовления всей продукции не может быть больше имеющегося запаса);

2) . (то же самое и для второго ресурса);

3) и . (количество изготовляемой продукции и первого и второго вида не может быть отрицательным числом).

Соединяя все вместе мы получим экономико-математическую модель поставленной задачи: найти наибольшее значение функции: при ограничениях:

Таким образом, из множества решений системы линейных неравенств необходимо подобрать такое, для которого значение целевой функции достигает наибольшего значения.

Данную задачу можно решать и используя систему линейных уравнений. Для этого система неравенств путем добавления дополнительных переменных приводится к равенствам. Итак, неравенство путем добавления новой неотрицательной переменной превращается в равенство .

Точно также неравенство добавлением новой неотрицательной переменной , превращается в равенство .

Тогда сформулированную выше задачу можно описать так: из множества неотрицательных решений системы линейных уравнений:

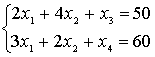
найти решение, для которого значение функции будет наибольшим.

Заметим, что оптимальное (наилучшее) решение надо искать только среди опорных решений системы ограничений, т.е. среди опорных решений заданной системы линейных уравнений.

Приступим к решению этой задачи данным способом. Ищем опорные решения системы (их, конечно, не больше числа . По ходу будем записывать получаемое опорное решение и приводить значение функции для этого решения.

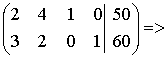
опорное решение (0; 0; 50; 60), т.е. . Значение в этой точке равно 0, т.е.

Проведя анализ таблицы, определяет комбинации возможных опорных решений.

Элемент «2» в первой строке нельзя взять в качестве разрешающего элемента, так как . Следовательно, комбинация (+; -; -; +) не соответствует опорному решению.

Элемент «4» брать можно брать в качестве разрешающего, т.е. комбинация (-; +; -; +) соответствует опорному решению.

Элемент «3» во второй строке можно брать в качестве разрешающего, т.е. комбинация (+; -; +; -) принимается.

Элемент «2» во второй строчке не подходит, т.е. комбинация (-; +; +; -) не берется.

Итак, мы выявили еще четыре комбинации базисных решений, две из которых соответствуют опорным решениям. Найдем эти решения.

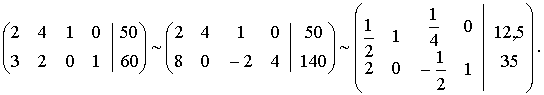
Получаем опорное решение: (0; 12; 5; 0; 35), .

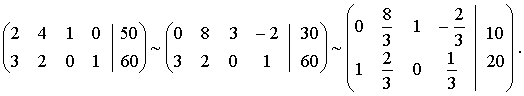
Получаем опорное решение: (20; 0; 10; 0), .

Осталось проверить последнюю комбинацию (+; +; -; -). Из матрицы

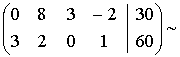
получаем, взяв в качестве разрешающего элемента число «8» из первой строки. Итак:

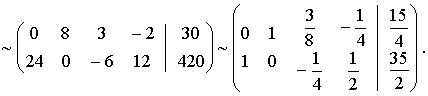
Получаем опорное решение:, .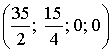

Итак, задача решена.

Литература

1. Кремер Н. Ш. Высшая математика для экономистов, М., 1997, 438 с.

2. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике, М., 1998, 365 с.

3. Абалакин Л.И. Новый тип экономического мышления, М., Экономика, 1987, 189 с.