Professor, Doctor of Sciences Korobov V.I., 
post-graduate student Gladkova E.G.
Kharkiv National University, Kharkiv, Ukraine
An algorithm for decoding of binary BCH codes
 The present can be characterized by unheard-of increase in size of data flows. This applies to almost every sphere of human activity. Thus, the issue of information transmission is becoming increasingly important. Information can be transmitted over communication channels that are affected by noise. However, in some cases, distortion of the transmitted information is unacceptable. In this connection there is the problem of obtaining accurate information despite the presence of noise in the communication channel.
 In 1948 and 1949 Shannon’s classic works appeared, which has caused a great flow of researches on the construction of efficient coding schemes for the information transmission over real channels with noise. Shannon proved that there is a coding such that the information can be transmitted with arbitrarily high degree of accuracy, provided that the transmission rate does not exceed a certain value called the bandwidth. However, Shannon's theorem is proved by the method of random selection of vectors and does not say anything about implementation of this coding.
 There are methods for construction of codes with given properties, inter alia BCH code. BCH codes were invented in 1959 by French mathematician Alexis Hocquenghem, and independently in 1960 by Raj Bose and D. K. Ray-Chaudhuri. The acronym BCH comprises the initials of these inventors' names.
 There are several methods of such codes decoding, in particular Berlekamp–Massey algorithm, Peterson–Gorenstein–Zierler algorithm and Euclidean algorithm.
 Authors suggested an algorithm for decoding of binary BCH-codes that is able to correct at least one more error than all of previously mentioned algorithms on the assumption that no more than three errors occurred, the BCH code parameters being the same. This algorithm consists in finding a solution of a polynomial system with irregular power gaps over  of the following form

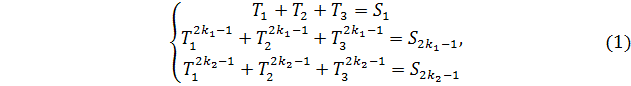
where

The method of solving of system (1) generalizes the method introduced by authors in [2] for solving of the polynomial system over of the form

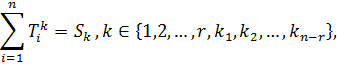
where

References

[1] Berlekamp, E. (1968). Algebraic coding theory. New York: McGraw-Hill.

[2] Korobov, V. and Gladkova, E. (2014). A method for research on polynomial systems. In: II International Conference ANALYSIS AND MATHEMATICAL PHYSICS., Kharkiv, pp.34-35.

[3] Peterson, W. and Weldon, E. (1972). Error-correcting codes. Cambridge, Mass.: MIT Press.