Кисанова М.К.

учительница математики спец. школа-интерната №1 г.Алматы

Организация учебной деятельности учащихся по ормированию и закреплению понятия функции

Перед учителями математики встает проблема отбора учебного материала с тем, чтобы обеспечить успешное изучение математики, других учебных дисциплин и успешную работу в школе. Дело в том, что задача отбора учебного материала стоит перед каждым учителем средней школы при планировке любого урока: какие упражнения, какие задачи необходимо отобрать для реализации учебных целей, как распределить материал изучаемой темы между уроками и т.д.

Одно из основных понятий в современной математике – понятие функции. Возможность выражения законов природы, связей между отдельными физическими, химическими и другими величинами через математические функции является ценным орудием научного исследования. Понятие функциональный зависимости воплощает диалектические черты современного математического мышления, приучает представлять величины в их изменчивости и взаимной связи.

Изучение функции в школе является органически составной частью процесса обучения математике. Функции являются самостоятельным объектом изучения. Им отводится важная роль и при изучении других математических понятий.

В науке нет единого подхода к определению понятия функции, что каждый этап развития функции сопровождался своим определением этого понятия, своим подходом к нему. Это можно заметить, как в историческом развитии, так и в развитии среднего и высшего образования, т.к. развитие науки всегда влечет за собой и изменение содержания обучения. Сколько бы не изменялись программы по математике, фундаментальные понятия всегда будут составлять основное содержание как школьного курса математики, так и вузовского.

Понятие функции является одним из центральных понятий математики. С приложениями элементарных функций можно столкнуться во многих областях окружающей действительности. Функция проникла во многие науки.

Мы ниже будем рассматривать упражнения, связанные с организацией учебной деятельности учащихся по формированию и закреплению понятия функции.

Первое упражнение направлено на формирование у студентов понятия функциональной зависимости. Данная задача помогает перенести понятие функции в геометрию, дает для этого подготовительный материал.

1. Находится ли площадь прямоугольника в функциональной зависимости от длины его диагонали? Находится ли радиус окружности, описанной около прямоугольника, в функциональной зависимости от длины его диагонали?

Цель следующих упражнений закрепить у учащихся само понятие функции. Эти упражнения содержат различные соответствия. Для того, чтобы выбрать среди них функции, нужно понимать, что для этого требуется однозначное соответствие.

2. Пусть А-множество выпуклых четырёхугольников на плоскости. В-множество точек этой плоскости. Выясните, какие соответствия между множествами А и В являются функциями, а такие не являются таковыми:

а) четырёхугольнику соответствует точка пересечения его диагоналей;

б) четырёхугольнику соответствует точка пересечения отрезков, соединяющих середины противоположных сторон;

в) четырёхугольнику соответствует центр окружности, не пересекающейся с его сторонами;

г) четырёхугольнику соответствует центр вписанной в него окружности;

д) четырёхугольнику соответствует центр описанной около него окружности.

3. Каждому параллелограмму сопоставляется его площадь. Является ли это соответствие функцией?

4. Каждой окружности сопоставляется касательная к ней прямая. Является ли это соответствие функцией?

5. Каждой окружности сопоставляется вписанный в неё квадрат. Является ли это соответствие функцией? Является ли функцией соответствие, при котором каждой окружности сопоставляется вписанный в неё квадрат, стороны которого параллельны осям координат?

6. Является ли функцией соответствие, при котором каждому треугольнику сопоставляется центр описанной около него окружности?

7. Возможна ли функция, у которой область определения состоит из пяти элементов, а множество значений - из семи элементов? Из четырёх элементов? Приведите примеры.

Следующее упражнение раскроет неправильное представление, часто складывающееся у учащихся в школе о том, что функция обязательно задается одной формулой.

8. Найдите

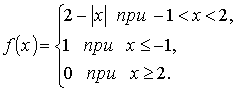
Следующие упражнения направлены на закрепление понятий области определения и множества значений функции.

9. Функция задана формулой . Найдите:

а) область определения функции ; б)

10. Функция определена на промежутке .

Найдите области определения функций

Функция определена на отрезке Каковы области определения функций:

?

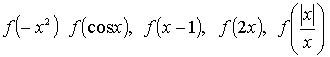11. Найдите область определения функции:

а) б)

в) г)

д) ж)

12. Найдите область определения и множество значений функции:

а) б)

в) г)

13. Периметр осевого сечения цилиндра равен 2P. Выразите объем и полную поверхность цилиндра как функцию от длина радиуса основания R и найдите область определения функции.

14. Функция задана формулой по множестве , где – множество действительных чисел, на котором выражение имеет смысл. Найдите множество .

15. Равны ли функции

а) и а) и

Учащиеся, должны понимать, что в общем случае область определения каждой функции выбирается на основе соображений либо чисто математических, либо прикладных. На это нацелено, в частности, упражнение 13.

Цель упражнения 15 – повторить понятие равенства функций, где важное значение имеют области определения рассматриваемых функций. Поэтому при решении упражнения 14, при равенстве числовых значений, следует особо обратить внимание студентов на различные области определения данных функций.

Упражнения приведенных серий помогают уточнить понятие функции, известное из средней школы, понять, что для задания функции, необходимо задать область ее определения и закон однозначного соответствия.

Литература

1. Купич В.И. Теоретические основы обучения решению школьных математических задач. Автореф.дис. докт.- М.:МП-ГУ,1992.

2. Мордкович А.Г. О профессионально-педагогической напрвленности математической подготовки будущих учителей.- М.Математика в школе, 1984, № 6.