УДК 378.6.016.02:51(574)  

 

РАЗНЫЕ МЕТОДЫ ПУТЕЙ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

Жоранова Н.Ж.,  Тулегенова С.Н

 

Так как знание является измерением и механизмом  цивилизации любая духовная и социальная степень  государства будеть зависима от степени знания. 

            Воспитание подходящего цивелизованного, все сторонне развитого наследника народа является одной из целью сегодняшней школы. Эта цель требует от каждого учителя школы ежедневного совершенствования современными  методами. Исполнение этих требований будет тогда когда каждая тема, каждая глава любого предмета будет донесена до сознания ученика. Если так то в воспитании учеников личностями предмет  математики занимает огромное и весомое место.  

Эта статья мотивирует разные методы решения квадратных уравнений предусмотренных на курсах алгебры.   

«Квадратные уравнения» одна из основных тем курса алгебры в школе. Многие природные процессы и изменения, решение содержательных примеров упирается в решение квадратных уравнений. В  случаях  решений неравенств, изучений функций (нулей функций, точек экстремум, поиске растояний возростания и убывания), решении самых больших и самых маленькиз значений возникает необходимость знания квадратных уравнений.  А также в решении методом обмена тригонометрических, указательных и логарефметических уравнений приводит к квадратным уравнениям.

В процессе изучения мы выяснили что есть возможность знакомства учеников с девять способами решения «квадратных уравнений». А именно:

1-метод. Групировать левую сторону уравнения на множители

например:       х2+4х+3 =0      решим уравнение.

 Сгруппируем левую сторону уравнения на множители:

                     х2+х+3х+3 =х(х+1)+3 (х+1) =(х+1)(х+3)

значить уравнение можно писать так:  (х+1)(х+3) =0

так как множитель равен нулю один из множителей должен быть равен нулю. Значить в левой стороне уравнения х=-1 и  числа х2+4х+3=0 будут являтся основанием уравнения.

         2-метод. Метод приведения к целому квадрату

             Например: решим уравнение х2+8х-9=0  .

Приведем к целому квадрату левую часть. Для этого пример х2+8х распишем так: 

 х2 + 8х=х2+2х4

сумма первого примера квадрат х-са, а вторая сумма двойная сумма х и 4. Для получения целого квадрата нужно прибавить 42. Тогда      х2+2х4+42=(х+4)2

теперь модифицируем левую половину уравнения. Прибавим в уравнение  42, минусуем. Получится         х2+8х-9=х2+2х4+42-9-4=(х+4)2-25

итак данное уравнение можно написать так:     (х+4)2-25=0 ,  то есть  (х+4)2=25.

Отсюда               х+4=5, х=1          или               х+4=-5, х= -9.                                                                             Ответ: 1;-9

3-метод. Решение уравнения методом  «перекидывания»                                

ах2+вх+с =0 , а ≠0  расморим квадратное уравнение. Умножим обе стороны уравнения на  а-, получим: а2х2+авх+ас=0. если отметим ах =у , х = . Если так придем к уравнению  у2+ву+ас =0. Это равно начальному уравнению. Найдем корни уранения у1, у2 – теоремой  Виет .   и так х1 =,  х2 =.

Здесь                коэффициент  а  умножим на свободный член. Поэтому этот метод называют методом  «перекидывания».

Напимер :     решим уравнение  2х2-9х+9=0 .

Решение:  перекидываем два коэффициента на свободные члены уравнения, в результате получим уравнение  у2-9у+18=0.  По теореме Виет

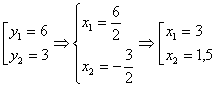                      ответ: 3; 1, 5.

            4-метод. Использование свойств коэффициентов квадратного уравнения

            ах2+вх+с=0,  а≠0 дано квадратное уравнение.       

Если  а+в+с=0  (сумма коэффициента равна нулю) , тогда х1=1, х2=

Например:  7+2-9=0 сумма равна нулю.  Составим квадратное уравнение для этих трех цифр и решим его:

                         

 

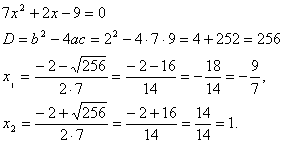
5-метод. Решение квадратного уравнения геометрическими способами

 В древние времена когда геометрия была развитие алгебры квадратные уравнения решали не алгебраическими путями а геометрическими.  Остановимся на способе решения этого уровнения у2 + 6у-16=0  древними груками.

            Решение: как указано в 4 рисунке  здесь у2+6у=16 или у2+6у+9=16+9

 у2+6у+9 и 16+9 с геометрической точки оно дает это квадрат, а начальное уравнение это тоже уравнение  у2+6у-16+9-9=0. Мы получим у+3=5 или у1=2, у2=-8.

Все указанные в статье 5 методов решения квадратного уравнения дает возможность ученикам угдубленного изучения.   Вместе с тем изучение всех методов решения квадратного уравнения пробуждает интерес учащихся к предмету.

      

 

 

Использованная литература:

 

1.      Математика, информатика, физика журналы . №5, 2003г.

2.      Брадис В.М.   четырехзнаяная математическая таблица– М.: Просвещение, 1990