Мatysina Z.A., Botsva N.P., Elina E.V., Yarochevskaya A.V.

Oles Honchar Dnipropetrovsk national university, Ukraine

THEORETICAL STUDY OF HYDROGEN-SORPTION PROPERTIES OF FULLERITE C₆₀

In terms of the increase in energy needs of humanity and the background of the deterioration of the planet's ecological situation is urgent search for alternative and clean energy. One of these sources can be hydrogen burning which is not accompanied by the release of hazardous products. It is known that reversible hydrogen sorbent that can be used for hydrogen energy needs can be fullerite F = C₆₀ [1,2].

The subject of interest of the present paper is the theoretical study of the statistical theory of lattice hydrogen solubility in fullerite C₆₀ based on the distribution of hydrogen atoms in the interstices of four various types.

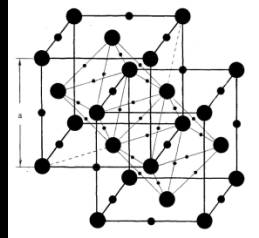
Under normal conditions fullerite C₆₀ has a face-centered cubic (fcc) lattice containing 4 units of fullerene molecules and 4 octahedral (O), 8 tetragonal (θ), 32 trigonal (Q) and 36 bigonal (D) interstices, where assumed to be placed hydrogen atoms (Fig. 1) [3].

a	b

Fig.1. Face-centered cubic unit cell of hydrofullerite C60Hx
	position of fullerene molecules and hydrogen in octahedral
and bigonal (a) and tetragonal and trigonal (b) interstitial lattice

The number of fullerene molecules in the immediate vicinity is hydrogen for different types of interstitial respectively as follows: 6 for O, 4 for θ, 3 for Q and 2 for D. Distances between adjacent pairs of fullerene-hydrogen (FH) have the following values (in nanometers):

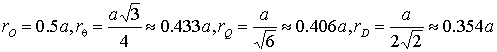, (1)

where – the fcc lattice parameter of fullerite [3].

For calculation of free energy

(2)

introduce the signs – the number of crystal (fullerene) clusters;

, , , – the number of interstices O, θ, Q, D;

, , , – the number of hydrogen atoms in interstices O, θ, Q, D, with some of interstices can be found vacant.

The full number of the hydrogen atoms in all interstices is

. (3)

The concentrations of the hydrogen atoms in interstices O, θ, Q, D with respect to the fullerene number are

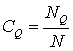, , , . (4)

The full concentration of the lattice hydrogen atoms in fullerite is

. (5)

The hydrogen atom energy in each interstice is defined by a sum of energies of it’s interaction with the nearest fullerenes

, , , , (6)

where

, , , (7)

– the energy of pair interaction of hydrogen atoms with the nearest fullerenes for interstices O, θ, Q, D.

Configurational energy E and thermodynamical probability W will be equal

(8)

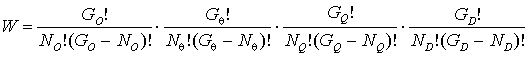(9)

Substituting (8) and (9) into (2) taking into account the Stirling formula, equitable for the big numbers, find the free energy in the form

(10)

Equilibrium states of hydrofullerite are defined from the clause of free energy minimization which is easily to find with Lagrange's method of undetermined multipliers

, ,

, , (11)

where is the chemical potential, defining the activity of hydrogen atoms, which can differ from interstices O, θ, Q, D.

Each formula, taken separately from (11), defines the temperatur dependence of hydrogen solubility in the interstices of four various types. Character of the temperature dependence each of the concentrations is difined also with energy's parameters , , , , which may be of different signs in the case of the different distances (1) in the couples of FH.

Fig.2 shows the monotonous temperature dependence of a concentration (11) for positive and negative energy values , , , . If U_i > 0 solubility increases and if U_i < 0 solubility decreases whis the temperature rise.

When comparing the calculation results with the experimental data [4] there is a quality matching the temperature dependences of the solubility of hydrogen in fullerite.

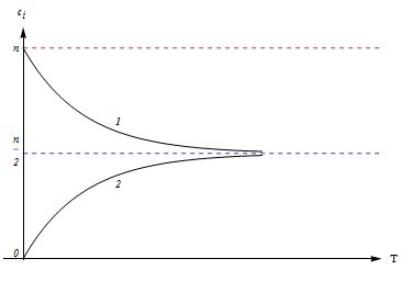
Fig. 2. Temperature dependence of a hydrogen solubility С_i

in the interstices of four various types: 1 – Ui > 0; 2 – Ui < 0;

n = 1, 2, 8, 9 for i = O, θ, Q, D

Thus the statistical theory of solubility of hydrogen in the lattice of fullerite C₆₀ considering the distribution of hydrogen atoms in the interstices of four types is developed. Calculated free energy hydrofullerite and established conditions of thermodynamic equilibrium system, which found the concentration of hydrogen atoms in all the interstices and identified similar to the experimental temperature dependence of the solubility of hydrogen atoms when placed in the interstices of various types.

References

1. Fullereny – osnova materialov budushchego / V.I.Trevilov, D.V.Shchur i dr. – K.: ADEF-Ukraina, 2001. – 48 p.

2. Atomarnyye, fullerenovyye i drugiye molekulyarnyye fazy vnedreniya / Z.A.Matisina, D.V.Shchur, S.Yu.Zaginaychenko.– D.: Izd-vo Makovets'kiy, 2012. – 888 p.

3. Rastvorimost' primesey v metallakh, splavakh, intermetallidakh, fulleritakh / Z.A.Matisina, S.Yu.Zaginaychenko, D.V.Shchur. – D.: Nauka i obrazovaniye, 2006. – 514 p.

4. Savenko A.F. Osobennosti gidrirovaniya fullerita C₆₀. Avtoreferat kand. diss. – K.: KIM, 2013. – 20 p.