УДК
624.078.54
Бондаренко Л. М., Яковлєв С. О., Крамар І.Е., Шаптала О. І.
Дніпропетровський національний
університет залізничного транспорту ім. акад. В. Лазаряна
Умови кочення
без проковзування тіл при різних схемах дотику
Вступ. При перекочуванні однієї
прямолінійної поверхні по іншій виникає деякий опір, який називається тертям
другого роду, або тертям кочення. Як і тертя ковзання, тертя кочення являє
собою складне явище.
В
місці дотику, наприклад, циліндра з площиною при силі тертя F, вона при відсутності ковзання повинна задовольняти
умові 
, де 
- це коефіцієнт
тертя(зчеплення); 
- нормальний тиск.
Якщо
сила, яку необхідно прикласти до середини циліндра для подолання опору кочення
Р, то при 
коток в місці дотику буде «утримуватись» і відбудеться кочення.
Навпаки якщо величина сили 
де 
- коефіцієнт тертя кочення; 
- плече сили Р,
по віношенню до точки через яку необхідно перекотити циліндр,
більше 
то кочення неможливе. Циліндр буде ковзати по площині, тому, що
рух відбувається в напрямку меншого опору.
Таким
чином, умовно кочення буде (рис. 1)
(1)
або
(2)
Якщо
рушійна сила Р, прикладена до центру циліндра, з достатньою точністю може
прийняти 
і
або
Якщо
рушійна сила прикладена не в центрі циліндра, а на відстані 
, то
Якщо ж рушійна сила
прикладена по дотичній до утворюючої циліндра, то
Не зупиняючись на
фізичній сутності опору тертя кочення наведемо формулу коефіцієнта тертя
кочення, запропоновану в [1]
де
- це ширина плями контакту; 
- коефіцієнт, який залежить
від пружності після дії в матеріалах тіл контакту.
Нажаль
автор не дає рекомендацій щодо вибору цього коефіцієнта і таким чином не
можливо теоретично отримати формулу (2)
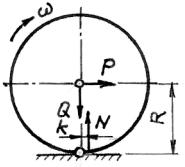
Рис. 1. До визначення явища
кочення без проковзування.
В
[2] отримані формули для визначення коефіцієнта тертя кочення, які утримують
загально прийняті механічні константи контактуючих при коченні тіл і їх геометричні розміри.
Виклад основного матеріалу.
При
початковому лінійному контакті в [2] наведені такі формули:
при початковому лінійному контакті
(3)
де b – це півширина плями контакту, яка визначається із теорії контактних деформацій
Герца [3]; R –
радіус в метрах при початковому точковому контакті
(4)
В
подальшому розглянемо найбільш вживані на практиці схеми дотику.
1
Схема дотику циліндр-площина.
Півширина плями контакту
(5)
де В – довжина циліндра, Е – модуль
пружності матеріалів циліндра і площини
Звичайно,
що радіус циліндра і площини необхідно взяти таким, щоб контактні напруження
дорівнювали допустимим, тобто
. (6)
Тепер
формула (3) може бути записана у вигляді
(7)
а формула (2) приймає вигляд
(8)
При,
наприклад, Q=50 кН, В=40мм, 
=500 МПа і Е=2,1
МПа, R=184мм,
k=0,29 мм, а 
. При величині допустимих
напружень 
=500 МПа, R=56.7 мм і 
. Реальне значення 
для сталей 
[4]
Недивлячись на пряму
залежність (8) від 
і Е величина 
не підкоряється такій залежності внаслідок присутності
експонентності, яка визначає коефіцієнт гістерезисних витрат [2].
2. Схема
дотику сферичне тіло і площина
Радіус
сферичного тіла(кулі)
(9)
Півширина
плями контакту
(10)
Коефіцієнт
тертя кочення
(11)
Умова
кочення без проковзування
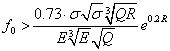(12)
Оскільки
при точковому контакті величина при допустимих контактних напружень в
середньому в 1.4 раз вища, чим при лінійному, то приймемо замість 
=500 МПа в попередньому
прикладі 
=700 МПа а замість 
=900 МПа величина 
=1260 МПа.
Радіус
кулі для першої величини 
складає R=420
а для другої R=254 мм.
Умова
кочення без проковзування для першого випадку 
а для другого 
.
3.1 Роликовий підшипник (зовнішнє кільце-шарик)
Радіус
ролика
(13)
де 
- радіус поверхні кочення
зовнішнього кільця.
Півширина плями контакту
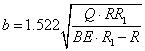(14)
Коефіцієнт
тертя кочення
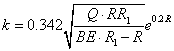(15)
Умова
кочення без проковзування
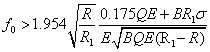(16)
При 
=60 мм, величина 
складає: при 
=500 МПа 
0,0061, а при 
=900 МПа 
0,0033.
3.2
Куля і циліндричний жолоб
Радіус
кулі
(17)
де 
- це коефіцієнт, який
залежить від рівняння еліпса дотику(А/В=
); 
/R; 
- радіус жолоба
Особливістю
рішення рівняння (17) є та, що коефіцієнт m теж залежить від радіуса R.
Звичайно, що необхідно задатись величиною m і на практиці вона на небагато перевищує одиницю (m=1.03…1.05)
Півширина
плями контакту
(18)
Коефіцієнт тертя кочення
(19)
При 
=900 МПа радіус кулі
складає R=10.8 мм, а при 
=1260 Мпа R=65 мм; півширина плями контакту відповідно складає b=0.837 і 0.708 мм. Коефіцієнт тертя кочення k=0.137 і k=0.115
мм.
Умовою
кочення без проковзування буде відповідно 
0,00127 і 
0,00176.
Аналогічно
знаходиться умови кочення без проковзування для інших схем дотику.
Аналіз
отриманих підрахунків показує, що для сталей умова кочення без проковзування
виконується при любому змащенні поверхонь кочення (дійсна величина 
на порядок вища
отриманих), але для других матеріалів така перевірка необхідна.
УДК 624.078.54
Умови
кочення без проковзування тіл при різних схемах дотику (Бондаренко Л.М.)
Отримані
аналітичні залежності для визначення умови кочення без проковзування для схем
дотику циліндр – площина, сферичне тіло – площина, куля - циліндричний жолоб.
Доведено, що для сталей умова позначена без проковзування виконується при
любому змащенні поверхонь кочення, а для других матеріалів така перевірка
необхідна.
Література
1.Колчин Н. И., Мовмин М. С.
Теория механизмов и машин. – Л.: Судпромгиз, 1962 – 616с.
2.Бандаренко Л. М.
Аналітично-експерментальне визначення коефіцієнта тертя кочення/ Будівництво
України, №5, 2001. – с.47-48
3.Справочник по
сопративленюи материалов /Писаренко Г. С., Яковлев А. П., Матвеев В. В. – Киев:
Наук. Думка,1988 – 736с
4.Справочник по кранам: В 2
т. Т.2/Александров М. П., Гохберг М. М., Ковин А.А. и др. – Л.: Машиностроение,
1988. – 559с.