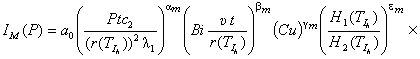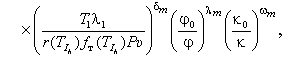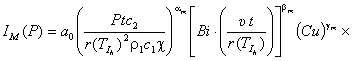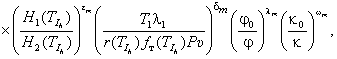Технические науки/4. Транспорт

О. А. Сидоров, В. М. Филиппов, С. А. Ступаков, А. А. Орлов

Омский государственный университет путей сообщения, Россия

ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ МЕХАНИЧЕСКОГО ИЗНАШИВАНИЯ КОНТАКТНЫХ ПАР УСТРОЙСТВ ТОКОСЪЕМА

Контактная пара системы токосъема электрического транспорта (контактная вставка – контактный провод) представляет собой электрический скользящий контакт, элементы которого функционируют в условиях износа, обусловленного механической и электрической составляющими процесса токосъема, а также многими другими факторами условий эксплуатации: родом и силой тока, температурой элементов контактной пары, параметрами внешней среды и т. п. Одним из путей повышения срока службы элементов контактных пар устройств токосъема является подбор наиболее отвечающих требованиям качества токосъема материалов. В Омском государственном университете путей сообщения разработана методика [1] экспериментальных исследований изнашивания контактных пар устройств токосъема.

Реализация методики требует наличия специализированных экспериментальных комплексов, а также значительных затрат времени и ресурсов. Для сокращения объема экспериментальных исследований может быть использован комбинированный способ – совокупность необходимого минимума экспериментальных исследований реальных объектов (или их аналогов) и методов расчета, основанных на математическом моделировании процессов, происходящих в контактных парах устройств токосъема.

Контактная пара устройств токосъема как монорельсового, так и магистрального электрического транспорта представляет собой узел, который функционирует в условиях электромеханического изнашивания. В соответствии с этим развитие математической модели взаимодействия элементов контактной пары «контактный элемент – токопровод» (КЭ – Т) и «контактная вставка – контактный провод» (КВ – КП) осуществлялось по двум направлениям [2, 3]: для моделирования механического износа (от нажатия в контакте) и для моделирования электрического износа (от токовой нагрузки).

Ввиду неоднородности составляющих процесса электромеханического изнашивания контактных пар устройства токосъема электрического транспорта необходимо составлять соответствующие модели для механического (от нажатия в контакте) и электрического (от токовой нагрузки) изнашивания [4].

Уравнение для решения задачи об оптимальных условиях механического изнашивания при поиске области оптимума приведено в работе [5]. В этом уравнении в соответствии с положениями теории подобия в комплексы и симплексы были объединены следующие факторы: нажатие в контакте, удельная теплоемкость, теплопроводность – комплекс; скорость скольжения, время испытания – комплекс; твердости элементов пары трения – симплекс.
В качестве параметра оптимизации принята интенсивность механического изнашивания I_М.

Функциональная зависимость между I_М и факторами модели имеет вид:

(1)

где Р – нажатие в контакте; υ – скорость скольжения; t – время испытаний;
r –характерный линейный размер; Cu – содержание меди в КЭ; Н₁/Н₂ – безразмерный симплекс (отношение твердости материала КЭ к твердости материала токопровода); , – теплопроводности материалов КЭ и токопровода соответственно; с₁, с₂ – удельные теплоемкости КЭ и токопровода соответственно.

Зависимость (1) может быть использована и для контактной пары КВ – КП. В этом случае факторы модели отражают физико-механические параметры контактной вставки и контактного провода.

Для каждого фактора в уравнении (1) определяются показатели степени, а затем факторы с одинаковыми степенями объединены в комплексы [5]:

(2)

Из уравнения подобия (2) можно получить расчетное уравнение, коэффициенты которого определяются экспериментально. Уравнение (2) можно представить как сплошной ряд, рассматривая только первый член этого ряда:

(3)

где а₀ – функционал, отражающий влияние на процесс неучтенных факторов; – функционал, логарифмически зависящий от нажатия в контакте; , , – коэффициенты, определяемые экспериментально; Ptc₂ / (r²) – комплекс (мера отношения удельной мощности трения к способности токопровода накапливать, а контактного элемента – передавать тепло); υt / r – комплекс (отношение пути трения к характерному линейному размеру элемента).

Сравнение результатов расчета (уравнение (3)) интенсивности механического изнашивания КЭ монорельсового транспорта и КВ магистрального электроподвижного состава (ЭПС) с экспериментальными данными показывает, что расхождение составляет 9 %. Изменение параметров окружающей среды (увеличение относительной влажности воздуха до 98 %, а запыленности – до 200 мг/м³) повышает значение относительной погрешности до 20 % [1].

Для повышения точности расчета износа КЭ и КВ в модель были внесены критерии, позволяющие учитывать изменение влажности и запыленности окружающей среды. Кроме этого, многие авторы доказали влияние температуры элементов контактной пары на их твердость и, как следствие, на фактическую площадь контакта. В связи с этим в уравнение (3) также добавлен критерий, позволяющий учитывать влияние силы трения в скользящем контакте на износ элементов контактной пары.

В связи с этим уравнение (3) примет вид:

,

(4)

где – критерий Мейера; Pυ – мощность трения, f_т – коэффициент трения;– отношение среднего значения относительной влажности окружающей среды за пять лет к значению относительной влажности на момент исследований, – отношение среднего значения запыленности окружающей среды за пять лет к значению ее запыленности на момент исследований.

Дальнейшее развитие модели обусловлено необходимостью учитывать в модели влияние температуры элементов контактной пары на их твердость и на фактическую площадь контакта. Таким образом, уравнение (4) с учетом температуры элементов контактной пары можно записать в виде:

(5)

где 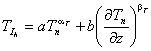– коэффициент влияния температурного градиента на интенсивность изнашивания (a, b – коэффициенты, характеризующие тепловые свойства материалов; – коэффициенты, характеризующие тепловые процессы при взаимодействии элементов контактной пары; определяются экспериментально);

Т_n – температура исследуемого n-го тела;

– градиент температуры элемента контактной пары по нормали z к его поверхности.

Теплопроводность материала КЭ:

,

(6)

где , – плотность и температуропроводность материала соответственно.

Тогда

(7)

где 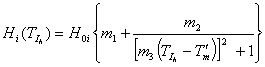– твердость материала элемента контактной пары в зависимости от его температуры [6];

– то же при нормальной температуре;

m₁, m₂, m₃ – константы материала;

– температура, при которой принимает максимальное значение;

– критерий Био, устанавливающий соответствие между интенсивностью теплообмена и распределением температуры в твердом теле;

– перепад температуры по объему КЭ;

– температурный напор (разность температур материала КЭ и окружающей среды).

Номограммы и диапазоны изменения коэффициентов и функционалов для расчета по модели (7) приведены в работе [1].

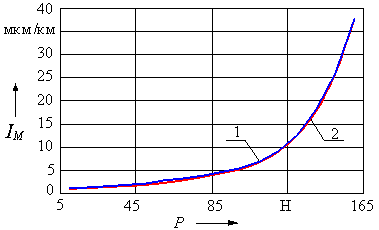
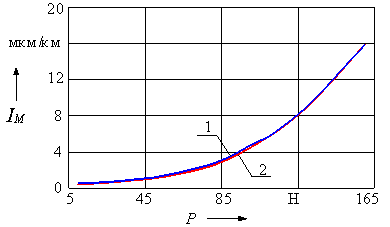
На рис. 1 приведены графики механического изнашивания контактных элементов, полученные экспериментально и в результате расчета на модели (уравнение (7)), для контактных вставок из графита и металлокерамики токоприемников магистрального ЭПС. Графики получены при нормальных условиях окружающей среды [7] (температура окружающего воздуха + 23 ^оС, относительная влажность 50 %, запыленность 3 мг/м³). На рис. 1 и 2 приняты обозначения: 1 – результаты эксперимента; 2 – результаты расчета по формуле (7). Расхождение расчетных и экспериментальных данных составляет 6 %.

а

б

Рис. 1. Интенсивность изнашивания КВ магистрального ЭПС: а – КВ из графита; б – КВ из МК-Ж

Анализ графиков на рис. 1 позволяет сделать заключение о возможности использования формулы (7) для моделирования механической составляющей изнашивания КЭ и КВ. Однако заключение о трибосовместимости и задиростойкости материалов контактной пары можно сделать только на основании результатов экспериментальных исследований.

Таким образом, на основании анализа особенностей условий эксплуатации контактных пар устройств токосъема, экспериментальных данных и существующих математических моделей изнашивания обоснована возможность разделения модели электромеханического изнашивания на две модели (модель механического изнашивания (от нагрузки в контакте) и модель электрического изнашивания (от токовой нагрузки), и разработана математическая модель механического изнашивания элементов контактной пары устройств токосъема монорельсового и магистрального электрического транспорта, которая позволяет учитывать влияние на механическую составляющую износа параметров окружающей среды (влажности и запыленности), а также температуры материалов элементов контактной пары.

Литература:

1. Ступаков, С. А. Моделирование электромеханического изнашивания контактных пар устройств токосъема электрического транспорта / С. А. Ступаков, О. А. Сидоров, В. М. Филиппов // Трение и смазка в машинах и механизмах. – М.: Машиностроение, 2012. – № 4. – С. 23 – 30.

2. Biesenack, H. Kontakt zwischen Fahrdraht und Schleifleiste–Ausgangspunkte zur Bestimmung des elektrischen Verschleißes / H. Biesenack, F. Pintscher // Elektrische Bahnen. – München: Oldenbourg Industrieverlag GmbH, 2005. – № 3. – P. 138 – 146.

3. Кончиц, В. В. Триботехника электрических контактов / В. В. Кончиц,
В. В. Мешков, Н. К. Мышкин. – Минск: Наука и техника, 1986. – 260 с.

4. Крагельский, И. В. Основы расчетов на трение и износ / И. В. Крагельский, М. Н. Добычин, В. С. Комбалов. – М.: Машино-строение, 1977. – 499 с.

5. Браун, Э. Д. Моделирование трения и изнашивания в машинах / Э. Д. Браун, Ю. А. Евдокимов, А. В. Чичинадзе. – М.: Машиностроение, 1982. – 191 с.

6. Чичинадзе, А. В. Трение, износ и смазка / А. В. Чичинадзе. – М.: Машиностроение, 2003. – 576 с.

7. ГОСТ 8.050-73. Нормальные условия выполнения линейных и угловых измерений. – М.: Издательство стандартов, 1988. – 14 с.
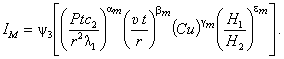
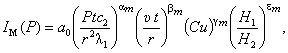
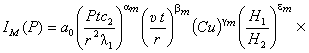
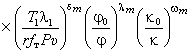