УДК 517.532: 661.9.02
Исмаилов Б.Р., Урматова А., Манекеева
Ж., Шоныкбаева Н.
Южно-Казахстанский государственный
университет им. М. Ауезова (г.Шымкент, Казахстан), Международный
Казахско-Турецкий университет им. Х.А. Яссави (г.Туркестан, Казахстан)
Математическое
моделирование гидродинамики в контактных устройствах массообменных аппаратов в
ламинарном режиме на основе уравнений Навье-Стокса
Конструкции
современных массообменных аппаратов, предназначенных для физической и
химической обработки газов и жидкостей достигли высокой степени совершенства.
При разработке методов математического моделирования потоков в их контактных
устройствах используются научные достижения механики жидкостей и газа, химии и
химической технологии, прикладной математики, физики новых явлений, а также
современные компьютерные технологии.
Теоретические и экспериментальные работы по изучению гидродинамики и тепломассообмена в аппаратах с многоступенчатым взаимодействием фаз показали наличие общих закономерностей образования и взаимодействия вихрей при обтекании дискретно расположенных элементов или контактных устройств /1/. В рабочей зоне таких аппаратов происходит сложное взаимодействие фаз, включающее прямоточное, противоточное, перекрестное, вихревое, пульсационное и другие виды движения потоков даже в пределах одной контактной ступени.
Форма и расположение конструктивных элементов контактных устройств определяют структуру двухфазного потока, характер и интенсивность воздействия вихрей на жидкость (в виде плёнок, струек и капель), поверхность межфазного контакта, диссипацию энергии, и, следовательно, эффективность процессов тепло- и массообмена. Однако, в проведённых исследованиях каждой конструкции превалируют экспериментальные или упрощённые эмпирические подходы, которые не позволяют находить скорость, завихренность, кинетическую энергию, масштаб турбулентных пульсаций и массообменные характеристики по всей зоне контактирования фаз. Недостаточно количество теоретических исследований по описанию процесса контактирования газа и жидкости в совокупности с задачами гидродинамики, теплообмена и массообмена.
Одним из основных методов моделирования динамики потоков в контактных устройствах является прямое применение уравнений Навье-Стокса /2/. Решение этих уравнений с приемлемой точностью позволяет получить распределение основного параметра, во многом определяющего гидродинамическую обстановку в аппарате - компоненту скорости. При этом аналитическое, приближенно-аналитическое или численное решение возможно с учетом геометрии контактного устройства, режима течения и других исходных данных. Следует отметить, что в последние годы появились достаточно эффективные численные методы, применимость которых для широкого класса задач показана на примере решения разнообразных важных и сложных задач теоретических основ химических технологий /3/.
В настоящей работе приведены результаты реализации математической модели движения газа в канале прямоугольной формы на основе применения уравнений Навье-Стокса и подхода /2/.
Основные уравнения. Плоское течение несжимаемой ньютоновской вязкой жидкости с постоянными свойствами при отсутствии внешних сил моделируется двумя уравнениями сохранения количества движения и одним уравнением неразрывности:
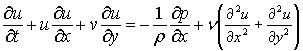 (1)
(1)
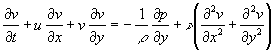 ,
(2)
,
(2)
![]() . (3)
. (3)
Уравнения
записаны в неподвижной эйлеровой системе, относительно которой движется газ
(жидкость).
Введя функцию напряженности вихря (в дальнейшем -завихренность) по
формуле
![]() , (4)
, (4)
получаем
уравнение переноса вихря, имеющее параболический тип:
![]() (5)
(5)
Введем
также функцию тока соотношениями
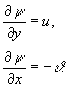 (6)
(6)
Уравнение
для ![]() можно
записать как уравнение Пуассона, имеющее эллиптический тип:
можно
записать как уравнение Пуассона, имеющее эллиптический тип:
![]() (7)
(7)
Таким
образом, система (1)-(3), записанная в терминах «скорость-давление» может быть
записана также в терминах «функция тока - вихрь» (форма Гельмгольца):
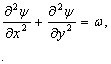 (8)
(8)
![]() (9)
(9)
Влияние многоступенчатости контактного устройства. В аппаратах /1/ контактные устройства имеют многоступенчатую форму, образованную периодическим расположением нескольких дискретных элементов по высоте. Значит, контактное устройство может быть представлено в виде совокупности начального и стабилизированного участков, причем длина стабилизированного участка оказывается гораздо больше длины начального участка (рис.1.). Длина начального участка зависит от формы входного профиля (прямоугольная, трапециевидная, параболическая и т.д.). Например, при противотоке жидкость стекает вниз через распределительные устройства, обеспечивающие достаточную равномерность и существует определенное расстояние, после которого ее распределение можно считать установившемся.
![]()
![]()
![]()
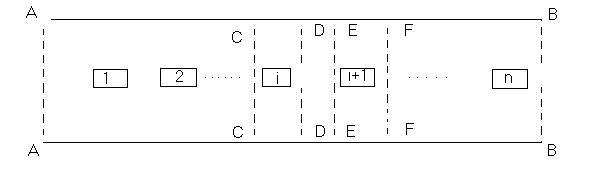
Ось абцисс-продольное направление, ось
ординат- поперечное направление к потоку,
1,2,…,n- обтекаемые
элементы.
Рисунок
1
Поток, входя в канал (сечение А-А),
движется в продольном направлении, обтекая на своем пути регулярно
расположенные элементы контактной зоны
1,2,…n
. С течением достаточного большого времени Т,
за которое поток, развиваясь в своем течении, обтекает несколько элементов, все
гидродинамические характеристики установятся. На участке А-С динамические, и соответственно - массообменные характеристики
меняются быстро, причем длина стабилизированного участка С-В гораздо больше, чем А-С.
В данном случае можно говорить об установлении по скорости и завихренности
начиная с элемента i с некоторой точностью ![]() . В этом случае основными уравнениями
математической модели являются уравнения Навье-Стокса с соответствующими
граничными и начальными условиями, а также с условиями сопряжения:
. В этом случае основными уравнениями
математической модели являются уравнения Навье-Стокса с соответствующими
граничными и начальными условиями, а также с условиями сопряжения:
![]() , (10)
, (10)
где ![]() - коэффициент уменьшения, зависящий от
разброса общего расхода газа;
- коэффициент уменьшения, зависящий от
разброса общего расхода газа;
![]() - кривая, которую можно считать линией
симметрии между двумя рядами потоков, обтекающих 2 ряда элементов насадок;
- кривая, которую можно считать линией
симметрии между двумя рядами потоков, обтекающих 2 ряда элементов насадок; ![]() - функция, в общем случае получаемая
трехточечной аппроксимацией граничного условия
- функция, в общем случае получаемая
трехточечной аппроксимацией граничного условия ![]() для
функции завихренности.
для
функции завихренности.
При обтекании первой и последней
гирлянды влияние твердых стенок канала моделируем условиями прилипания ![]() а для
вихря
а для
вихря ![]() воспользуемся
условием непротекания газа на границе канала или разделяющей линии
воспользуемся
условием непротекания газа на границе канала или разделяющей линии
![]() (11)
(11)
Некоторые точные решения уравнений
Навье-Стокса. Для несжимаемой жидкости
имеются точные решения для установившихся течений: в плоском канале при
заданном постоянном перепаде давления (течение Пуазейля); между двумя
параллельными плоскими стенками, одна из которых покоится, а другая движется в
своей плоскости с постоянной скоростью (течение Куэтта); в прямолинейной трубе
с круглым поперечным сечением при постоянном перепаде давления (течение Хагена-
Пуазейля). Также получены приближенные аналитические решения, основанные на
упрощающих предположениях. Здесь следует отметить решения при очень малых
числах Рейнольдса, соответствующие так
называемым ползущим движениям. Для решения задач динамики вязких жидкостей и
газов в каналах массообменных аппаратов при умеренных числах Рейнольдса,
соответствующих ламинарному движению, разработаны эффективные алгоритмы,
основанные на использовании разностных схем. Для задачи течений жидкостей в
областях простой формы (или около тел простой формы) нами использован разностный
метод для уравнений в форме (7-8), хотя для этой системы и имеются трудности,
связанные с определением граничных условий для завихренности.
Условия
устойчивости. Применим метод гармонических
возмущений Фурье для исследования устойчивости
схемы установления для уравнения функции тока /4/. Из теории
дифференциальных уравнений известно, что частные решения имеют следующий вид:
![]() . (12)
. (12)
Сеточным аналогом
решений вида (12) являются числа,
образованные по формуле: ![]() ,
,![]() (13)
(13)
где ![]() - постоянные числа, m,k,n-индексы сеточных узлов,
- постоянные числа, m,k,n-индексы сеточных узлов, ![]() шаги разностной
сетки. Ограниченность возмущений вида (13)
при бесконечном убывании шагов сетки является необходимым условием
устойчивости разностной схемы.
Допустим, что Re<1,
тогда значения
шаги разностной
сетки. Ограниченность возмущений вида (13)
при бесконечном убывании шагов сетки является необходимым условием
устойчивости разностной схемы.
Допустим, что Re<1,
тогда значения ![]() , характеризующие завихренность потока в рассматриваемой области течения также малы.
Согласно методу Пасконова /4/ получим, что разностная схема
, характеризующие завихренность потока в рассматриваемой области течения также малы.
Согласно методу Пасконова /4/ получим, что разностная схема
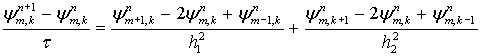 (14)
(14)
устойчива, если ![]() где
где ![]() . По аналогии с одномерным случаем, положим
. По аналогии с одномерным случаем, положим ![]() =0 и рассмотрим возмущение специального вида:
=0 и рассмотрим возмущение специального вида: ![]() , (15)
, (15)
где
![]() - вещественные произвольные числа. Подставляя (15) в (16), получим:
- вещественные произвольные числа. Подставляя (15) в (16), получим:
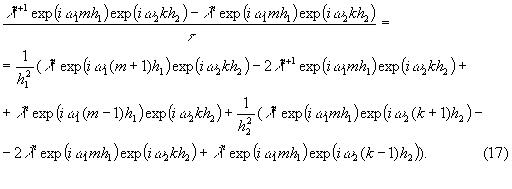
Сокращая на ![]() , получим соотношение:
, получим соотношение:
![]() (18)
(18)
Условие
Неймана для устойчивости гармонических возмущений при
![]() (19)
(19)
дает
неравенство ![]() (20)
(20)
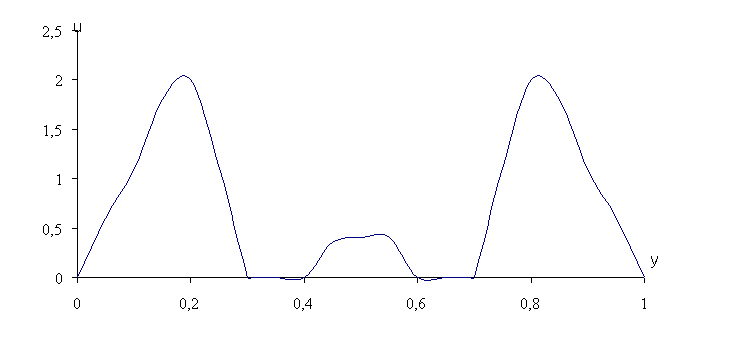 На рис.2. показано распределение продольной составляющей скорости в канале,
полученное реализацией модели (8-9) при числах Рейнольдса 10-500. Видно, что
при обтекании треугольной платины у острых симметричных углов возникают
максимальные скорости из-за сгущения линий тока, в центре канала-застойные
зоны, с обратными течениями. Дальнейшее увеличение числа Рейнольдса к
расходимости, схемы, связанное с нарушением условия (20).
На рис.2. показано распределение продольной составляющей скорости в канале,
полученное реализацией модели (8-9) при числах Рейнольдса 10-500. Видно, что
при обтекании треугольной платины у острых симметричных углов возникают
максимальные скорости из-за сгущения линий тока, в центре канала-застойные
зоны, с обратными течениями. Дальнейшее увеличение числа Рейнольдса к
расходимости, схемы, связанное с нарушением условия (20).
Рис.2. Распределение продольной составляющей скорости при обтекании
треугольной платины в прямом горизонтальном канале, стабилизированный участок, y-расстояние от нижней стенки, u- продольная составляющая скорости, Re =200.
Литература
1. 1. Балабеков
О.С. Гидродинамика, массообмен и пылеулавливание при противоточных и прямоточных двухфазных капельных и пленочных течениях
в слое подвижной насадки: Автореф. дис. докт. –М., 1985.-40с.
2. Пасконов
В.М., Полежаев В.И., Чудов Л.А. Численное моделирование процессов тепло- и
массообмена.-М.: Наука,1984.-284с.
3.
Дзюбенко Б.В., Кузма-Китча Ю.А., Леонтьев А.И., Федик
И.И., Холпанов Л.П. Интенсификация тепло-и массообмена на макро-, микро-и
наномасштабах. М.:ФГУП «ЦНИИАТОМИНФОРМ», 2008. -530с.