Ж.Б. Бакиров, Г.Д. Таженова, А.С. Солонуха

Карагандинский государственный технический университет

Виброзащита механизмов с учетом упругости звеньев

При решении задач виброзащиты оборудования источник и объект часто рассматривают как абсолютно твердые тела, соединенные между собой виброизоляторами. В действительности вынуждающие силы возбуждают не только перемещения источника и объекта как твердых тел, но и их упругие деформации.

При исследовании упругих колебаний источник и объект можно в большинстве случаев рассматривать как упруговязкие системы с конечным числом степеней свободы, малые колебания которых вблизи устойчивого положения равновесия описываются линейными дифференциальными уравнениями Лагранжа второго рода:

, (1)

где А, В, С - симметричные положительно-определенные nn - матрицы, составленные соответственно из инерционных, диссипативных и квазиупругих коэффициентов; q- n-мерный вектор обобщенных координат системы; Q(t) — вектор обобщенных сил, действующих на источник или объект.

Удобной формой описания свойств линейного объекта в условиях вибрационных воздействий являются операторы динамической податливости l_ВA (p), связывающие силу G_B (t), приложенную в заданном направлении в точке В объекта с проекцией перемещения точки А на некоторое направление

.

Обратные операторы называются операторами динамической жесткости.

Пусть источник вибрации соединен с объектом виброзащиты несколькими виброизоляторами При гармонических воздействиях , (j=1,…k), имеющих частоту , в точках крепления виброизоляторов к объекту возникают гармонические силы , направленные по осям виброизоляторов и приложенные к объекту. Эти силы вызывают гармонические колебания точек - . По принципу суперпозиции для комплексной амплитуды перемещения точки можно записать

Введем в рассмотрение матрицу динамических податливостей объекта размерности , элементами которой являются податливости .

Тогда справедливо следующее векторное выражение:

(2)

где ,- s-мерные векторы комплексных амплитуд перемещений и сил в точках крепления объекта и виброизолятора.

Аналогичным образом вводится матрица динамических податливостей источника в точках крепления виброизоляторов , связывающая комплексные амплитуды перемещений и сил в точках источника:

(3)

Матрицы, обратные введенным:

, (4)

назовем матрицами динамических жесткостей объекта и источника в точках крепления виброизоляторов.

Комплексные амплитуды сил, действующих на источник и объект в точках крепления m-ного виброизолятора, можно выразить через комплексные амплитуды перемещения этих точек следующим образом:

(5)

где - элементы матрицы динамической жесткости m-ного виброизолятора в точках крепления к источнику и объекту.

Вводя в рассмотрение четыре диагональные матрицы размерности

можно записать следующее векторное соотношение:

()

Об эффективности виброзащиты можно судить путем сравнения этих сил в объекте () с силами, которые возникли бы в нем при замене виброизолятора жесткими стержнями, прикрепленными к объекту и источнику шарнирно (). В работе [1] показано, что эти векторы связаны соотношением:

,

где комплексная матрица

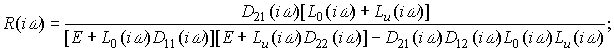(6)

Е – единичная матрица размерности .

В качестве количественной оценки эффективности виброзащиты можно выбрать какую-либо норму матрицы .

Если виброизоляторы имеют такую конструкцию, что их реакции связаны с перемещениями точек крепления соотношениями

(7)

то имеем

; ,

где диагональная матрица

Тогда 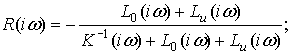(8)

Если объект и источник соединены одним виброизолятором, то становится комплексным числом, определяемым из (6) заменой на . Его модуль может служить количественной характеристикой эффективности виброизоляции. Если виброизолятор обладает свойством (7), что часто встречается, то коэффициент виброизоляции на данной частоте равен

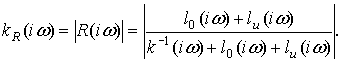(9)

Если объект или источник считать «жестким», то соответствующая матрица податливостей принимается нулевой.

В качестве объекта виброзащиты рассмотрим двухмассовую динамическую модель машинного агрегата (рисунок 1), в котором под J будем понимать приведенный момент инерции механической передачи, а под «с» и «b» при необходимости учета упруго-диссипативных свойств передачи надо понимать также их приведенные значения. В качестве источника вибрации примем исполнительный орган, который считаем жестким. Между ними разместим виброизолятор в виде упругой муфты.

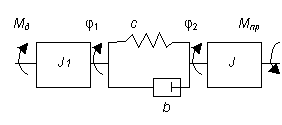
Рисунок 1 - Двухмассовая модель машинного агрегата

Определим динамическую податливость объекта . При учете статической характеристики двигателя уравнение колебаний объекта имеет вид [2]

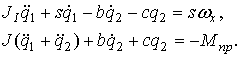(10)

где

Отсюда определяем матрицы в векторном уравнении (1):

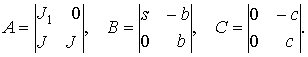
При гармоническом воздействии это уравнение имеет решение

Из выражения (2) заключаем

Так как виброизолятор прикреплен к массе с обобщенной координатой , то

где и - элемент и определитель матрицы D.

После вычисления находим

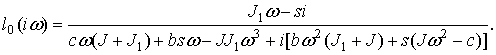
Эта же податливость получена из в работе[2].

Для линейного виброизолятора в виде упругой муфты

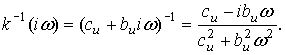
Тогда по формуле (9) коэффициент виброизоляции с учетом будет равен:

.

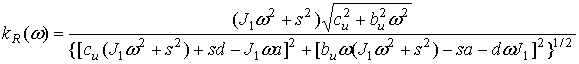В общем случае (), вводя обозначения

(11)

для такого виброизолятора можно записать

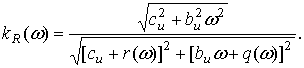(12)

При малой диссипации в системе коэффициент виброизоляции принимает наибольшее значение (виброизоляция наименее эффективна) на частотах , определяемых из уравнения

(13)

Эти частоты называются резонансными. Достаточное условие эффективности виброизоляции на этих частотах

(14)

Литература

1. Коловский М.З. Автоматическое управление виброзащитными системами. М.: Наука, 1976. 317с.

2. Бакиров Ж.Б., Ералин А.Н., Таженова Г.Д. Исследование двухмассовой модели привода с упругой муфтой. // Труды университета. Вып.3. Караганда, 2006. с. 50-53.