*99737*

Об алгоритмах метода штрафных функций с неполной минимизацией вспомогательных функций

 

Исавнин Алексей Геннадьевич, профессор кафедры «Математическое моделирование и информационные технологии в экономике», доктор физико-математических наук, профессор.

Хамидуллин Марат Раисович, соискатель ученой степени кандидата физико-математических наук.

Камская государственная инженерно-экономическая академия, г. Набережные Челны, Республика Татарстан, Россия.

isavnin@mail.ru

 

 

Целью математического программирования является разработка методов нахождения наименьшего значения функции  на множестве D, т.е. нахождения числа

 ,                                             (1)

или точки, в которой значение (1) достигается. Задача отыскания минимума некоторой функции f(x) - один из основных вопросов теории оптимизации, она эквивалентна задаче отыскания максимума той же функции, взятой с отрицательным знаком [1, стр.9]. Существует множество различных методов и их модификаций для нахождения минимума функции. В данной работе рассматривается метод штрафных функций. В основе этого метода лежит идея о замене целевой функции исходной задачи некоторой обобщенной функцией, значения которой совпадают со значениями исходной функции внутри допустимой области, а при приближении к границе области и при выходе из нее резко возрастают за счет другого слагаемого - штрафной функции. Метод штрафных функций может использоваться для исключения части или всех ограничивающих уравнений [2,стр.225]. Он сводит задачу на условный экстремум к решению задачи на безусловный экстремум, что часто приводит к упрощению вычислений. Особенно эффективно применяется этот метод в тех случаях, когда ограничения исходной задачи заданы нелинейными функциями.

Актуальной проблемой на данный момент  является разработка алгоритмов для решения нелинейных оптимизационных задач, позволяющих находить приближенное решение нелинейных оптимизационных задач с заданной                      по f(x) точностью:

                                                                  (2)

={1,2,…m} . 

В общем случае это означает бесконечный процесс минимизации вспомогательных функций для точного решения вспомогательных задач (1). Поэтому при решении задач математического программирования, часто возникает необходимость пользоваться эвристическими критериями остановки, не гарантирующими выполнения неравенства

,                                                               (3)

где   f* = min{f(x), xD(0)} ,                                       (4)

даже при включении итерационной точки xk  D(0). Здесь D(0) – замкнутое, выпуклое и ограниченное  множество, удовлетворяющее условию Слейтера. А ε- заданная точность нахождения f*,  {xk} - последовательность точек приближения.

В настоящей работе представлены разработанные алгоритмы для метода штрафов, допускающие приближенное решение вспомогательных задач с заданной точностью за конечное число итераций. Эти алгоритмы имеют легко проверяемые на практике критерии остановки, при выполнении условий которых гарантируется допустимость и заданная точность полученного решения. Выбор параметра p, в зависимости от заданной точности решения вспомогательных задач, обеспечивает требуемую точность решения задачи (4) [3, стр. 46].

Алгоритм 1 .

Задается требуемая точность решения ε > 0, x0  Rn, натуральное число N, число δ  (0,ε). Выбирается p из диапазона , возрастающая функция  φ(t) такая, что ,. Полагается k = 1.

1. Вычисляется Ck = φ(k).

2. Если k < N, то находится приближенное решение задачи  Переход к шагу 1 при k, измененном на k + 1.

3. Если k = N, то находится точка xN  A(), являющаяся                                  δ-оптимальным по функционалу решением задачи  Точка xN принимается в качестве ε - решения задачи (1).

Алгоритм 2 (модификация алгоритма 1).

Задается требуемая точность решения ε > 0, x0  Rn, натуральное число N, число   (0,ε). Выбирается , возрастающая функция φ(t) такая, что ,  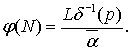      Полагается k = 1.

1. Вычисляется Ck = φ(k).

2. Если k < N, то находится приближенное решение задачи  Переход к шагу 1 при k, измененном на k + 1.

3. Если k = N, то находится точка xN  A(), являющаяся                           -оптимальным по функционалу решением задачи  Точка xN принимается в качестве ε - решения задачи (4).

Алгоритм 3.

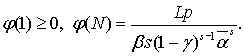Задается требуемая точность решения ε > 0, x0 Rn, числа δ  (0,ε), γ  (0,1), натуральное число N. Выбирается 0<p≤, возрастающая функция φ(t) такая, что  Функция штрафа выбирается вида  при s > 1.          Полагается k = 1.

1. Вычисляется Ck = φ(k).

2. Если k < N, то находится приближенное решение задачи  Переход к шагу 1 при k, измененном на k+1.

3. Если k = N, то находится точка xn  A(), являющаяся δ-оптимальным по функционалу решением задачи min Fγ(x, CN). Точка xN принимается в качестве ε - решения задачи (1).

Алгоритм 4 (модификация 3-го алгоритма).

Задается требуемая точность решения ε > 0,  x0 Rn, числа   (0,ε),  γ(0,1), натуральное число N. Выбирается  0 < p ≤ возрастающая функция φ(t) такая, что  . Функция штрафа выбирается вида: при s>1(в данном случае s=2). Полагается k = 1.

1. Вычисляется Ck = φ(k).

2. Если k < N, то находится приближенное решение задачи  Переход к шагу 1 при k, измененном на k+1.

3. Если k = N, то находится точка xn  A(), являющаяся                              -оптимальным по функционалу решением задачи min Fγ(x, CN). Точка xN принимается в качестве ε - решения задачи (4).

Алгоритм 5 .

Задается требуемая точность решения ε > 0, x0  Rn, натуральное число N, число δ  (0,ε). Выбирается, возрастающая функция  φ(t) такая, что , . Полагается k = 1.

1. Вычисляется Ck = φ(k).

2. Если k < N, то находится приближенное решение задачи  Переход к шагу 1 при k, измененном на k + 1.

3. Если k = N, то находится точка xN  A(), являющаяся δ-оптимальным по функционалу решением задачи  Точка xN принимается в качестве ε - решения задачи (1).

Алгоритм 6 (частный случай алгоритма 5)

Задается требуемая точность решения ε > 0, x0  Rn, натуральное число N, число δ  (0,ε). Выбирается  ,  возрастающая функция  φ(t) такая, что , . Полагается k = 1. Выбирается функция штрафа вида .

1. Вычисляется Ck = φ(k).

2. Если k < N, то находится приближенное решение задачи  Переход к шагу 1 при k, измененном на k+1.

3. Если k = N, то находится точка xN  A(), являющаяся δ-оптимальным по функционалу решением задачи  Точка xN принимается в качестве ε - решения задачи (1).

Если используется штрафная функция вида , то можно выбирать ,  и  Здесь p – такое число p =p(ε), p > 0, что из включения x(C)  D(0) будет следовать неравенство | f(x(C)) - f* |  ≤ ε. L-константа Липшица для функций f(x) на G, L>0, где |f(x)-f(y)|<L||x-y||,x,yGиGRn;    β, γ – параметры аппроксимации, где γ [0,1) и β>0 ;

δ-1(p) – функция, обратная к модулю выпуклости δ(t) и 0<p<;

Ck -коэффициент штрафа вычисляемый по правилу Ck=a*k, где а – параметр, используемый для вычисления коэффициентов штрафа. Множество  - аппроксимация допустимого множества; g(x) – функция равномерно выпуклая на множестве D(0) c неубывающим модулем выпуклости δ(t), где δ(t) - функция, определенная при всех t, где ()  при всех х, у G, где G - выпуклое множество и G Rn (f(x) - определенна на этом множестве). Точка ; - число, причем ; - число, , где ;  - функция штрафа; k- номер итерации; δ - число, δ  (0,ε).

Для программной реализации представленных алгоритмов было использовано разработанное авторами в среде Borland Delphi 7.0 приложение [4]. В ходе проведенного анализа по решению 50 тестовых задач  выпуклого программирования представленными алгоритмами было выяснено, что первый, третий и шестой алгоритмы обладают следующими свойствами:

·     позволяют решать оптимизационные задачи за меньшее число итераций;

·      трудоемкость вычисления наименьшая;

·     вероятность достоверности  результата более высока, по сравнению с другими алгоритмами;

·     точность решения зависит от оцениваемого параметра p, который используется в промежуточных вычислениях;

·     требуется меньшее количество времени на решение задач.

Для второго, четвертого, пятого алгоритмов  характерными чертами являются:

·        высокая трудоемкость вычисления и большое число итераций;

·        точность решения зависит от оцениваемого параметра p, который используется в промежуточных вычислениях;

·        для некоторых задач решение находится за одинаковое число итераций для всех трех алгоритмов;

·        требуется большее количество времени на решение задач.

По результатам работы приложения можно также сделать вывод, что параметр γ не сильно влияет на трудоемкость вычислений вспомогательной функции и  градиента, но его значение лучше брать из промежутка [0.5; 0.9].

Все рассмотренные алгоритмы вполне приемлемы и эффективны для решения различного рода задач выпуклого программирования.

 

 

Список использованной литературы:

 

1. Грешилов А.А. Прикладные задачи математического программирования: Учебное пособие. – 2-е изд. – М.: Логос, 2006. – 288 с.

2. Аоки М. Введение в методы оптимизации. М.: Наука. -1977. 343с.

3. Заботин Я.И., Фукин И.А. Алгоритмы в методе штрафов с аппроксимацией допустимого множества // Известия высших учебных заведений.Математика. – 2004. – №1.- С.36-47.

4. Исавнин А.Г., Хамидуллин М.Р. Программная реализация решения задач выпуклого программирования алгоритмами метода штрафных функций с неполной минимизацией вспомогательных функций // Электронное научное периодическое издание  (Интернет-журнал) «Образование и наука Закамья Татарстана», - №18 (сентябрь), - 2010.       Режим доступа: http://www.nauctat.ru