*99707*

ФИЗИКА/ 2.Физика твердого тела.

Захарченко Р.В.1,2, Захарченко В.Н.1

1Національний технічний університет України «КПІ», Україна

2Лабораторія дослідження матеріалів при Національному політехнічному інституті Мексики, відділення Керетаро, Мексика

Квантово-механічне трактування природи кольору склоподібних SiO2 та SiO2 − ПММА матеріалів, легованих органічними барвниками

         Вступ. Різноманітні квантові замкнені системи займають провідну роль в сучасній фізиці напівпровідників та технології, тому їх адекватне описання має велике теоретичне та практичне значення. Окрім цього ефекти квантової герметизації також проявляються в наноструктурних органічно модифікованих композитних матеріалах (див. наприклад [1, 2-7]), в яких набір енергетичних рівнів електронів, делокалізованих в межах молекули органічного барвника, визначає колір матеріалів, що використовують в лазерах та в декоративних цілях. Точна квантово-механічна трактовка проблеми “частинка в ящику” має дуже важливий елемент – граничні умови, які фактично визначають власні функції та власні значення відповідного рівняння Шредінгера. Для пояснення природи кольору використовували наближення FEMO (free electron molecular orbitals) моделі [8-10], вважаючи електрон делокалізованим в межах молекули, яка трактується як двовимірна потенціальна яма. В цьому класичному наближенні використовується умова непроникних стінок, яка передбачає рівність нулю хвильової функції на границях квантової системи; також наближення дає гарне описання енергетичного спектру без будь-яких регульованих параметрів. З іншого боку, також є очевидним, що ці умови не є реалістичними, бо вони не враховують характер взаємодії частинки (електрона) з границею. З розвитком скануючої електронної мікроскопії стало очевидним, що ця взаємодія найчастіше може бути представлена як відбиття, що, в свою чергу, веде до чіткої моделі стоячих хвиль, сформованих інтерференцією падаючої та відбитої хвиль, які можна спостерігати за допомогою вищезгаданого метода [11, 12]. Дзеркальне відбиття електронів від поверхні також використовувалось як один з частинних випадків проблем поверхневого електронного розсіювання в фізиці напівпровідників [13].

         Наступний параграф є спробою ввести граничні умови “дзеркального відбивання” в квантово-механічну трактовку частинки, замкненої в двовимірних квантових ямах різної геометрії, та порівняти отримані результати із знайденими за допомогою традиційних граничних умов.

         Теоретичний розгляд. Двовимірні наносистеми. Стаціонарне рівняння Шредінгера для частинки (електрона) в квантовій ямі з нульовою потенціальною енергією всередині останньої, має вигляд

де,  - це енергія частинки, – її маса; хвильова функція Ψ є функцією x, y в двовимірному випадку та функцією x, y, z в тривимірному випадку. Відповідно, квадрат хвильового вектора у першому випадку буде , а в другому . Далі ми обсудимо розв’язки цього рівняння для декількох частинних випадків.

А. Прямокутник. Вважатимемо, що частинки замкнені в межах прямокутної ями із сторонами a та b, орієнтованими вздовж осей “x” та ”y” як зображено на Рис. 1. Ефект замикання забезпечується “стінками” і розв’язок задачі визначається граничними умовами, що накладаються на систему; потенціальна енергія всередині прямокутника не впливає на розв’язок, оскільки вона стала за значенням (у нашому випадку вона дорівнює нулю). Рівняння Шредінгера для даної системи просто розв’язується за допомогою методу розділення змінних, який дає розв’язок у формі

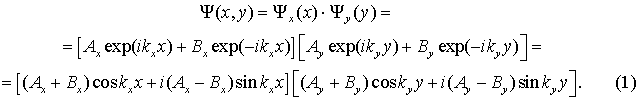
Оскільки рівняння Шредінгера в нашому випадку не змінюється з інверсією координат, його власні функції можуть бути або парними або непарними, а саме:

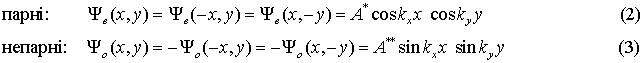
Для визначення можливих значень хвильового вектора необхідно застосувати граничні умови. Традиційні граничні умови непроникних стінок передбачають, що  при  та при . Вони дають

Очевидно, хвильова функція набуває непарної форми (3) з відповідними значеннями kx,y і енергетичний спектр частинки в прямокутнику буде

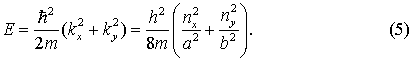
де “m” це маса частинки, а nx,y – квантові числа.

         Значно менш специфічними є періодичні (Борна-Кармана) граничні умови, що часто використовуються в теорії твердого тіла, які передбачають можливість частинки покинути потенціальну яму (тобто стінки проникні), але після проникнення частинки крізь стінку вона миттєво потрапляє в одну з еквівалентних, приєднаних до початкової ями з кожної сторони, ям (такі ями зображені на Рис. 1 пунктирними лініями). Дане припущення стверджує, що коли одна частинка покидає яму з однієї сторони, інша еквівалентна частинка входить в неї з іншої сторони, що часто, як випадок, наводять у якості приклада при розгляданні проблем, пов’язаних із переносом електричного струму. Інший приклад це дійсна сукупність еквівалентних ям із періодичною структурою, подібно до сукупностей молекул органічного барвника, що досить часто зустрічається на практиці. Застосувавши ці умови до (1) можна побачити, що у власних функціях з’являються  множники; прирівнюючи їх до 1, ми отримаємо , і, таким чином, енергія буде

з енергетичним спектром того ж типу, що і в (5), але з відмінним в 4 рази масштабом. Обидва типи хвильової функції (парна та непарна (2, 3)) можуть існувати, що просто довести аналізуючи умову .

         Тепер ми введемо інший тип граничних умов: ми приймаємо, що взаємодія частинки із стінкою має характер дзеркального відбивання (подібні умови інколи вводяться при розгляді проблем пов’язаних із поверхневим розсіянням носіїв заряду [11-14]). Нескладно побачити, що якщо ми вважаємо стінки потенціальної ями подібними до дзеркала, то це дійсно нам дає квазі-періодичну структуру, сформовану початковою ямою та її багаторазовими відбиваннями, як показано на Рис. 1; це також передбачає, що будь-яка вибрана точка в межах ями (хрест з координатами х, у  на Рис. 1) є еквівалентною до її відбивань, зображених на рисунку точками, таким чином

 

         Застосувавши ці умови до (1) ми вводимо множники , що дає для значень “k”, прирівняних до 1, наступні рівняння , які еквівалентні до (4) і приводять до енергетичного спектру (5). Той же результат можна отримати застосувавши ці умови до хвильової функції у формі (2). Таким чином, ми бачимо, що застосування таких граничних умов “дзеркального відбивання” у нашому випадку еквівалентне до періодичних умов, але із подвійним періодом по відношенню до початкового розміру ями (якщо ми подвоїмо розміри ями a, b в (6), то отримаємо спектр (5)); вищезгадані умови передбачають, що хвильова функція парна, і має знайдені значення хвильових чисел k.

         На жаль, слід зазначити, що енергетичний спектр (5) в дійсності описує дві незалежні системи (в напрямках “x” та ”y”) стоячих хвиль де-Бройля, сформованих відбиванням хвиль від протилежних стінок потенціальної ями, і умови (4) означають, що при кожній довжині a, b парні номери відповідних напівдовжин хвиль можуть мати місце (довжини хвиль ); таким чином, умови дзеркальних стінок приводять нас до однозначного розуміння отриманого раніше спектру. І, як очевидний частинний випадок щойно дослідженої проблеми, ми можемо привести у якості приклада одновимірну яму (з розміром а) з дзеркальними стінками: відповідні стоячі хвилі системи підкорюються умові . Це дає для хвильового вектора співвідношення , що подібне до (4), і для енергетичного спектру маємо

Б. Прямокутний трикутник з двома однаковими сторонами. Нехай трикутник має дві сторони довжиною а, як зображено на Рис. 2; 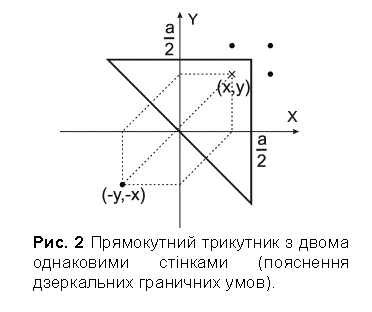довільна точка з координатами х, у зображена хрестом, а крапками зображені відбиття цієї точки, як результат накладання граничних умов типу стінки-дзеркала (квазі-періодична структура, подібна до розглянутої на Рис. 1, для цього випадку також може бути сконструйована, але тут вона не представлена). Загальний розв’язок рівняння Шредінгера знову (2, 3). Умови, що накладаються на власні функції дзеркальними стінками можна записати таким чином:

Застосовуючи першу з них до парної чи непарної функцій, ми отримуємо для обох випадків, що . Використання інших двох умов дає для парної Ψ-функції (2)

для n – будь-якого цілого числа починаючи з 1. У випадку непарної функції (3) ми отримуємо

де n може бути будь-яким цілим числом починаючи з 0. Таким чином, для непарних розв’язків отримуємо набір енергетичних рівнів

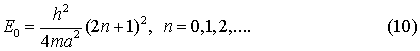
І для парних розв’язків, в свою чергу, маємо

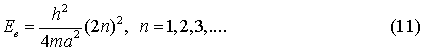
Слід зазначити, що якщо у виразі (10) вміщуються всі непарні цілі числа у якості квантових чисел, а формула (11) вміщує, відповідно, лише всі парні числа, то загальний набір енергетичних рівнів для такого прямокутного трикутника з однаковими сторонами буде даватись виразом

де n – будь-яке ціле число починаючи з одного. Трансляційна симетрія квазі-періодичної структури застосована для цього випадку (період 2а в обох напрямках) приводить точнісінько до виразу (12) для енергії.

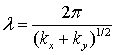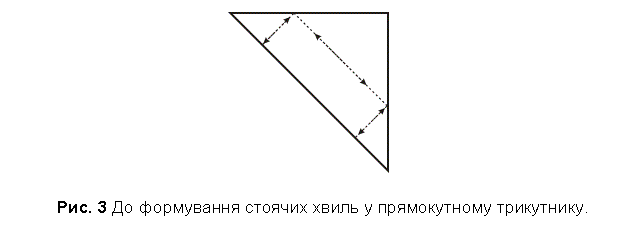
         Розрахунок системи відповідної стоячої хвилі дає для довжини хвилі  співвідношення  для “непарного” випадку, та  у випадку “парному”, що виглядає правдоподібним якщо ми приймемо до уваги, що величина  є довжиною шляху, пройденого стоячою хвилею, як зображено на Рис. 3 пунктирною лінією всередині початкового трикутника, як один з можливих випадків створити стоячу хвилю.

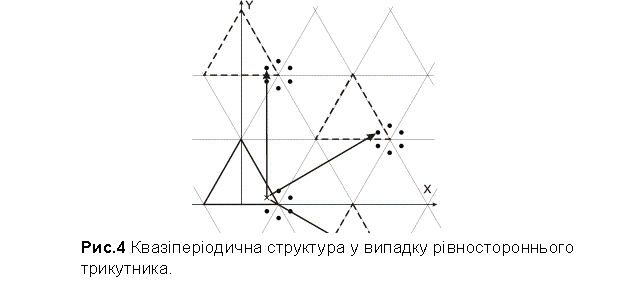
В. Рівносторонній трикутник. На Рис. 4 зображений трикутник, у якого кожна із сторін дорівнює а, і який розміщений в прямокутній декартовій системі координат так, що його нижня сторона прямує вздовж осі “x”, у той час як вісь “y” є його віссю симетрії. Загальний розв’язок рівняння Шредінгера шукаємо знову ж таки у формі (2, 3) і застосуємо “дзеркальні” (відбиваючі стінки) граничні умови. На Рис. 4 ми бачимо квазі-періодичну структуру, сформовану багаторазовими відбиваннями трикутника від його стінок; точка в середині початкових стінок (хрест) та її відбивання, зображені крапками, ясно демонструють характер періодичності цієї структури. Три стрілки представляють вектори трансляції даної структури. Можна побачити, що подібно тому, як і у випадку прямокутної ями, ці вектори трансляції мають подвійну довжину у порівнянні з розмірами початкової ями у відповідному напрямку (тобто ); ці напрямки формують кути  з віссю абсцис, і кут між сусідніми векторами складає , що погоджується із симетрією системи. Отже, отримані умови періодичності структури можна виразити у формі

Застосування цих умов до хвильової функції в будь-якій з вище згаданих форм (1, 2, 3) дає нам наступні вирази для хвильових векторів: a) може бути довільним (не квантований), б)

         В цих співвідношеннях n1,2,3 може бути будь-яким цілим числом починаючи з 1, а хвильові функції можуть бути як парними так і непарними. Для енергетичного спектру ми отримуємо два набори енергетичних рівнів:

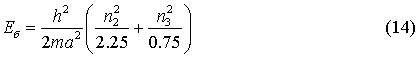
Як і у випадку прямокутної ями, ми можемо вивести характер стоячих хвиль де-Бройля з отриманих хвильових векторів. Умова (а) визначає хвилю, нормальну до двох сторін трикутника і відбиту під кутом  від його третьої сторони (двонаправлені пунктирні лінії на Рис. 5 показують один з прикладів; точка відбивання може бути різною, але це не впливає на довжину лінії. Її подвійна довжина 1,732а відповідає цілому числу довжин хвиль ). Перша частина умови (б) відповідає хвилі, що циклічно обертається всередині трикутника з відбиванням від усіх сторін з кутом падіння  (на  Рис. 5 однонаправлена пунктирна лінія /за годинниковою стрілкою/ з довжиною 1.5а рівною цілому числу довжин хвиль ); а друга частина умови (б) відноситься до попереднього типу хвиль, але в трикутнику напів-розміру, який можна спостерігати як результат хвильової дифракції в точці відбивання, з наступним відбиванням від іншої сторони.

         Енергетичний спектр досліджуваних матеріалів. Резюмуючи отримані в попередньому розділі результати зазначимо, що рівні енергії електронів у випадку прямокутної ями з розмірами  при застосуванні періодичних граничних умов Борна-Кармана (що виправдано наявністю агрегатів молекул) описуються виразом

де h – стала Планка, m – маса вільного електрона, та nx,y – квантові числа. В таблицях 1-4 (попередні тези «Склоподібні SiO2 та SiO2 − ПММА матеріали, леговані органічними барвниками») надано приклади порівняння розрахункових даних з експериментом. Вказані розміри є реальними, вони отримані сумуванням довжин індивідуальних зв’язків [15] з додаванням однієї довжини зв’язку з кожної сторони молекули, як це прийнято робити [8, 9].

         Беручи до уваги відсутність в (15) корелюючих параметрів, можна казати про гарне погодження розрахунку з експериментом; важливо також відзначити, що увесь спектр описується за допомогою набору найменших можливих значень квантових чисел (), таким чином, всі розраховані рівні енергії, що потрапляють у видиму область, погоджуються з експериментом.

         Для такої ж прямокутної потенційної ями з непроникними стінками (нульові граничні умови для Ψ-функції) електронні рівні енергії описуються виразом

в якому значення енергії в 4 рази відрізняються від попереднього випадку. Зрозуміло, що всі рівні, що даються (15), можна отримати з (16) при подвоєних значеннях квантових чисел.

          З табл. 3 (попередні тези «Склоподібні SiO2 та SiO2 − ПММА матеріали, леговані органічними барвниками») видно, що розрахунки для випадку родаміна задовільно погоджуються з експериментом.

         Застосувавши такий підхід до кармінової кислоти, можна визначити в її молекулярній структурі елементи, що створюють умови для утворення набору стоячих хвиль. До таких слід віднести практично прямокутну область з розмірами L1×L2, позначену на Рис.1 попередніх тез «Виготовлення гібридного покриття ПММА - SiO2 та його структурні особливості» суцільними лініями, та дві пунктирні прямі лінії АВ (L3) та CD (L4), які можна розглядати як структуроподібні ланцюжки. Ланцюжок атомів із стоячими хвилями де Бройля як застосування ідеї "відбиваючих стінок" до одновимірного випадку дає наступний набір рівнів енергії

(ціла кількість де бройлівських напівхвиль вкладається на довжині ланцюжка Li), індекс і нумерує ланцюжок, ni – ціле число, починаючи з 1. Для прямокутника використаємо вираз (16), для ланцюжків - (17). В табл. 4 порівнюються розрахункові та експериментальні дані і в цьому порівнянні спостерігається задовільне погодження розрахунків з експериментом.

         Вплив матриці в рамках нашого аналізу, який враховує реальну геометрію молекули, пов’язану з різним ступенем деформації в залежності від оточення молекули: малі зміни розмірів викликають відповідні зміни спектрального положення спостерігаємих полос. Зокрема, у випадку родаміна більш жорстка скляна матриця передбачає менші молекулярні розміри і, відповідно, більш високі енергії електронного переходу; в більш м’якій матриці ПММА розмір молекули трохи більший із відповідним впливом на спектр.

         Повертаючись до механізму деградації, можна пов’язати його зі зміною форми молекули. Найбільш детальні дослідження цього ефекту виконані для кармінової кислоти. Як вже згадувалось, з ІЧ-даних випливає, що відпалювання “роздягає” молекулу, залишаючи незайманим її ядро з бензольних кілець. Така зміна геометрії радикально змінює енергетичний спектр і, відповідно, спектр поглинання (зменшення “ширини” молекули зсуває спектр в ультрафіолетову область). Той факт, що відпалювання має дуже слабкий вплив на полоси поглинання при 4.32, 3.1 та 1.9 еВ, дозволяє припустити, що вищезгадана видозміна молекули не впливає на форму та розмір лінії CD – “довжину” молекули. Згідно з нашим аналізом, саме ця лінія визначає положення вищезгаданих полос поглинання.

         Висновки. Забарвлені покриття та об’ємні зразки матеріалу з високою та стабільною оптичною густиною можуть бути сполучені шляхом модифікації склоподібної золь-гель матриці або гібридної полімерної золь-гель матриці шляхом введення органічних барвників. Розроблені оригінальні прості, недорогі та ефективні підходи для різних барвників.

         Кожна із введених органічних молекул задає свій набір електронних рівнів енергії, який визначається в першу чергу її формою та розмірами. Цей енергетичний спектр може бути розрахований на базі узагальненого наближення FEMO, яке розглядає рух електронів, делокалізованих всередині молекули (потенційної ями) з відбиваючими стінками. Такий підхід можна застосовувати, зокрема, до квазілінійного атомного ланцюжка та до молекули трикутної форми.

         Вплив матриці на енергетичний спектр можна звести до деформації та “ефекту оболонки”, тобто він визначається характером взаємодії молекули барвника із матрицею. Деградація кольору є результатом реструктуризації молекули, викликаної деградаційними факторами, що також змінюють її геометрію; найбільша стабільність кольору відповідає наявності щільної замкненої “оболонки”, яка в золь-гель матеріалі, який зазвичай має суцільну систему взаємопов’язаних пор, може бути забезпечена особою обробкою.

Література:

1.     Colthup, N.B. and Daly, L.H., Introduction to Infrared and Raman Spectroscopy, Boston: Academic, 1990, pp. 511–530.

2.     D. Avnir, D. Levy, R. Reisfeld, The Nature of the Silica Cage as Reflected by Spectral Changes and Enhanced Photostability of Trapped Rhodamine 6G, J. Chem. Phys. 88 (1984), pp. 5956-5959.

3.     C. Whitehurst, D.J. Shaw, T.A. King, SPIE-Proc. (Sol-Gel Optics) 1328 (1990) 785

4.     K.T. Knobbe, B. Dunn, P.D. Fugua, F. Nishida, Laser Behavior and Photostability Characteristics of Organic Dye Doped Silicate Gel Materials, Appl. Opt., 29 (1990), pp. 2729-2733.

5.     C. Sanchez, M. In, Molecular Design of Alkoxide Precursor for the Synthesis of Hybrid Organic-Inorganic Gels, J. Non-Cryst. Solids 147/148 (1992), pp. 1-12.

6.     A.N. Murashkevich, V.G. Vashina, I.M. Zharskii, Synthesis of Active Porous Silica Gel Materials and Investigation of Their Properties, J. Sol-Gel Sci. and Techn. 20 (2001), pp. 7-12.

7.     Griffits, J., Color and Constitution of Organic Molecules, London: Academic, 1976, pp. 24–29.

8.     Birks, J.B., Photophysics of Aromatic Molecules, London:Interscience, 1970, pp. 1–26.

9.     J.N. Murray, The Theory of the Electronic Spectra of Organic Molecules. John Wile & Sons, Inc., New York, 1963.

10. A. Biedermann, O. Genser, W. Hebenstreit et al., Scanning Tunneling Spectroscopy of One-Dimensional Surface States on a Metal Surface, Phys. Rev. Lett., 76 (1996), pp. 4179-4182.

11. M. Schmid, S. Crampin, P. Varga, STM and STS of Bulk Electron Scattering by Subsurface Objects, J. Electron Spectr. And Rel. Phenomena, 109 (2000), pp. 71-84.

12. W. Mönch, Semiconductor Surfaces and Interfaces, Springer-Verlag, Berlin Heidelberg, 1993.

13. S. Crampin, Surface States as Probe for Buried Impurities, J. Phys. Condens. Matter. 6 (1994), pp. L613-L618.

14. CRC Handbook of Chemistry and Physics, Weastle, R.C. and Astle, M.J., Eds., Boca Raton: CRC, 1979, pp. F216–F219.

15. A.G. Cullis, L.T.Canham, P.D.J.Calcott, J.Appl.Phys., 82 (1997), 909-963