*99579*

Махамбаева И.У., соискатель

КГУ им. Коркыт Ата

особенности решения задач геомеханики с учетом влияния выработок

Аннотация: Сформулированы граничные условия и некоторые особенности решения задач геомеханики с учетом влияния выработок

Сложность конкретных задач горного производства и современных теоретических методов приводит к необходимости использования численных методов и ПК. Еще недавно считалось, что процессы происходящие в массиве горных пород при проведении выработок случайны, и проектирование выработок осуществлялось на основе интуиции исполнителя и опыта прошлого строительства. Успехи геомеханики и вычислительной техники изменили представление о проектировании открытых и подземных горных выработок. Появление качественно новой электронно- вычислительной техники с большими быстродействиями и объемами памяти привели к интенсивному развитию и применению численных методов к решению практических задач геомеханики. Одними из передовыми и широко распространенными численными методами решения нелинейных задач геомеханики являются метод конечных элементов, а также последнее время интенсивно развивающийся метод граничных элементов.

Метод конечных элементов (МКЭ) является одним из самых распространенных методов решения прикладных задач. Наглядность метода, сравнительная простота его применения в случае областей сложного рельефа, а также возможность учета разнообразные и сложные свойства горных пород и грунтов сделали его весьма популярным среди широкого круга исследователей. В настоящее время МКЭ является мощным средством приближенного решения дифференциальных уравнений, описывающих различные физические процессы. МКЭ является универсальным, достаточно простым и доступным средством решения сложных разнообразных задач геомеханики. Он позволяет легко учитывать произвольно задаваемые граничные условия - в виде заданных контурных или массовых сил, заданных перемещений границ или внутренних точек области. С одинаковой простотой решаются задачи в однородных и неоднородных средах, в односвязных или многосвязных областях. Легкость МКЭ в установлении для различных областей исследуемого массива своих законов, функций связывающих узловые силы и перемещения дает возможность использовать различные элементы и значительно повышать эффективность метода.

В работе [1] разработаны геомеханические модели породного массива, отражающие полный комплекс прочностных и деформационных свойств горных пород. Эти модели в условиях плоской деформации реализованы на ЭВМ в виде численных процедур, обеспечивающих выполнение заданных законов состояния с помощью метода конечных элементов. Рассматривается двумерная область R, ограниченная контуром С (рис.1). В области R на контуре С в виде граничных условий задается только часть параметров (напряжения или смещения, иногда их комбинация), а остальные параметры отыскиваются в ходе решения задачи. Например, если на границе заданы смещения, то напряжения на границе (как и напряжения и смещения в любой точке области R) можно найти как часть решения задачи и наоборот. Если на границе С задано достаточно условий, то решения задачи определяются этими условиями единственным образом.

В методе конечных элементов вся область R разбивается на сетку элементов (рис.1), т. е. строится КЭ- модель области. Если в области R имеются оси симметрии A’- A’, то при решении задачи рассматривается только часть области относительно симметрии. На границах области С, когда не учитываются тектонические напряжения, ставятся следующие условия [2]:

- на верхней s_у=gН, t_ху=0;

- на нижней t_ху=0, u=0; (1)

- на боковых t_ху=0, u=0;

где Н- глубина от дневной поверхности, g- объемный вес.

При учете тектонических напряжений, на боковых границах имеем:

s_х= s_хр + s_хт , u=0, (2)

где s_хр =m s_у , s_хт = tgh- горизонтальные компоненты поля напряжений гравитации и тектоники; m= n/ (1- n)- коэффициент бокового распора; t- коэффициент тектоники.

Вектор узловых сил формируется из реально заданных сосредоточенных нагрузок или сведенных к узловым силам распределенных по контуру или по площади области сил. Силы тяжести приводятся к узловым силам путем умножения объемного веса на площадь элемента и распределяется поровну между тремя узлами. Если к свободному узлу не приложено никакой реальной внешней силы, то значит сумма сил от окружающих элементов в этом узле равна нулю. Если постановка задачи такова, что в каком- то из узлов (или в группе узлов) задано перемещение по одному (или обоим) координатному направлению, например u_i, то столбец матрицы жесткости системы ( МЖС ) с номером (2i- 1) следует умножить на заданную величину u_i и почленно перенести в правую часть уравнения, добавив к заданным узловым силам. Количество неизвестных сокращается, строка МЖС с номером ( 2i- 1) превращается в линейную комбинацию остальных строк и может быть удалена.

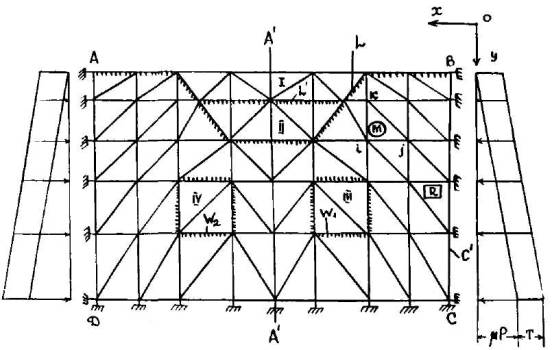
Рисунок 1. Общая расчетная схема: R - полная область; С - контур R; L - окончательный контур откоса; Wi, W₂ - контуры камер;

Система связей (заданных перемещений) должна быть такова, чтобы исключалось свободное перемещение или вращение области в поле координат. Минимальное число связей, обеспечивающих это условие- две по одной оси и одна по другой. При решении геомеханических задач в ряде случаев необходимо провести серию решений с последовательно изменяемыми контурами области, например при послойной выемке котлована, по этапной проходке тоннеля, подработки борта карьера камерами и др. В этих случаях вся серия решений может быть приведена по одной сети КЭ- модели в автоматическом режиме с помощью следующей процедуры.

В области (R ) необходимо образовать откос с окончательным контуром (L ), затем подработать его камерами с контурами W1 и W2 . Удаление той или иной группы элементов достигается путем присвоения им модуля упругости Е =0 и объемного веса g = 0 при одновременной фиксации узлов окруженных только нулевыми Е. Элементам последовательно вынимаемых слоев присваиваются номера типов, равные номеру этапа выемки I,II,III,IV и др. (рис.1), а всем этим типам присваиваются реальные характеристики пород. Организуется цикл по числу этапов выемки. В каждом цикле: 1) всем элементам, номер типа которых совпадает с номером цикла, присваивается номер типа I; 2) просматриваются все узлы области, а в каждом цикле по узлам все элементы. Если узел окружен только элементом первого типа, то узлы присваиваются признаки фиксации по всем координатным направлениям; 3) для всех элементов области, имеющих тип I (т.е. извлекаемых в данном этапе выемки), вычисляются узловые силы по напряжениям, предшествующим выемки данного слоя. Из вычисленных узловых сил (с обратным знаком) формируется вектор нагрузки системы.

После выполнения всех перечисленных операций из области будет удалена очередная II группа элементов, а к вновь образованному участку контура будут приложены силы, эквивалентные напряжениям снимаемым с контура при удалении слоя. Силы, вычисляемые и прикладываемые к внутренним узлам удаленной зоны, никакого участия в дальнейших решениях принимать не будут, так как этим узлам присвоены признаки фиксации, и при решении системы соответствующие уравнения игнорируются. Таким образом, после удаления I – II групп элементов в массиве образуется откос контуром L. После этого последовательное удаление элементов III и IV группы позволять образовать камеры с контурами W₁ и W₂. Отметим, что процедура может быть выполнена, по желанию, различными вариантами образования выработок. Для этого остается только поменять нумерации этапов выемки.

Первоначально задача решается для рассматриваемой полной области ABCD. Находим тензор напряжений s^о_{i j} и деформаций e^о_{i j} , перемещение u^о_{i j}. Запоминаем их в памяти ЭВМ, если надо – печатаем. В зависимости от заданного закона состояния, а также граничных условий (1), (2) (приложение на границу внешних сил и перемещений) найденные значения могут быть упругими или же упруго – пластическими, соответствующими какому-то циклу итераций. Формирование откоса и камер будем имитировать серией шагов изменения контуров области. В первом шаге решения внимаем первый слой I на глубине Н¹. Элементам первого слоя задаем величины Е = 0, g = 0. Фиксируем жестко те узлы, которые окружают элементы только с нулевым модулем упругости. При этом элементы первого слоя заменяются пустыми элементами, которые не нарушают основной сети КЭ – модели. Удаление элементов слоя I приводит к тому, что часть контура L освобождается от давления (усилия) вышележащей толщи:

F^/ = F^/(s^o_x , s^o_y , t^o_{x y}) (3)

Освобождение L^/ от усилий означает, что к контуру L^/ нужно приложить распределенные нагрузки, противоположные (с обратным знаком) усилиям из (3). Далее решается задача с заданными новыми граничными условиями и контурами L^/C для невесомой среды. Найденное приращение напряжений, деформаций и смещений прибавляется к предыдущим решениям для полной области:

s¹_{i j} = s^o_{i j} + Ds¹_{i j} ,

e¹_{i j} = e^o_{i j} + De¹_{i j} , (4)

u¹_{i j} = u^o_{i j} + Du¹_{i j} .

Если же суммарное значение напряжений и деформаций удовлетворяет закону состояния, то (4) будет окончательным. Если же нет, продолжаем итерации до достижения заданной точности и находим окончательное решение:

s¹_{i j 0} = s¹_{i j} + Ds _{i j} ,

e¹_{i j 0} = e¹_{i j} + De _{i j} , (5)

u¹_{i j 0} = u¹_{i j} + Du _{i j} ,

Во втором шаге вынимаем II слой, определим снимаемую нагрузки для L: F^II = F^II(s¹_x , s¹_y , t¹_{x y}). Повторяем все выше сказанное и получим решение для второго шага s²_{i j 0}, e²_{i j 0}, u²_{i j 0} и т.д.

Решение задачи в K-том шаге имеет следующий вид. Находим нагрузки F^K = F^K(s_x^K-1 , s_y^K-1 , t_xy^K-1) при выемке K-го слоя. После первой итерации имеем:

s^K_{i j} = s^K-1_{i j} + Ds^K_{i j} ,

e^K_{i j} = e^K-1_{i j} + De^K_{i j} , (6)

u^K_{i j} = u^K-1_{i j} + Du^K_{i j} .

Если (6) удовлетворяет закону состояния, то является окончательным решением задачи при образовании выработок, если же нет, тогда делаем последующих итераций до удовлетворения заданной точности и получим окончательное решение

s^K_{i j 0} = s^K_{i j} + Ds _{i j} ,

e^K_{i j 0} = e^K_{i j} + De _{i j} , (7)

u^K_{i j 0} = u^K_{i j} + Du _{i j} .

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Абдылдаев Э.К. Напряженно-деформированное состояние массива горных пород вблизи выработок. - Фрунзе : Илим, 1990.-с.164

2. Абдылдаев Э.К. Метод конечных элементов при решении прикладных задач. – Алматы.: Полиграфия-сервис, 2011, - 111 с.