Современные информационные технологии/1. Компьютерная инженерия

д.т.н., профессор Лукашенко В.М., к.т.н. Лукашенко А.Г.,
к.т.н. Уткина Т.Ю., аспирант Лукашенко Д.А., магистр Лукашенко В.А.

Черкасский государственный технологический университет, Украина

МЕТОДИКА ОПТИМИЗАЦИИ ПАРАМЕТРОВ
КОМПОНЕНТОВ МИКРОПРОЦЕССОРНЫХ СИСТЕМ

При проектировании функциональных преобразователей, реализуемых таблично-алгоритмическим методом с введением кортежной корректировки входной независимой переменной, теоретический, практический интерес представляет метод определения оптимального числа групп, положенный в основу методики проектирования.

Известно [1-3], что основные требования к специализированным цифровым функциональным преобразователям, используемых в аэронавигации, являются:

- малые аппаратурные затраты;

- высокое быстродействие;

- требуемая высокая точность;

- высокая надежность;

- малые габариты, вес и т.д.

Одновременное выполнение всех перечисленных требований является задачей трудоемкой и в ряде случаев (при большом ) невыполнимой. Поэтому поиск оптимального варианта из всего выше перечисленного является задачей актуальной.

Целью работы является разработка методики оптимизации параметров компонентов микропроцессорных систем при таблично-алгоритмической аппаратурной реализации.

Решение проблемной задачи

В зависимости от числа групп при заданной разрядности  можно варьировать аппаратурными затратами, быстродействием. Кроме того, известно [4-5], что малые аппаратурные затраты обеспечивают не только малую стоимость, но и малое энергопотребление (мало число элементов), что в свою очередь уменьшает габариты, вес, и следовательно, увеличивает время безотказной работы, уменьшает интенсивность отказов [6]. Определение оптимального числа групп выполняется в следующей последовательности:

- определяется зависимость аппаратурных затрат для заданного  от числа групп, на которые разбиваются коды функции и аргумента;

- строится график этой зависимости;

- определяется зависимость быстродействия устройства преобразования от числа групп;

- строится график этой зависимости;

- совмещаются абсциссы этих графиков;

- определяется абсцисса точки пересечения двух функций, ближайшее целое число является оптимальным по быстродействию и аппаратурным затратам.

Естественно, что при разработке проекта вычислительного устройства необходимо стремится к достижению наилучших значений всех параметров. Однако в общем случае важность и значимость этих параметров различна. Один из параметров может быть определяющим для высокого качества всего вычислительного комплекса в целом. При этом, достижение других высоких параметров может быть менее существенным [5-6].

В таком случае задача определения числа групп сводится к отысканию:

1. Точки пересечения функциональной зависимости соответствующего параметра от числа групп () и прямой, независимой от , ордината которой задана техническими требованиями этого параметра.

2. Абсциссы этой точки.

3. Ближайшее большее целое значение абсциссы присваивается числу групп.

Если определяющих параметров будет несколько, то могут возникнуть варианты:

- целое число групп равно  по одному из параметров;

- целое число групп равно  по другому параметру.

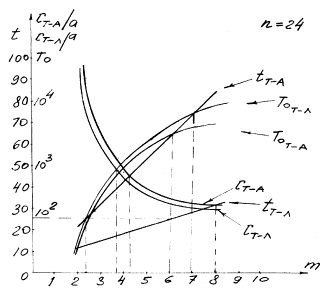
Рисунок 1 – Графики зависимостей , , от числа подматриц 

Учитывая, что от  зависят и другие основные параметры устройства, то необходимо для полученных  и  по аналитическим выражениям рассчитать все параметры и выбрать наиболее приемлемые.

Например, на графике показано определение числа групп для двух способов реализации функциональных преобразователей с разрядностью аргумента и функции , таблично-аддитивного (Т-А) и таблично-логического (Т-Л) методов. Характеристикой быстродействия устройства является время, необходимое для выработки результата с заданной методической погрешностью, выраженное через число задержки на операцию выборки .

Аналитические выражения  для этих функциональных преобразователей имеют вид:

где  – время задержки при прохождении через блок вентилей В1;

 – время задержки при прохождении через блок вентилей В2;

 – время задержки при прохождении через блок вентилей В3;

 – время задержки при прохождении через комбинационную схему;

 – время задержки при прохождении через коммутатор;

 – время задержки при считывании констант из числового блока ПЗУ;

 – время сложения одной группы;

 – время переброса триггера из одного состояния в другое;

 – время задержки при прохождении через блок распределительный БР;

 – время задержки при дешифрации.

Математические модели аппаратурных затрат  для таблично-аддитивного и таблично-логического метода имеют вид соответственно:

где  – стоимость одного разряда регистра;

 – стоимость одного разряда цепей выдачи кода;

 – стоимость цепи выдачи одного адреса;

 – стоимость одного разряда цепей сумматора;

 – стоимость одного бита числового блока памяти;

 – стоимость одного логического элемента.

Кроме того, для иллюстрации метода приведена зависимость среднего времени наработки на отказ , аналитическое выражение которой определяет характеристику надежности и имеет вид:

где  – интенсивность отказа одного элемента,  [1/ч.];

 – число элементов в устройстве.

Из графика (рис. 1) видно, что оптимальным числом групп для  является . Если определяющим является , то следует выбрать таблично-логический метод, при этом .

Данная методика определения оптимального числа групп распространяется и на устройства умножения двоичных чисел.

Выводы:

Разработана методика определения оптимального числа групп, на которые разбиваются информационные коды операционных устройств. Она является общей и для функциональных преобразователей, и для таблично-алгоритмического устройства умножения и позволяет использовать ее при различной значимости параметром компонентов микропроцессорных систем.

Литература:

1. Корпань Я. В. Алгоритм подготовки массива данных для автоматизированных технологических процессов / Я. В. Корпань, А. Г. Лукашенко, В. М. Лукашенко // Прогрессивные направления развития машино-приборостроительных отраслей и транспорта : Тр. науч.-техн. конф., 2004 г. – Севастополь : СевНТУ, 2004. – Т. 2. – С. 71–72.

2. Лукашенко В. М. Высокоскоростной функционально ориентированный преобразователь / В. М. Лукашенко // Вісник ЧІТІ. – 1999. – № 1. – С. 19–21.

3. Аналіз технічних параметрів у інформаційних системах на основі теорії подібності та розмірності / В.М. Лукашенко, Я. В. Корпань, А. Г. Лукашенко и др. // Зб. наук. праць Кіровоградського національного технічного університету. – Кіровоград : КНТУ, 2007. – Вип. 19. – С. 201–204.

4. Лукашенко А. Г. Виявлення резерву предмета дослідження на основі теорії неповної подібності та розмірностей / А. Г. Лукашенко, О. А. Кулигін, В. М. Лукашенко. – Хмельницький : Вісник ХНУ. – 2009. – № 3. – С. 184–187.

5. Лукашенко А. Г. Эффективный метод анализа сложных моделей и их компонентов для специализированного лазерного технологического комплекса / А. Г. Лукашенко, Д. А. Лукашенко, В. М. Лукашенко и др. // Вісник ЧДТУ. – 2011. – № 4. – С. 42–47.