Современные информационные технологии/1.Компьютерная инженерия

К.т.н. Ткаченко В.Г., аспирант Клещёв А.О.

Одесская национальная академия связи

Проверка связности и цикличности фрагмента сети на основе

монотонных булевых функций

Широко известен метод проверки связности и цикличности на основе поиска в глубину [1], для проверки связности также применяют формирование матрицы достижимости по матрице смежности [2]. Реализация поиска в глубину предполагает прохождение всех еще не пройденных вершин вглубь, пока это возможно. Метод построения матрицы достижимости предполагает объединение строк матрицы смежности, которые относятся к вершинам смежным с вершинами уже найденными на предыдущем этапе.

Однако в методе поиска в глубину используется матрица инцидентности, за счет этого осложнены битовые операции и для хранения обязателен двухмерный массив. Также сам метод поиска в глубину чаще всего реализуется рекурсией, что подразумевает выделение большого количества памяти из стека и динамическое выделение памяти для хранения значений. В случае с методом формирования матрицы достижимости, для каждого нового подграфа необходимо формировать новую матрицу смежности, также затруднены проверки цикличности.

Для решения подобных задач, определения наличия циклов и связности предлагается следующий алгоритм.

1. Происходит пробег по всем ребрам в транспонированной матрице инцидентности, до тех пор, пока не будет найдено первое ребро, входящее в выбранный подграф согласно выборке из ребер. Первый найденный элемент сохраняется отдельно, в дальнейшем сохраненное значение будет являться маской использования вершин графа, для простоты - маска.

2. Согласно выборке из ребер выписываются все номера ребер в отдельный массив, кроме номера ребра, вершины которого были сохраненного в маску. Число ребер в массиве записывает отдельным числом – счетчиком массива.

3. Поочередно происходит операция И выбранных элементов матрицы по номерам из сохраненного массива с текущей маской. Если результат отличен от нуля, значит одна или более вершин ребра уже находится в маске и можно переходить к следующему шагу. Если результат равен значению элемента матрицы - исследуемый подграф содержит цикл и не является остовом (обе вершины ребра уже есть в маске), алгоритм завершает работу, так как подграф не является остовом или деревом. Если весь массив пройден, но не было значения отличного от 0, алгоритм завершает работу по причине отсутствия связности с некоторыми вершинами – подграф не является деревом или остовом.

4. К маске присваивается результат операции ИЛИ над маской и ребром из матрицы инцидентности (в маске появляется новая вершина), номер ребра в массиве номеров ребер замещается на последний элемент согласно счетчику элементов массива, счетчик элементов массива уменьшается на 1.

5. Если счетчик элементов массива указывает, что в массиве еще остались элементы, происходит возврат к этапу 3, начиная с первого элемента массива. Если счетчик достигнет значения 0 – алгоритм завершает работу, подграф является деревом, если число выбранных ребер соответствовало числу вершин минус один, то подграф является остовом.

Для представления графа используется транспонированная матрица инцидентности, что сильно упрощает поиск циклов и проверку связности. В методе используется только одна матрица без создания видоизмененных копий и копий для рекурсии, за счет чего происходит экономия памяти. За счет использования только простой арифметику и булевых функций [3], может быть реализован на любых микроконтроллерах и процессорах. Из недостатков следует отметить, что использование направленного графа невозможно.

Поскольку число ребер в дереве или остове графа n-1, где n – число вершин графа входящих в предполагаемое дерево, либо число всех вершин графа при проверке остова, то все деревья и остовы данного графа являются подмножеством всех подграфов данного графа из n-1 ребра.

Условием того, что выбранная связная группа ребер образует остов или дерево, будет наличие в ней всех вершин графа. Проверка осуществляется с помощью транспонированной матрицы инцидентности по выборке из всех ребер графа.

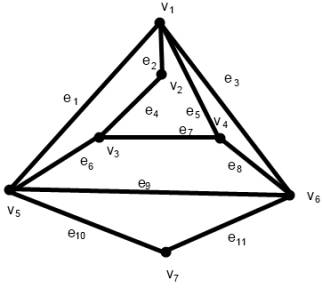
Рис 1. Пример графа

Граф в виде МБФ инциденции:

v₁v₅Úv₁v₂Úv₁v₆Úv₂v₃Úv₁v₄Úv₃v₅Úv₃v₄Úv₄v₆Úv₅v₆Úv₅v₇Úv₆v₇;

Транспонированная матрица инцидентности графа:

Номер строки соответствует номеру ребра, с нумерацией с единицы, нумерация вершин соответствует нумерации столбцов справа на лево начиная с единицы. Ниже приведен пример работы алгоритма в различных режимах на приведенном графе для подграфа e₁Úe₂Úe₃Úe₄Úe₅Úe₁₁ (нумерация ребер с единицы).

В маску записывается ребро 1 - 0010001 (вершины 1 и 5), в массив используемых ребер записываются значения 2, 3, 4, 5 и 11.

Таблица 1. Пошаговое выполнение цикла сравнения маски c элементом матрицы инцидентности операцией И

№	Маска	№ ребра	Значение ребра	Результат И	Массив номеров ребер
0	0010001				2, 3, 4, 5, 11
1	0010001	2	0000011	0000001	11, 3, 4, 5
2	0010011	11	1100000	0000000	11, 3, 4, 5
3	0010011	3	0100001	0000001	11, 5, 4
4	0110011	11	1100000	0100000	4, 5
5	1110011	4	0000110	0000010	5
6	1110111	5	0001001	0000001	-

Результат этапов 1, 3-6 отличался от нуля, поэтому на этом этапе менялось значение маски и удалялось заменой содержимое массива ребер. Так как в массиве номеров ребер не осталось значений, то программа выдаст ответ “дерево” независимо от режима. Так как число задействованных вершин равно числу вершин всего графа, то подграф является остовом графа.

Литература.

1. Костюкова Н.И. Графы и их применение. Комбинаторные алгоритмы для программистов /Костюкова Н.И. Москва, Бином, Интернет-Университет Информационных технологий. 2007г. – 311 с.

2. Кристофидес Н. Теория графов. Алгоритмический подход /Кристофидес Н. Мир, 1978г. – 432 с.

3. Ткаченко В.Г. Отказы цифровых схем и представления монотонных булевых функций / Â.Ã. Òêà÷åíêî //Íàóêîâ³ ïðàö³ ÎÍÀÇ ³ì. Î.Ñ. Ïîïîâà. – 2006. – ¹ 2. – Ñ. 45 – 69.