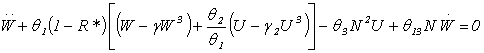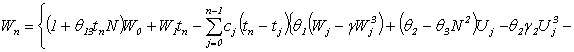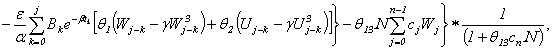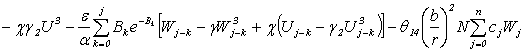Абдрахманов Р.

                                           C. Абдурахманов

Темирбеков А.Н.

Баялы А.Т

 

Международный казахско-турецкий университет имени Х.А.Ясави, г.Туркестан

Tашкентский государственный технический университет имени А.Р.Беруни, г. Ташкент

 

Исследования нелинейной задачи колебательной неустойчивости наследственно - деформируемых систем.

 

            Известно [1,2,3,4] несколько видов классического флаттера несущих поверхностей самолета, причем для обнаружения колебательной неустойчивости (автоколебания) необходимо учитывать, по крайней мере, две степени свободы колебательной системы. Типичным видом классического флаттера является изгибно-крутильный флаттер крыла самолета [1,3,4] при исследовании возможности его появления учитывает изгиб и закручивание крыла. Ниже рассматривается флаттер нелинейно наследственно-деформируемого крыла имеющего две степени свободы соответствующие вертикальному перемещению W(t) и поворота j(t).

            Тогда согласно нелинейной наследственной теории Больцмана-Вольтерра [1,6] аэродинамическая сила Р и момент М, приложенные в центральной точке профилей крыла самолета будут равны соответственно

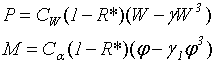                                                         ( 1)

где  и  -коэффициенты мгновенной жесткости при изгибе и кручении,  -коэффициенты физической нелинейности,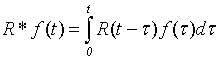

 - ядра релаксации имеющей слабо-сингулярные особенности типа Абеля, т.е.,  , Теперь согласно принципу Даламбера учитывая силу инерции и момент сил инерции из (1) получим систему уравнений движения изгибно-крутильных колебаний наследственно-деформируемого крыла

 

 

                             (2)

Здесь b - расстояние от центра жесткости до центра массы крыла; m - масса,  - радиус инерции массы относительно центральной оси.

            Наибольшие трудности представляет собой определение изменений аэродинамических сил Р, возникающих в связи с движением крыла. Если колебания происходят в потенциальном потоке газа, то на крыло всегда действуют различные возмущающие силы. Среди них самым опасным, вызывающим явлением флаттера являются аэродинамические силы, которые состоят из двух составляющих: один из которых носит название возбуждающий, действует в том же направлении, в каком идет деформация и стремится дальше увеличить последную; другой, так называемый демпфирующий, который действует в сторону противоположную возникающей деформации, и стремится вернуть крыло в положение равновесия. Подробный анализ показывает, что аэродинамические демпфирующие силы растут пропорционально скорости. А силы возбуждения растут пропорционально квадрату скорости потока [5]. В этом предположении получаем увеличение   подъемной силы и момента

                                                             (3)

где r - плотность воздуха, V - скорость потока, F - площадь крыла, a - расстояние от центра жесткости до центра давления (который расположен на одной четверти хорды крыла).

            Подставляя (3) в (2) и переходя к безмерным переменным

получим следующюю систему нелинейных интегро-дифференциальных уравнений (ИДУ)

  

 

 

 

(4)

где,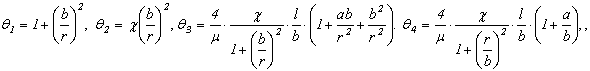 

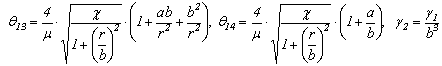
            Требуется найти из решения системы ИДУ (4), удовлетворяющих начальным условиям     (5) крити-ческую скорость флаттера Nкр.

Алгоритм численного решения нелинейных слабо-сингулярных ИДУ (4) при начальных условиях (5) строится аналогично как в [6], то есть

            (6)

  

где,

            Определение критических скоростей полета, при которых начинается флаттер или дивергенция летательного аппарата (ЛА), является одной из важнейших задач проблем аэроустойчивости ЛА. В работе это вопрос решается на основе разработанного вычислительного алгоритма [6] и специального методика поиска критической скорости, основанной на вычислительном эксперименте при заданных геометрических и механических параметрах. Согласно этой методике потери динамической устойчивости определяются из условий существования незатухающих гармонических колебаний с постоянной возрастающей амплитудой (критическое время, критическая скорость). Для всех N<Nкр т.е. сверхзвукового обтекания со скоростью потока меньшей критической скорости флаттера закон изменения W и U во времени происходит по затухающему гармоническому колебанию, а для N>Nкр с некоторого момента времени происходит начало быстрого роста амплитуды колебаний во времени т. е. происходит потери устойчивости конструкции. Для нахождения N=Nкр рассматриваются числа N1 и N2 расположенные в интервале (А,В) таким образом, что A<N1<N2<B  при  t1<t<t2. Сравнивая закон изменения W и U при N=N1 и N=N2, можно сделать следующие выводы: 1) если N<N2 при t<t1 закон изменения функции W и U близко к гармоническому, то Nкр не может в интервале (A,N1) т.е. Nкр лежит в интервале (N1,B), tкр лежит в интервале (t1<tкр<); 2) если N>N1 наблюдается быстрый рост функции W и U во времени, то  Nкр лежит в интервале  (А, N1),  tкр лежит в (0,t1).  Процесс 1) и 2) т.е. процесс исключения интервалов не происходящих нежелательных явлений повторяется для (A,N1) или (N1,B) и т.д. Поиск завершается, тогда  когда оставшийся интервал уменьшается до достаточно малых размеров.

            Анализ результатов приведенные в таблице представляет интерес по двум причинам. Во-первых, превышение критической скорости флаттера в идеально-упругом случае не означает немедленного разрушения конструкции, а разрушение наступает лишь спустя определенный период времени и носит усталостный характер. Для того, чтобы найти ожидаемый срок службы конструкции, необходимо определить амплитуду ее колебаний с учетом нелинейных и наследственно – деформируемых свойств материала конструкции. Во-вторых, критическая скорость определяемая методами идеально-упругих приближений, как в линейно, так и в нелинейно упругих постановках, оказывается лишь верхней границей критических скоростей для реальных конструкций.

            Таким образом, предложенная методика численного решения носит универсальный характер для исследования колебательной неустойчивости, т.е. автоколебания как в линейной и нелинейной идеально-упругой, так и наследственно - деформируемой крыле в потенциальном потоке газа. Как видно из таблиц учет наследственно - деформируемых свойств материала в некоторых случаях приводит почти два раза уменьшению критической скорости флаттера. В достоверности полученных результатов можно убедится сопоставлением с известными результатами других авторов. В самом деле, предлагаемая методика для линейной идеально упругого крыла без учета аэродинамических демпфирования дает Nкр=0.81, а в [1] и [2] Nкр=0.826 и Nкр=1.

            Результаты численного исследования показывает, что незначительное уменьшение параметра  сингулярности a или незначительное увеличение параметра e приводит к существенному уменьшению критической скорости флаттера. Следовательно, учет этого эффекта при проектировании конструкции ЛА имеет важное значение для обеспечения безопасности полета, так как чем меньше параметр сингулярности материала конструкции, тем  выше интенсивность диссипативных процессов в этих конструкциях.

            Учет аэродинамического демпфирования в идеально-упругом случае приводить к уменьшению, а в вязкоупругом увеличению критической скорости флаттера. Это можно объяснить тем, что поддержание аэродинамическое демпфирование незатухающих колебаний происходит только при учете реальных свойств материала конструкции.

 

 

Литература:

              1.         Бидерман В. Л. "Прикладная теория механических колебаний" М. Высшая школа ,1972. 416

              2.         Болотин В. В. "Неконсервативные задачи теории упругой устойчивости" М физматгиз 1961г.339с

              3.         Бисплингхофф Р. Л., Эшли Х., Халфмен Р. Л. "Аэроупругость". М. изд. Иностр. лит.1958 г. 799 с.

              4.         Вольмир А. С. "оболочки в потоке жидкости и газа: задачи аэроупругости " М. Наука, 1976 г. 416с.

              5.         Гроссман Е. П. "Курс вибраций частей самолета" М. оборонгиз,1940 310с.

              6.         Бадалов Ф. Б. "Методы решения интегральных и интегродифференциальных уравнений наследственной теории вязко упругости". Ташкент. "Мехнат" 1987. 269 с.

              7.         Денисов Г. Г., Новиков В. В. О влиянии внутреннего трения на устойчивость одномерных упругих систем. Сб. "Динамика систем". изд Горьковского ун-та. 1975.