12.Автоматизированные системы управления на производстве

Головицына М.В.

Профессор кафедры РЭУС Александровского филиала Московского Государственного открытого университета им. В.С.Черномырдина, к.т.н.

Формирование исходных данных при построении математических моделей технологических процессов.

Метод группировки параметров

В работах [1 – 7] автором изложена методика комплексного использования математических методов для построения «сквозных» математических моделей технологических процессов для прогнозирования качества промышленной продукции и решение задачи оптимизации для управления этим качеством.

Составной частью этой методики является необходимость формирования исходной информации для построения таких моделей. Для исследования сложного технологического процесса и управления им требуются описание, учёт, измерение и регистрация максимального количества параметров на каждой операции. Однако проведение полного перечня замеров по всему процессу в условиях производства затруднено и не всегда экономически оправдано. Поэтому уже на первых стадиях проектирования технологического процесса очень важно решение такой задачи: найти минимальное количество параметров, несущих максимальное количество информации. Другими словами, определить информативность параметров и тот процент их вклада, по которому с заданной погрешностью можно судить, что выгоднее: замерять ли этот параметр или отнести его к общей «поправке».

Для решения этой задачи целесообразно исследование различных методов и, прежде всего, методов факторного анализа для поиска обобщённых факторов и закономерностей при минимальном количестве параметров, несущих достаточную информацию о протекании процесса [3].

Поскольку сложный технологический процесс содержит большое количество параметров, имеющих разную физическую природу, то для проведения последующих факторного, корреляционно-регрессионного анализа и др., разработки математических моделей и алгоритмов управления целесообразно проводить выделение групп. Последнее основано на принципе: измеряемые параметры наиболее сильно коррелируют друг с другом в том случае, когда они наиболее сильно зависят от одного и того же фактора. Исходя из этого, все параметры технологических процессов разбиваются на группы сильно коррелирующих между собой параметров.

В групповом методе необходимо предварительно оценивать число общих факторов, кроме того, нужны и оценки общностей. Главное в групповом методе - процедура группировки параметров по признаку их наибольшей коррелированности [8].

Группировка параметров осуществляется путём максимизации функционала I, имеющего вид [8]:

,

где k - количество групп;

x_i - параметры технологического процесса;

A₁,..., A_k - группы разбиения;

F₁,...,F_k - общие факторы;

(x_i^.F_k) - парные коэффициенты корреляций.

Для поиска общих факторов используется формула

,

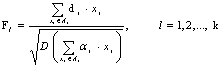где a_i - компоненты собственного вектора матрицы корреляции , соответствующие ее наибольшему собственному значению: (здесь x_i x_jÎA_l, (x_i x_j)=r_ij - парные коэффициенты корреляции);

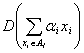- дисперсия соответствующей величины.

Блок-схема реализации на ЭВМ метода группировки параметров представлена на рис.1.

Пояснения к блок-схеме:

Блок 1. Ввод матрицы исходных данных X_ij, i=1,2,...,N; i - номер наблюдения, j - номер параметра; x₁...x_m - измеренные параметры.

Группировка параметров задается массивом А(i), i=1,2... M, где А(i) - означает номер группы, к которой принадлежит i^й параметр.

Блок 2. Нахождение матрицы корреляций y_ij; i,j=1,2...M по известным формулам (см. метод главных факторов).

Блок 3. Нормировка исходных данных осуществляется по формуле

.

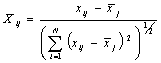Блок 4. Деление корреляционной матрицы на миноры; i^й минор состоит из элементов y_{k j} матрицы Y, таких, что А (k) = А (j) = i

Блок 5. Присвоение параметру I=1.

Блок 6. Проверка условия I £ L.

Блок 7. Определение для i ^го минора матрицы собственных значений и собственных векторов.

Блок 8. Нахождение для i-го минора номера собственного вектора с максимальным собственным значением .

Блок 9. Нахождение значения i-го фактора и печать его:

,

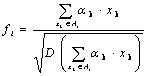где 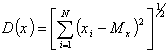- дисперсия случайной величины x;

А_i - i - группа.

Блок 10. Вычисление матрицы факторных нагрузок

где L - число групп [(x,y) - коэффициент корреляции x и у].

Блок 11. Вычисление и печать максимизирующего функционала

Блок 12. Образование нового разбиения. Параметр x_iÎ l-ой группе, если

Блок 13. Проверка условия: К1£К2? Если оно выполнено, переход на блок 4.

Блок 14. Конец.

В данном алгоритме были приняты следующие обозначения:

L - число групп разбиений для каждой итерации;

K₁ - текущий номер итерации;

К₂ - число итераций;

X(i,j) - матрица исходных данных: i - номер параметра, i=1,2,...,M;

j - номер наблюдения, j=1,...,N;

EPS1 - точность для сходимости итераций;

K_l - текущий номер итерации;

ITER - число итераций;

P1 - процент вклада дисперсии общих факторов в общность;

J(i,j) - корреляционная матрица i=1,...,М, j=1,...,M;

A(i,j) - диагональная матрица собственных значений a_ij i=1,...,М, j=1,...,М;

B(i,j) - матрица, столбцы которой - собственные векторы матрицы Y i=1,...,М, j=1,...,М;

l_i=A ( i , i )- собственные значения матрицы Y, i = 1,...,М;

- числа, переставленные так, что

- общности.

После группировки проводится поиск информативных параметров внутри групп. Для этого используются методы главных компонент и главных факторов.

Например, после обработки на ЭВМ информации по технологическим циклам изготовления видеоконтрольного устройства была получена дендрограмма.

Результаты группировки параметров (дендрограмма)

-.0575 -.0395 -.0215 -.0035 .0145 .0325 .0505 .0685 .0865 .1045 .1225 .1405 .1585

-.0575 -.0395 -.0215 -.0035 .0145 .0325 .0505 .0685 .0365 .1045 .1225 .1405 .1535

Литература

1. Головицына М.В. Методология проектирования РЭС. М.: МГОУ. 1993.

2. Головицына М.В. Проектирование автоматизированных технологических комплексов. М.: МГОУ. 2001.

3. Головицына М.В., Агаев И.А., Грозман П.Я. Применение математических методов для сжатия исходной информации при описании технологического процесса выращивания минералов. // Математические методы и АС в геологии. 1988. №12. М.: ЭИ ВИЭМС, 1988. Вып. 11 – 12.

4. Головицына М.В., Грозман П.Я., Подошва Н.В. Разработка основ моделирования и принципов построения АСУТП роста монокристаллов. Анализ функциональных связей. Т.Т.4 и 5. Научный отчёт №1384 п/с. Гос. Регистрация № 01850003079. Александров, 1985.

5. Головицына М.В. Статистический контроль качества. Методика выбора контрольных точек и контролируемых параметров. // Естественные и технические науки, 2008, №6.

6. Головицына М.В. Предварительная обработка производственной информации: сущность и необходимость. // Информационные технологии в образовании и науке, 2010. Вып.6.

7. Головицына М.В. Построение математических моделей для прогнозирования качества РЭС. // Естественные и технические науки, 2009, №3.

8. Браверман Э.М. Методы экстремальной группировки параметров и задача выделения существенных факторов. // Автоматика и телемеханика. 1970.

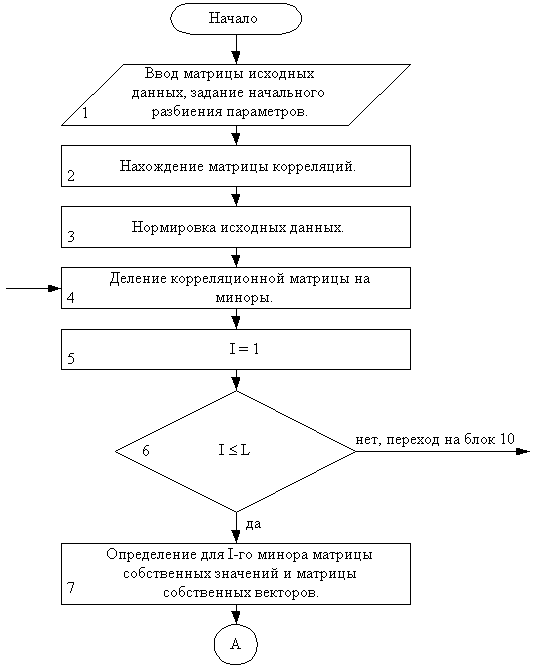
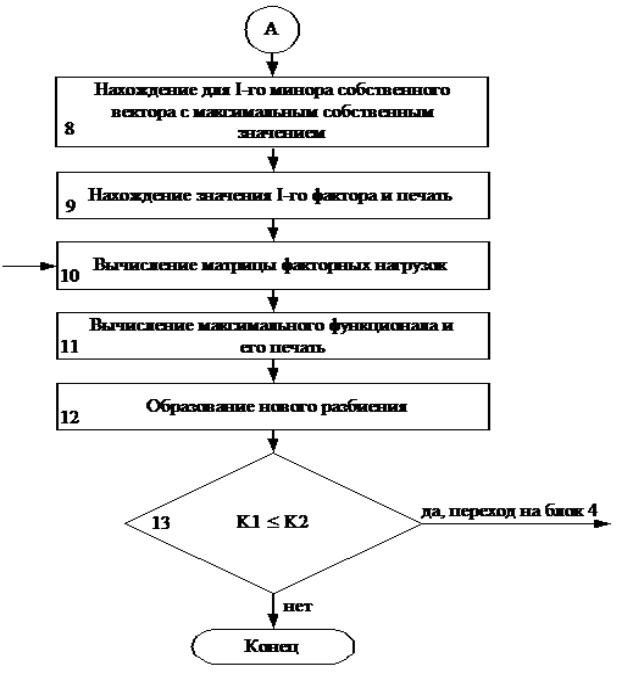
Рис.1. Блок – схема алгоритма группировки параметров