к.ф.-м.н. А.И. Долгарев
ДЕЙСТВИТЕЛЬНОЕ КОМПАКТНОЕ ЛИНЕЙНОЕ
ПРОСТРАНСТВО
Рассматриваются числовые модули и линейные пространства. Среди них имеется уникальное, это компактное пространство – мультипликативное линейное пространство комплексных чисел модуля 1 над полем действительных чисел. Указаны линейные пространства на одной группе над различными полями.
1. Числовые модули и пространства
1.1. Числовые структуры
Пусть
![]() множество чисел. На
числах определены операции сложения и умножения, возведения в степень. Сложение
и умножение коммутативны, ассоциативны и связаны свойством дистрибутивности.
Множество
множество чисел. На
числах определены операции сложения и умножения, возведения в степень. Сложение
и умножение коммутативны, ассоциативны и связаны свойством дистрибутивности.
Множество ![]() может не содержать
нуля 0, в этом случае оно обозначается
символом
может не содержать
нуля 0, в этом случае оно обозначается
символом ![]() , если оно состоит только из положительных чисел, то
используется символ
, если оно состоит только из положительных чисел, то
используется символ ![]() . Обозначения:
. Обозначения: ![]() множество натуральных
чисел,
множество натуральных
чисел, ![]() множество целых
чисел,
множество целых
чисел, ![]() множество
рациональных чисел,
множество
рациональных чисел, ![]() множество
действительных чисел,
множество
действительных чисел, ![]() множество комплексных
чисел. Вместе с внутренними операциями сложения
множество комплексных
чисел. Вместе с внутренними операциями сложения ![]() и умножения
и умножения ![]() , используются внешние операции, связанные с ними: операция
, используются внешние операции, связанные с ними: операция ![]() умножения чисел из
умножения чисел из ![]() на числа из кольца
на числа из кольца ![]() , связанная со сложением; операция
, связанная со сложением; операция ![]() возведения в степень
чисел из
возведения в степень
чисел из ![]() , связанная с умножением, показатели степени есть числа из
кольца
, связанная с умножением, показатели степени есть числа из
кольца ![]() .
.
Имеется аддитивная полугруппа ![]() и мультипликативный моноид
и мультипликативный моноид
![]() , т.к.
, т.к. ![]() ; аддитивные группы:
; аддитивные группы: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; мультипликативный моноид
; мультипликативный моноид ![]() , мультипликативные группы
, мультипликативные группы ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() , числовое кольцо
, числовое кольцо ![]() , числовые поля:
, числовые поля: ![]() ,
, ![]() ,
, ![]() .
.
Поле комплексных чисел есть расширение
поля действительных чисел мнимой единицей ![]() :
: ![]() . Имеется кольцо Гауссовых целых чисел
. Имеется кольцо Гауссовых целых чисел ![]() , это кольцо чисел вида
, это кольцо чисел вида ![]() , где
, где ![]() ; имеется поле рациональных комплексных чисел
; имеется поле рациональных комплексных чисел ![]() , оно состоит из чисел
, оно состоит из чисел ![]() , где
, где ![]() .
.
1.2. Числовые ![]() модули
модули
Напомним аксиомы ![]() модуля
модуля ![]() . На аддитивной абелевой группе
. На аддитивной абелевой группе ![]() определена операция
определена операция ![]() умножения чисел из
умножения чисел из ![]() на числа из
на числа из ![]() , связанная с операцией сложения
, связанная с операцией сложения ![]() . Для всех
. Для всех ![]() и всех
и всех ![]() выполняются следующие
условия, называемые аксиомами
выполняются следующие
условия, называемые аксиомами ![]() модуля
модуля ![]() .
.
(m.1) ![]() ; (m.2)
; (m.2) ![]() =
=![]() ;
;
(m.3) в![]() содержится 0:
содержится 0: ![]() для всех
для всех ![]() ;
;
(m.4) для всякого числа ![]() , содержащегося в
, содержащегося в ![]() , в
, в ![]() существует противоположное
число
существует противоположное
число ![]() ,
, ![]() ;
;
(m.5) ![]() =
=![]() ;
;
(m.6) ![]() ; (m.7)
; (m.7) ![]() ,
, ![]() ,
, ![]() , (если
, (если ![]() унитарно);
унитарно);
(m.8) ![]() ; (m.9)
; (m.9) ![]() ; (m.10)
; (m.10) ![]() .
.
Перечисленными
аксиомами определен аддитивный ![]() модуль
модуль ![]() =
= ![]() . В случае мультипликативного
. В случае мультипликативного ![]() модуля
модуля ![]() =
= ![]() ,
, ![]() унитарно, его аксиомы
имеют следующий вид.
унитарно, его аксиомы
имеют следующий вид.
(М.1)
![]() ;
;
(М.2)
![]() ;
;
(М.3) в ![]() содержится 1,
содержится 1, ![]() ;
;
(М.4)
для числа ![]() в
в ![]() содержится обратное число
содержится обратное число ![]() ,
, ![]() ;
;
(М.5)
![]() ;
;
(М.6)
![]() ;
;
(М.7)
![]() ;
;
(М.8)
![]() ;
;
(М.9)
![]() ;
;
(М.10)
![]() .
.
Аддитивными ![]() модулями являются
модулями являются ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Пусть ![]() ,
, ![]() . Если
. Если ![]() и
и ![]() , то
, то 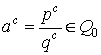 . Если
. Если ![]() и
и ![]() , то
, то 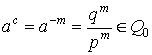 . Аксиомы (М.6) – (М.10)
возведения рациональных чисел в целую степень выполняются. Мультипликативными
. Аксиомы (М.6) – (М.10)
возведения рациональных чисел в целую степень выполняются. Мультипликативными ![]() модулями являются
модулями являются ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Если
. Если ![]() , то
, то ![]() и
и ![]() . Имеется
. Имеется ![]() модуль
модуль ![]() . Если
. Если ![]() , то число
, то число ![]() можно представить в
виде
можно представить в
виде 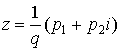 . При
. При ![]()
![]() ,
, ![]()
![]() , число
, число ![]() рациональное, число
рациональное, число ![]() рациональное
комплексное. Поэтому существует
рациональное
комплексное. Поэтому существует ![]() модуль
модуль ![]() . Кроме того, имеются
. Кроме того, имеются ![]() модули:
модули: ![]() ,
, ![]() ,
, ![]() .
.
1.3. Рациональные и действительные
линейные пространства
Существуют аддитивные линейные
пространства над полем ![]() рациональных чисел и
над полем
рациональных чисел и
над полем ![]() действительных чисел:
действительных чисел:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Положительное действительное число записывается как
экспонента
![]() .
.
Определены
операции
![]() .
.
Аксиомы
(М.1) – (М.10) выполняются. Существует мультипликативное действительное
пространство ![]() , внешняя операция на этом пространстве есть возведение
положительных действительных чисел в действительную степень:
, внешняя операция на этом пространстве есть возведение
положительных действительных чисел в действительную степень: ![]() .
.
1.4. Аддитивные комплексные линейные
пространства
Рациональное комплексное число 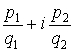 есть число вида
есть число вида 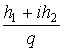 и произведение
рациональных чисел
и произведение
рациональных чисел 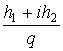
![]() является числом рациональным.
Имеется аддитивное линейное пространство
является числом рациональным.
Имеется аддитивное линейное пространство ![]() над полем
над полем ![]() :
: ![]() . Кроме того, существует
. Кроме того, существует ![]() ,
, ![]() .
.
2. Мультипликативные пространства над полем
действительных чисел
2.1. Действительное мультипликативное
линейное пространство
комплексных чисел
Всякое комплексное число ![]() , отличное от нуля, обладает тригонометрической формой записи
, отличное от нуля, обладает тригонометрической формой записи
![]() ,
,
где
![]() ,
, ![]() ,
, ![]() , действительное число
, действительное число ![]() принадлежит числовому
полуинтервалу
принадлежит числовому
полуинтервалу ![]() . Любое действительное число
. Любое действительное число ![]() представляет собой
сумму
представляет собой
сумму
![]() ; (1)
; (1)
выполняются
равенства
![]() .
.
Произведение
числа ![]() и числа
и числа ![]() есть число
есть число
![]() ,
,
т.е.
при перемножении комплексных чисел модуль произведения равен произведению модулей
сомножителей: ![]() , аргумент произведения равен сумме аргументов сомножителей:
, аргумент произведения равен сумме аргументов сомножителей: ![]() . Число
. Число ![]() , сопряженное к
, сопряженное к ![]() , равно
, равно ![]() , число, обратное числу
, число, обратное числу ![]() , есть
, есть ![]() . Имеем мультипликативную группу
. Имеем мультипликативную группу ![]() .
.
При извлечении корня ![]() ой степени из числа
ой степени из числа ![]() аргумент числа
аргумент числа ![]() вычисляется по
формуле
вычисляется по
формуле
![]() ,
, ![]() . (2)
. (2)
Введем новую операцию над комплексными числами, положив
![]() ,
, ![]() . (3)
. (3)
Здесь
![]() есть действительная
степень действительного числа, она определена однозначно. Так как
есть действительная
степень действительного числа, она определена однозначно. Так как ![]() , то существует
, то существует ![]() , что
, что ![]() . Значит,
. Значит, ![]() . Операция (3) в случае
. Операция (3) в случае ![]() не совпадает с
операцией извлечения корня
не совпадает с
операцией извлечения корня ![]() степени из комплексных чисел, которая
степени из комплексных чисел, которая ![]() значна и которая может рассматриваться как возведение числа в
степень
значна и которая может рассматриваться как возведение числа в
степень ![]() . Ниже, теорема 7, установлено, что все корни
. Ниже, теорема 7, установлено, что все корни ![]() ей степени из 1,
ей степени из 1, ![]() , содержатся в линейном пространстве над
, содержатся в линейном пространстве над ![]() корней 1. Операция
(3) альтернативна операции извлечения корня
корней 1. Операция
(3) альтернативна операции извлечения корня ![]() ой степени. Согласно (1), из действительного числа может быть
выделено слагаемое, принадлежащее интервалу
ой степени. Согласно (1), из действительного числа может быть
выделено слагаемое, принадлежащее интервалу ![]() . Операция (3) однозначна.
. Операция (3) однозначна.
1.
Теорема. Комплексные числа, отличные от нуля,
составляют муль-
типликативное линейное пространство ![]() над полем
над полем ![]() действительных чисел:
действительных чисел: ![]() .
.
# Имеем группу ![]() , т.е. аксиомы (М.1) – (М.5) для чисел из
, т.е. аксиомы (М.1) – (М.5) для чисел из ![]() выполняются. По
определению (3),
выполняются. По
определению (3), ![]() .
. ![]() , аксиома (М.7) выполняется. По (3),
, аксиома (М.7) выполняется. По (3),
![]() .
.
Произведение
чисел ![]() равно
равно
![]()
![]() =
= ![]() .
.
Действительные
степени обладают свойством ![]() . Ввиду дистрибутивности умножения действительных чисел
относительно сложения, справедливо равенство
. Ввиду дистрибутивности умножения действительных чисел
относительно сложения, справедливо равенство ![]() . В результате выделения слагаемых
. В результате выделения слагаемых ![]() , см. (1), из рассматриваемых чисел получаем слева и справа
одно число из
, см. (1), из рассматриваемых чисел получаем слева и справа
одно число из ![]() . Аксиома (М.8) выполняется в
. Аксиома (М.8) выполняется в ![]() . Далее, по определению (3), имеем с одной стороны
. Далее, по определению (3), имеем с одной стороны ![]() . И
. И ![]() =
= ![]()
![]() =
= ![]() . По свойствам действительных чисел:
. По свойствам действительных чисел: ![]() и
и ![]() . Аксиома (М.9) выполняется в
. Аксиома (М.9) выполняется в ![]() . Наконец, с одной стороны,
. Наконец, с одной стороны, ![]() =
= ![]() , с другой стороны,
, с другой стороны, ![]() и
и ![]() ,
, ![]() . Выполняется в
. Выполняется в ![]() и аксиома (М.10).#
и аксиома (М.10).#
2.
Теорема. Множеству чисел
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() , соответствует множество точек
, соответствует множество точек
![]() , составляющее
логарифмическую спираль
, составляющее
логарифмическую спираль
![]() ,
, ![]() ,
,
или в полярных координатах: ![]() . (Для сравнения [1, c. 246]).
. (Для сравнения [1, c. 246]).
# Выполнив указанные операции над
данными комплексными числами, получаем выписанные параметрические уравнения
рассматриваемого множества точек. Модуль чисел ![]() равен
равен ![]() , их аргументы есть
, их аргументы есть ![]() . Используя
. Используя ![]() и исключая параметр
и исключая параметр ![]() , приходим к уравнению линии в полярных координатах. Точки составляют
логарифмическую спираль.
, приходим к уравнению линии в полярных координатах. Точки составляют
логарифмическую спираль.
Если ![]() , то
, то ![]() и
и ![]() , тогда
, тогда ![]() и
и ![]() ,
, ![]() .#
.#
В случае ![]() имеем окружность
имеем окружность ![]() ; при
; при ![]() имеем луч
имеем луч ![]() .
.
2.2. Действительное линейное
пространство
комплексных чисел модуля 1
В мультипликативной группе ![]() выделяется подгруппа
комплексных чисел модуля 1. Теоремы п. 2.1 приобретают специфический вид. Числа
модуля 1 записываются в виде
выделяется подгруппа
комплексных чисел модуля 1. Теоремы п. 2.1 приобретают специфический вид. Числа
модуля 1 записываются в виде
![]() .
.
Если
![]() еще одно число
модуля 1, то их произведение есть
еще одно число
модуля 1, то их произведение есть ![]() и множество всех
комплексных чисел модуля 1 является мультипликативной группой
и множество всех
комплексных чисел модуля 1 является мультипликативной группой ![]() . Согласно (3),
. Согласно (3),
![]() ,
, ![]() .
.
3.
Теорема. ![]() есть мультипликативное
линейное прост-
есть мультипликативное
линейное прост-
ранство над полем ![]() действительных чисел.
действительных чисел.
#
Это частный случай теоремы 1. #
4. Теорема.
Мультипликативное линейное пространство ![]() = =
= =![]() компактно.
компактно.
# Группа ![]() изоморфна группе
поворотов плоскости вокруг фиксированного центра
изоморфна группе
поворотов плоскости вокруг фиксированного центра ![]() ; действительно, комплексное число
; действительно, комплексное число ![]() соответствует
повороту плоскости вокруг начала координат
соответствует
повороту плоскости вокруг начала координат ![]() на угол
на угол ![]() . Числу
. Числу ![]() соответствует
соответствует ![]() кратный поворот на угол
кратный поворот на угол ![]() ,
, ![]() , т.е. числам
, т.е. числам ![]() из
из ![]() соответствуют
всевозможные повороты плоскости вокруг центра
соответствуют
всевозможные повороты плоскости вокруг центра ![]() . Поворот на угол
. Поворот на угол ![]() есть
есть ![]() кратный поворот на угол
кратный поворот на угол ![]() , т.к. во множестве действительных чисел уравнение
, т.к. во множестве действительных чисел уравнение ![]() однозначно разрешимо.
По Э. Картану «На плоскости группа вращений вокруг неподвижной точки
компактна,» [2, c. 152]. Это означает, что
мультипликативное линейное пространство компактно. #
однозначно разрешимо.
По Э. Картану «На плоскости группа вращений вокруг неподвижной точки
компактна,» [2, c. 152]. Это означает, что
мультипликативное линейное пространство компактно. #
Введение внешней операции на группе не изменяет
множество, являющееся носителем этой группы: носитель ![]() группы
группы ![]() и носитель
и носитель ![]() линейного
пространства
линейного
пространства ![]() на группе
на группе ![]() один и тот же. Компактность
группы Ли
один и тот же. Компактность
группы Ли ![]() означает компактность
линейного пространства над
означает компактность
линейного пространства над ![]() , определенного на группе
, определенного на группе ![]() .
.
Установленная теорема 4 формулируется также в виде
5. Теорема.
Мультипликативное линейное пространство
над полем ![]() вращений плоскости вокруг неподвижной точки является компактным.
вращений плоскости вокруг неподвижной точки является компактным.
# Мультипликативное линейное пространство ![]() изоморфно аддитивному
линейному пространству вращений плоскости вокруг неподвижной точки, которое
компактно. #
изоморфно аддитивному
линейному пространству вращений плоскости вокруг неподвижной точки, которое
компактно. #
2.3. Пространство ![]() и пространство корней
из 1
и пространство корней
из 1
6. Теорема.
Мультипликативное линейное пространство
![]() является 1-порожденным.
является 1-порожденным.
# Группа ![]() порождается любым
своим неединичным элементом
порождается любым
своим неединичным элементом ![]() , см. доказательство теоремы 4. #
, см. доказательство теоремы 4. #
7. Теорема.
Для всякого натурального ![]() и всякого комплексного
числа
и всякого комплексного
числа ![]() все значения
все значения ![]() содержатся в
содержатся в ![]() .
.
# Пусть ![]() , т.е.
, т.е. ![]() . Аргументы чисел
. Аргументы чисел ![]() , как известно, есть (2). Т.к.
, как известно, есть (2). Т.к. ![]() , то при
, то при ![]() аргумент числа
аргумент числа ![]() равен
равен ![]() , остальные значения корня
, остальные значения корня ![]() есть числа
есть числа ![]() .
.
Пусть ![]()
![]() . По (2),
. По (2), ![]() . Значения
. Значения ![]() являются комплексными
числами
являются комплексными
числами
![]() ,
, ![]() .
.
Аргументы
этих чисел, согласно операциям на множестве ![]() , равны
, равны
![]() .
.
Все
числа ![]() содержатся в
содержатся в ![]() . #
. #
Доказанная выше теорема 6 может быть
сформулирована в виде
8. Теорема.
Мультипликативное линейное пространство
![]() содержит линейное пространство над
содержит линейное пространство над ![]() всевозможных корней из единицы
всевозможных корней из единицы ![]() .
.
# Вместе с корнями ![]() рассматриваются и их
степени
рассматриваются и их
степени ![]() ,
, ![]() ,
, ![]() , указанные показатели степеней чисел
, указанные показатели степеней чисел ![]() составляют поле
составляют поле ![]() рациональных чисел.
Величина угла поворота может быть иррациональной, но рассматриваются
рациональные кратные поворотов. Таким образом, имеется линейное пространство
рациональных чисел.
Величина угла поворота может быть иррациональной, но рассматриваются
рациональные кратные поворотов. Таким образом, имеется линейное пространство ![]() . #
. #
Пространство ![]() не является
подпространством линейного пространства
не является
подпространством линейного пространства ![]() над полем
над полем ![]() ; у этих линейных пространств общий носитель
; у этих линейных пространств общий носитель ![]() , но различны поля, над которыми определены пространства. В
пп. 1.3 и 1.4 указаны аддитивные линейные пространства на группах
, но различны поля, над которыми определены пространства. В
пп. 1.3 и 1.4 указаны аддитивные линейные пространства на группах ![]() и
и ![]() каждое над различными
полями
каждое над различными
полями ![]() и
и ![]() .
.
9. Теорема.
Линейное пространство над ![]() поворотов плоскости
поворотов плоскости ![]() компактно.
компактно.
# Компактность группы ![]() означает и
компактность линейного пространства
означает и
компактность линейного пространства ![]() над полем
над полем ![]() , определенного на группе
, определенного на группе ![]() . #
. #
2.4. Неизоморфизм действительных
1-мерных пространств
В п. 2.2. получено 1-мерное компактное линейное
пространство над полем действительных чисел. Существует действительное линейное
пространство параллельных переносов вдоль фиксированной прямой, оно 1-мерно.
Справедлива
10. Теорема.
Существуют неизоморфные 1-мерные линейные
пространства над полем ![]() действительных чисел.
действительных чисел.
# Пространство ![]() компактно, теорема 9;
пространство параллельных переносов
компактно, теорема 9;
пространство параллельных переносов ![]() вдоль действительной
оси
вдоль действительной
оси ![]() некомпактно.
Указанные пространства неизоморфны. #
некомпактно.
Указанные пространства неизоморфны. #
Этот факт для групп Ли отмечает Э. Картан, [2, c. 152]: «На плоскости группа вращений вокруг
неподвижной точки компактна, а группа параллельных сдвигов вдоль фиксированной
прямой некомпактна».
Список литературы
1.
Долгарев А.И.
Классические методы в дифференциальной геометрии одулярных пространств.
Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.
2.
Картан
Э. Геометрия групп Ли и симметрические пространства. – М.: ИЛ – 1949. – 386 с.