УДК 687.053

Владимир Алексеевич Сучилин - д.т.н., профессор, SuchilinV@mail.ru,

ФГОУВПО «Российский государственный университет туризма и сервиса»,

г. Москва

Владимир Алексеевич Сучилин - д.т.н., профессор, SuchilinV@mail.ru,

ФГОУВПО «Российский государственный университет туризма и сервиса»,

г. Москва

Роль образования в развитии высоких технологий и бизнеса

В статье рассматривается роль образования в развитии сервисных технологий и малого бизнеса, которые широко обсуждаются в настоящее время во многих странах. Приведены практические результаты исследований и разработок студентов и аспирантов, которые могут стать основой бизнес-процессов.

Ключевые слова: образование, высокие технологии, бизнес-процессы, сервис, моделирование изделий, инновации.

При проведении занятий со студентами невольно уделяешь внимание тому, как воспринимается читаемый материал, что больше интересует студентов. И становится понятно, что часть материала, как правило, материала, не включающего сложных теоретических выкладок, не имеющего логического прикладного применения в настоящее время, т.е. актуальность и востребованность которого не очевидна, мало интересует современных студентов. Вызвано это очевидно тем, что многие из них совмещают учебу с работой, знают реальные производственные проблемы. Стараются понять возможные пути повышения эффективности на своих рабочих местах.

Значительная часть студентов, обучающихся по специальностям технического сервиса, и работают, как правило, по соответствующим направлениям. Это механики по обслуживанию и ремонту авто и бытовой техники, автодилеры, менеджеры по продажам различных изделий и товаров широкого потребления. Как было отмечено, в связи с этим, их интересуют вопросы наукоемких и высоких технологий, которые они могут использовать на своих предприятиях. Эти занятия они не пропускают и задают много вопросов.

Приведу несколько тем, которые вызвали живой интерес у студентов, с которыми приходилось вести занятия. Так студентов - швейников заинтересовали вопросы гармонии «золотого сечения», применительно к швейным изделиям. История возникновения этой задачи восходит к "Началам Евклида", называемая задачей "о делении отрезка в крайнем и среднем отношении".

В связи с этим, изучался, например вопрос моделирования юбки в системе Mathcad, который выполняли следующим образом[1]. На монитор компьютера выводили предварительно составленные аналитические зависимости, например, гофрированного параболоида вращения:

x = x(r, φ) = r [1 + (a r cos n φ)/R] cos φ,

y = y(r, φ) = r [1 + (a r cos n φ)/R] sin φ,

z = z (r) = h (1- r² / R² ),

где а – амплитуда гофров в основании поверхности; n - число вершин синусоиды на круговом плане основания поверхности; R – радиус базовой окружности параболоида в основании, относительно которой построена круговая синусоида; r – радиус верхней окружности, определяющий обхват талии, варьирующийся в интервале 0 ≤ r ≤ R ; h – высота гофрированного параболоида вращения; угол φ берется в пределах 0 ÷ 2π. В этих параметрах учитывались и значения соотношений «золотого сечения». Получали изделие, с учетом варьирования роста и размера клиента. Процесс моделирования прост и занимает мало времени.

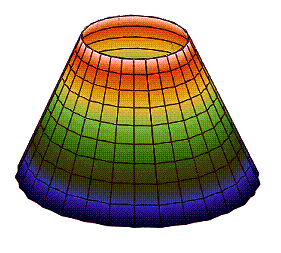
Рис. 1. Модель юбки с параметрами «золотого сечения»

В последнее время проявили интерес к этой задаче и студенты автосервиса. Действительно, современные машины очень разнятся своими формами. Как правило, дорогие машины и более гармонично смотрятся, так как при разработке их конструкторы также часто используют элементы положений «золотого сечения».

Изделия вида туристической палатки, ажурной беседки, павильона, автомобильного тента или пляжных и торговых зонтов, также легко могут моделироваться по аналитическим зависимостям. Так, например, процесс моделирования палатки осуществляется следующим образом[2]. В системе Mathcad на монитор компьютера выводятся аналитические зависимости поверхности второго порядка, например, циклоидального типа:

х = (t,γ) = а (t + Sin t ) Соs γ ,

у = (t,γ) = а (t + Sin t ) Sin γ,

z = (t) = с (1 + Соs t ),

где 0 ≤ γ ≤2π; 0 ≤ t ≤ π.

Реализация этих зависимостей в системе Mathcad при определенных значениях а и с, соответственно отвечающих за габариты изделия, на экране монитора выводится каркас палатки, имеющий то число меридиан и параллелей, которое задается предварительно. Система Mathcad позволяет поворачивать каркас палатки, изменять цвет материала, обтягивающий ее.

Важно, что аналитические зависимости, задающие форму палатки, позволяют легко определять расчетным путем ее объем и площадь расходуемого материала. А также «дорисовывать», т.е. дополнять необходимые конструктивные элементы на изделии, например, размещать, входную дверь, окна или солнечные батареи, что важно для палаток, используемых туристами, охотниками, рыбаками, геологами.

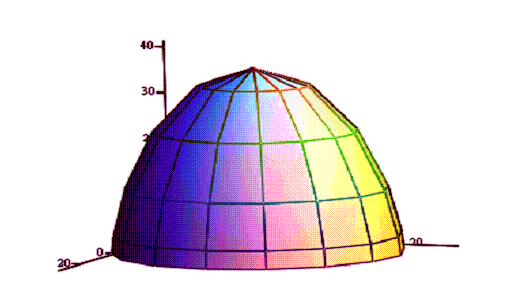
Рис.2. Форма палатки в 3-х мерных координатах

Студентам указанных специальностей уже сейчас подготовлено несколько десятков математических моделей для проектирования различных изделий, что значительно расширяет их кругозор в области наукоемких технологий и создает базу для выбора направления и создания собственного малого бизнеса .

Литература:

1.Сучилин В.А., Архипова Т.Н. К вопросу гармонии форм и золотого сечения Теоретические и прикладные проблемы сервиса, № 3(28),2008.

2. Сучилин В.А., Архипова Т.Н. Метод моделирования швейных изделий по аналитическим зависимостям, «Швейная промышленность» №5,2009