Рудницкий В.Ф, Пяткова Т.В

Северо – Казахстанский Государственный университет, Казахстан

Многомерное шкалирование

Многомерное шкалирование начало свое интенсивное развитие в 60-х годах в работах американских ученых Торгерсона , Шепарда , Краскэла . Круг советских специалистов, занимающихся этой проблемой, достаточно узок, и основные их усилия направлены на разработку формализованных методов и вычислительных процедур, реализующих известные модели на ЭВМ. К настоящему времени методы многомерного шкалирования, не получили широкого применения в педагогических исследованиях в нашей стране по ряду причин.

Задача многомерного шкалирования в самом общем виде состоит в том, чтобы выявить структуру исследуемого множества стимулов. Под выявлением структуры понимается выделение набора основных факторов, по которым различаются стимулы, и описание каждого из стимулов в терминах этих факторов. Процедура построения структуры опирается на анализ объективной или субъективной информации о близостях между стимулами либо информации о предпочтениях на множестве стимулов. В случае анализа субъективных данных решаются одновременно две задачи. С одной стороны, выявляется объективная структура субъективных данных, с другой — определяются факторы, влияющие на процесс принятия решения.
Методы многомерного шкалирования могут использовать разные типы данных: данные о предпочтениях субъекта на множестве стимулов, данные о доминировании, о близостях между стимулами, данные о профилях и т. п. Как правило, с каждым типом данных принято соотносить определенную группу методов их обработки.

В основе многомерного шкалирования лежит идея геометрического представления стимульного множества. Предположим, что нам задано координатное пространство, каждая ось которого соответствует одному из искомых факторов. Каждый стимул представляется точкой в этом пространстве, величины проекций этих точек на оси соответствуют значениям или степеням факторов, характеризующих данный стимул. Чем больше величина проекций, тем большим значением фактора обладает стимул. Мера сходства между двумя стимулами обратна расстоянию между соответствующими им точками. Чем ближе стимулы друг к другу, тем выше мера сходства между ними (и ниже мера различия), далеким точкам соответствует низкая мера сходства. Чтобы точным образом измерить близости, необходимо ввести метрику в искомом координатном пространстве; выбор этой метрики оказывает большое влияние на результат решения.

Обычно используется метрика Минковского:

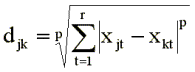
где r — размерность пространства, d_jk — расстояние между точками, соответствующими j-му и k-му стимулам, X_jt, X_kt — величины проекций j-й и k-й точек на t-ю ось.

Использование равномерных метрик предполагает, что при оценке сходств (различий) субъект в одинаковой мере учитывает все факторы. Когда же имеется основание утверждать, что факторы неравноценны для индивида и он учитывает их в разной степени, прибегают к взвешенной метрике, где каждому фактору приписывается определенный вес. Разные индивиды могут принимать во внимание разные факторы. Тогда каждый индивид характеризуется своим собственным набором весов W_tⁱ. Взвешенная метрика Минковского имеет вид:

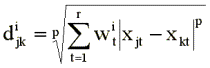
Такая модель называется «индивидуальным шкалированием» или «моделью взвешенных факторов». Геометрически она интерпретируется следующим образом. Пусть в координатном пространстве имеется конфигурация точек, отражающая восприятие некоторого «среднего индивида» в группе. Для того чтобы получить пространство восприятия i-го субъекта, необходимо растянуть «среднюю конфигурацию» в направлении тех осей, для которых W_tⁱ >W_t^ср, и сжать в направлении осей, для которых W_tⁱ <W_t^ср. Например, если в пространстве двух факторов для «среднего индивида» все стимулы лежат на окружности, то для индивида, характеризующегося весами W₁ⁱ=2, W₂ⁱ=1, эти стимулы будут располагаться на эллипсе, вытянутом вдоль горизонтальной оси, а для индивида, характеризующегося весами W₂ⁱ=2, W₁ⁱ=1, на эллипсе, вытянутом вдоль вертикальной оси.

Схема многомерного шкалирования включает ряд последовательных этапов. На первом этапе необходимо получить экспериментальным способом субъективные оценки различий. Процедура опроса и вид оценок должны выбираться исследователем в зависимости от конкретной ситуации. В результате такого опроса должна быть сконструирована субъективная матрица попарных различий между стимулами, которая будет служить входной информацией для следующего этапа.

На втором этапе решается задача построения координатного пространства и размещения в нем точек-стимулов таким образом, чтобы расстояния между ними, определяемые по введенной метрике, наилучшим образом соответствовали исходным различиям между стимулами. Для решения этой формальной задачи не требуется никаких сведений о самих стимулах, достаточно располагать только матрицей попарных различий между ними. Для построения искомого координатного пространства используется достаточно разработанный аппарат линейной или нелинейной оптимизации. Вводится критерий качества отображения, называемый «стрессом» и измеряющий степень расхождення между исходными различиями D_jk и результирующими расстояниями d_jk. Ищется такая конфигурация точек, которая давала бы минимальное значение этому «стрессу». Значения координат этих точек и являются решением задачи.

Средство повышения точности формального решения состоит в увеличении числа измерений, т. е. размерности пространства r. Чем выше размерность пространства, тем больше возможностей получить более точное решение.

Геометрическое представление стимулов в пространстве невысокого числа измерений является результатом, имеющим самостоятельное значение. Оно даст возможность наглядного представления данных, удобного для визуального анализа, и направления его использования далеко выходят за рамки психометрических исследований.

На третьем этапе решается содержательная задача интерпретации формального результата, полученного на предыдущей стадии. Координатные оси построенного стимульного пространства должны получить смысловое содержание, они должны быть проинтерпретированы как факторы, определяющие расхождения между стимулами.

Методы многомерного шкалирования предназначены для анализа структуры субъективных данных. Они позволяют выявить факторы, лежащие в основе сходств и различий между стимулами, и построить модель принятия решения о сходствах. Методы многомерного шкалирования работают только в том случае, когда сходства или различия между всеми стимулами исследуемого множества порождаются одной закономерностью.

Литература

1.Frumkina R. M., Andrukovich P. F., Terekhina A. Ju. Computational methods in the Analysis of Verbal Behaviour.—In: Computationalandmathematicallinguistics, Firence, 1976.

2.. Терехина А. Ю. Методы многомерного шкалирования и визуализации данных. Автоматика и телемеханика, № 7, 1973, с. 86-94.