Філологічні науки
Семенко
І.В., Виклюк
Н.В.
Буковинський державний
медичний університет, Чернівецький ліцей № 2 Чернівецької міської ради, Україна
Пізнавальний калейдоскоп – 3 "Золотий
переріз"
(сценарій позакласного заходу для учнів 10-11 класів та
студентів I-II курсу медичних закладів)
Цілі: - розвивати логічне та абстрактне мислення учнів,
студентів;
- показати можливість поєднання математики з філософією,
медициною, біологією за допомогою англійської мови;
- розширити знання з алгебри, геометрії, знання про
навколишній світ;
- викликати зацікавленість до вивчення математики,
дисциплін природничого циклу та англійської мови шляхом інтеграції.
Обладнання: Проектор, презентація, плакати.
І. Організаційна частина
Вчителі англійської мови та
математики вітаються з учнями, студентами повідомляють їм про продовження циклу
"Пізнавального калейдоскопу" та оголошують тему і мету заходу. (Надалі Т1 –
вчитель англійської мови, Т2 –
вчитель математики).
ІІ. Введення в іншомовне середовище
Т2 розповідає учням про
існування в науці поняття "золотого перерізу", запитує, чи знайомі учні з ним та які асоціації виникають у них,
пов’язані з цим поняттям. Після цього
Т2 звертається до учнів і пропонує
записати на дошці тільки ті поняття, які відносяться до математики.
пропорції Золотий
переріз геометричні
фігури
Піфагор Числа Фібоначчі
Евклід
Т1. Звертається до студентів
із пропозицією записати на дошці слова та
асоціації англійською мовою, які відносяться до інших наук .
Medicine Golden ratio Literature
Architecture Biology
Music
(Учні та студенти по черзі виконують завдання біля дошки,
записуючи слова на дошці та утворюючи геометричну фігуру).
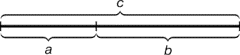
Т1 пропонує студентам вжити записані на дошці слова, утворивши речення англійською мовою. Т2 робить аналіз вище сказаного учнями та пропонує їм розглянути та записати на дошці математичне означення "золотого перерізу". Золотий переріз (золота пропорція) - пропорційне ділення відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як більша частина відноситься до меншої; або іншими словами, менший відрізок так відноситься до більшого, як більший до всього відрізку, тобто a: b = b:c або с: b = b: а.
Т1-Т2 звертають увагу учнів та
студентів на вислів німецького математика, астронома, оптика Іоганна Кеплера (1571-1630), який може стати девізом заходу.
"Геометрія володіє
двома скарбами – теоремою Піфагора і Золотим перерізом. І якщо перший з цих
двох скарбів можна порівняти з мірою золота, то другий – з коштовним
каменем".
(учні та студенти обговорюють вислів як рідною так і англійською
мовами, а також прикріплюють плакат із девізом до дошки).
Т1- Т2 звертають увагу учнів, студентів на те, що
дуже часто "Золотий переріз" асоціюється з роботою Леонардо да Вінчі
"Вітрувіанська людина". Саме
він дав цьому поняттю назву "золотий переріз".
ІІІ. Основна частина
Основна частина заходу
проводиться у вигляді міні-конференції. Після виступу, кожний доповідач на
макеті "золотого прямокутника", який зображений на дошці, за
допомогою циркуля і лінійки робить крок
"золотого поділу" і півколо спіралі Архімеда. Таким чином на дошці
утворюється спіраль Архімеда.
Student 1. Leonardo Pisano Fibonacci. Also
referred to as Leonard of Pisa, Fibonacci was an Italian number theorist. It is
believed that Leonardo Pisano Fibonacci was born in the 13th century,
in 1170 (approximately) and that he died in 1250. Fibonacci was born in Italy
but obtained his education in North Africa. Very little is known about him or
his family and there are no photographs or drawings of him. However, Fibonacci is
considered to be one of the most talented mathematicians for the Middle Ages.
Few people realize that it was Fibonacci that gave us our decimal number system
(Hindu-Arabic numbering system) which replaced the Roman Numeral system. When
he was studying mathematics, he used the Hindu-Arabic (0-9) symbols instead of
Roman symbols which didn't have 0's and lacked place value. In fact, when using
the Roman Numeral system, an abacus was usually required. There is no doubt
that Fibonacci saw the superiority of using Hindu-Arabic system over the Roman
Numerals. He shows how to use our current numbering system in his book Liber
abaci.
Учень 1.
Числовий ряд
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…, став відомим в науці
як ряд Фібоначчі. Його особливість полягає в тому, що кожний його член,
починаючи з третього, дорівнює сумі двох попередніх: 1+1=2, 1+2=3, 2+3=5,
3+5=8, 5+8=13, 8+13=21 і таке інше, а відношення чисел ряду все більш і більш
наближається до відношення золотого перерізу 2:3=0,666; 3:5= 0,6; 5:8=0,625;
8:13=0,615; 13:21=0,619; 21:34=0,617; 34:55=0,618; 55:89=0,617; 89:144=0,618;
144:233=0,618; 233:377=0,618; 377:610=0,618. Це відношення позначається символом 
. Ряд Фібоначчі залишився б тільки математичним казусом, якби не та обставина, що всі дослідники золотого перерізу
в рослинному світі, а також і у тваринному, не кажучи вже про мистецтво,
непохитно доходили до цього ряду, як до арифметичного запису закону золотого
перерізу. Твори пізанського монаха були
настільки вищі за рівень математичних знань вчених того часу, що їх вплив на
математичну науку став помітним тільки через два століття після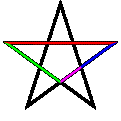 
його смерті. Відрізки
золотої пропорції виражаються нескінченними ірраціональними дробами AE = 0,618,
ВЕ = 0,382, якщо АВ прийняти за
одиницю. Для практичних цілей часто використовують наближені значення 0,62 і
0,38. Якщо відрізок АВ прийняти за 100 частин, то більша частина відрізка
дорівнює 62, а менша - 38 частинам.
Student 2. Pythagoras of Samos (b. about 570 – d. about
495 BC) was an Ionian
Greek
philosopher,
mathematician,
and founder of the religious movement called Pythagoreanism.
He was born on the island of Samos, and might have travelled widely in his youth, visiting Egypt and other places
seeking knowledge. About 530 BC, he moved to Croton,
a Greek colony
in southern
Italy, and there he set up a religious sect. His followers studied
his philosophical theories. The society took an active role in the politics of
Croton, but this eventually led to their downfall. The Pythagorean
meeting-places were burned, and Pythagoras was forced to flee the city. He is
said to have ended his days in Metapontum. Pythagoras made influential contributions to philosophy
and religious teaching in the late 6th century BC. He is often referred as a
great mathematician,
mystic
and scientist,
but he is best known for the Pythagorean Theorem which bears his name.
Учень 2. Золотий переріз можна побачити і
в пентаграмі - так називали греки зірчастий многокутник. Він служив символом піфагорійського
союзу. За їхньою теорією, в основу світового порядку покладено числа. Світ,
вважали вони, складається з протилежностей, а гармонія приводить протилежності
до єдності. Гармонія ж полягає в числових відношеннях. Піфагорійці приписували
числам різні властивості. Так, парні числа вони називали жіночими, непарні
(крім 1) - чоловічими. Число 5 - як сума першого жіночого числа (2) та першого
чоловічого (3) - вважалося символом любові. Звідси така увага до пентаграми.
Цікаво, що сторони пентаграми,
перетинаючись, утворюють правильний п'ятикутник, в якому перетин діагоналей дає
нам нову пентаграму, а в перетині її сторін знову бачимо правильний
п'ятикутник, що відкриває можливість побудови нової пентаграми. І так далі до
нескінченності. Золотий прямокутник володіє багатьма незвичними властивостями.
Відрізавши від нього квадрат, сторона якого дорівнює меншій стороні
прямокутника, ми знову отримаємо золотий прямокутник менших розмірів.
Продовжуючи відрізати квадрати, ми будемо отримувати все менші і менші золоті
прямокутники .
Student 3. Leonardo da Vinci was born on April 15, 1452, in the Tuscan
hill town of Vinci, in the lower valley of the Arno River
in the territory of the Republic of Florence. His full birth name
was "Lionardo di ser Piero da Vinci", meaning "Leonardo, (son)
of (Mes) ser Piero from Vinci". The inclusion of the title "ser"
indicated that Leonardo's father was a gentleman. Leonardo spent his first five
years in the place of Anchiano in the home of his mother, and then from 1457 lived in
the household of his father, grandparents and uncle, Francesco, in the small
town of Vinci. At the age of about fourteen Leonardo was sent to the artist Andrea del Verrocchio. During this time, Leonardo met
many of the most important artists of that time. Leonardo helped Verrocchio to paint
The Baptism of Christ,
which was completed in 1475. When Milan was invaded by the French in 1499,
Leonardo left the town and spent some time in Venice before returning to
Florence. In Florence, Leonardo lived at premises of the Servile Community, and
at that time drew the large cartoon for the Madonna and Child and St Anne
which attracted a lot of popular attention. He is also reported to have had a
job to do for King Louis XII of France. Between 1506 and 1513
Leonardo stayed in Milan. In 1513 he left Milan for Rome and was employed by
the Medici family. In 1516 the painter went to France as a court painter of
King Francis I and when the great painter died the king held his head in his hands.
Student 4. As an artist, he quickly
became master of topographic anatomy, drawing many studies of muscles, tendons and
other visible anatomical features. As a successful artist, he was given
permission to dissect human corpses at the Hospital of Santa Maria Nuevo in Florence
and later at hospitals in Milan and Rome. From 1510 to 1511 he collaborated in
his studies with the doctor Marcantonio Della Torre. Leonardo made
over 200 pages of drawings and many pages of notes towards a treatise on
anatomy. These papers were left to his heir, Francesco Melzi, for publication,
a task of overwhelming difficulty because of its scope and Leonardo's
idiosyncratic writing. It was left incomplete at the time of Melzi's death more
than fifty years later, with only a small amount of the material on anatomy
included in Leonardo's Treatise on painting, published in France in
1632. During the time that Melzi was ordering the material into chapters for
publication, they were examined by a number of anatomists and artists,
including Vasari, Cellini and Albrecht
Dürer who made a number of drawings from them. Leonardo drew
many studies of the human skeleton and its parts, as well as
muscles and sinews. He studied the mechanical functions of the skeleton and the
muscular forces that are applied to it in a manner that prefigured the modern
science of biomechanics. He drew the heart and vascular system, the sex organs
and other internal organs, making one of the first scientific drawings of a fetus in uterus. As an artist, Leonardo
closely observed and recorded the effects of age and of human emotion on the
physiology, studying in particular the effects of rage. He also drew many
figures that had significant facial deformities or signs of illness. Leonardo
also studied and drew the anatomy of many animals, dissecting cows, birds,
monkeys, bears, and frogs, and comparing in his drawings their anatomical
structure with that of humans. He also made a number of studies of horses.
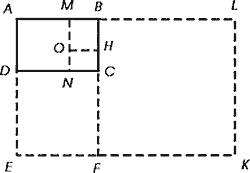
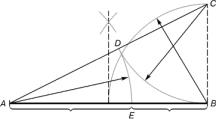Учень 3. Практичне знайомство із
золотим перерізом починається із поділу відрізка у золотій пропорції за
допомогою циркуля і лінійки.
З точки В будуємо перпендикуляр, що дорівнює
АВ. Отримана
точка з’єднується відрізком із точкою А. На отриманій прямій відкладається
відрізок ВС, що закінчується точкою D. Відрізок AD переноситься на пряму АВ.
Отримана при цьому точка Е ділить відрізок АВ у співвідношенні золотої
пропорції.
Student 5. Michelangelo di Lodovico
Buonarroti Simoni (6 March 1475 – 18 February 1564). All the people in the world
know him as Michelangelo an Italian
Renaissance sculptor, painter, architect, poet,
and engineer who exerted an unparalleled influence on the development of Western art.
Despite making few forays beyond the arts, his versatility in the disciplines
he took up was of such a high order that he is often considered a contender for
the title of the archetypal Renaissance man, along with fellow Italian Leonardo da
Vinci. Michelangelo was considered the greatest living artist in his lifetime, and
ever since then he has been held to be one of the greatest artists of all time.
A number of his works in painting, sculpture, and architecture rank among the
most famous in existence. His output in every field during his long life was
prodigious; when the sheer volume of correspondence, sketches, and
reminiscences that survive is also taken into account; he is the
best-documented artist of the 16th century. Two of his best-known works, the Pietà and David, were sculpted before he turned
thirty. Despite his low opinion of painting, Michelangelo also created two of
the most influential works in fresco in the history of Western art: the scenes from Genesis
on the ceiling and The Last Judgment on
the altar wall of the Sistine Chapel in Rome. As an architect,
Michelangelo pioneered the Mannerist style at the Laurentian Library. At 74 he succeeded Antonio da Sangallo the Younger
as the architect of St. Peter's Basilica. Michelangelo
transformed the plan, the western end being finished to Michelangelo's design,
the dome being completed after his death with some modification. In a
demonstration of Michelangelo's unique standing, he was the first Western
artist whose biography was published while he was alive. In his lifetime he was
also often called Il Divino ("the divine one").
Учень 4. Художники, вчені,
модельєри, дизайнери роблять свої розрахунки, креслення або ескізи, виходячи із
співвідношення золотого перерізу. Вони використовують пропорції тіла людини,
яке підпорядковується золотому перерізу. Леонардо Да Вінчі і Ле Корбюзье перед
тим як створювати свої шедеври брали параметри людського тіла, створеного за
законом золотої пропорції. Пропорції різних частин нашого тіла становлять
число, дуже близьке до золотого перерізу. Якщо ці пропорції збігаються із
золотим перерізом, то зовнішність або тіло людини вважається ідеальними.
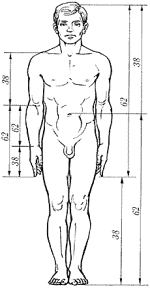Приклади золотого
перерізу в будові тіла людини:
·
відстань від кінчиків пальців до зап'ястя і від зап'ястя до ліктя - 1:1.618;
·
відстань від рівня плеча до верхівки голови й розміру голови - 1:1.618;
·
відстань від точки пупа до маківки голови і від рівня плеча до верхівки
голови - 1:1.618;
·
відстань точки пупа до колін і від колін до стопи -1:1.618;
·
відстань від кінчика підборіддя до кінчика верхньої губи і від кінчика верхньої губи до ніздрів
- 1:1.618;
·
відстань від кінчика підборіддя до верхньої лінії брів і від верхньої лінії
брів до верхівки - 1:1.618;
·
відстань від кінчика підборіддя до верхньої лінії брів і від верхньої лінії
брів до верхівки - 1:1.618.
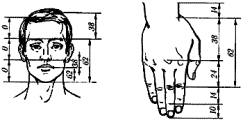На людському обличчі
існують правила золотого перерізу. Наведемо кілька таких співвідношень:
·
висота / ширина обличчя;
·
центральна точка з'єднання губ до основи носа / довжина носа;
·
відстань від кінчика підборіддя до центральної точки з'єднання губ;
·
ширина рота / ширина носа;
·
ширина носа / відстань між ніздрями;
·
відстань між зіницями / відстань між бровами.
Учень 5. Рука людини. Достатньо лише наблизити нашу
долоню до себе і уважно подивитися на вказівний палець, ми одразу бачимо в
ньому формулу золотого перетину. Кожен палець нашої руки складається з трьох
фаланг. Сума двох перших фаланг пальця у співвідношенні з усією довжиною пальця
і дає число золотого перерізу (за винятком великого пальця). Крім того,
співвідношення між середнім пальцем і мізинцем також дорівнює числу золотого
перерізу. У людини 2 руки, пальці на кожній руці складаються з 3 фаланг (за
винятком великого пальця). На кожній руці є по 5 пальців, тобто всього 10, але
за винятком двох двухфалангових великих пальців тільки 8 пальців створено за
принципом золотого перетину. Тоді як всі ці цифри 2, 3, 5 і 8 є числа
послідовності Фібоначчі.
Student 6. Archimedes of Syracuse (Greek: Ἀρχιμήδης; c. 287 BC – c. 212 BC) was a Greek
mathematician, physicist, engineer, inventor, and astronomer. He is regarded as one of
the leading scientists
in classical antiquity. Among his advances in physics
are the foundations of hydrostatics, statics
and an explanation of the principle of the lever. He is credited with
designing innovative machines, including siege engines
and the screw pump that bears his name. Modern
experiments have tested claims that Archimedes designed machines capable of
lifting attacking ships out of the water and setting ships on fire using an
array of mirrors. Archimedes is generally considered to be the greatest mathematician
of antiquity and one of the greatest of all time. He used the method of exhaustion to calculate the area under the arc of a parabola
with the summation of an infinite series, and gave
a remarkably accurate approximation of pi. He also defined
the spiral bearing his name, formulae for the volumes of surfaces of revolution and an ingenious
system for expressing very large numbers. Archimedes died during the Siege of Syracuse when he
was killed by a Roman soldier despite orders that he should not
be harmed. Cicero
describes visiting the tomb of Archimedes, which was surmounted by a sphere inscribed
within a cylinder. Archimedes had proved that the sphere
had two thirds of the volume and surface area of the cylinder (including the
bases of the latter), and regarded this as the greatest of his mathematical
achievements.
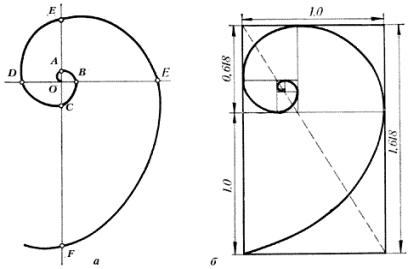
Учень 6.
"Все, що
набувало якоїсь форми, утворювалося, росло, прагнуло зайняти місце в просторі і
зберегти себе. Це прагнення знаходить здійснення в основному в двох варіантах -
зростання вгору або розстилання по поверхні землі і закручування по спіралі", казав Архімед. Форма спірально завитої раковини привернула
увагу Архімеда. Він вивчав її і вивів рівняння спіралі. Якщо її розгорнути, то виходить довжина, яка
трохи поступаться довжині змії. Невелика десяти сантиметрова раковина має
спіраль довжиною 35 см. Спіраль, побудована за цим рівнянням, називається його іменем. Спіралі дуже поширені в природі. Спіраль побачили в розташуванні
насіння соняшника, у шишках сосни, ананасах, кактусах і т.д. Спільна робота
ботаніків і математиків пролила світло на ці дивні явища природи. З'ясувалося,
що у розташуванні листя на гілці, насінні соняшнику, шишках сосни проявляє себе
ряд Фібоначчі, а отже, проявляє себе закон золотого перерізу. Павук плете
павутину спіралеподібно. Спіраллю закручується ураган. Перелякана череда
північних оленів розбігається по спіралі. Молекула ДНК закручена подвійною спіраллю.
Гете називав спіраль "кривою життя". У Всесвіті всі відомі людству
галактики і всі тіла в них існують у формі спіралі. Принципу золотого перерізу
підпорядковані і періоди обертання планет Сонячної системи.
Заключний етап заходу
Вчителі
підбивають підсумки, дякують учням і студентам та нагороджують учасників заходу
листівками, що мають форму золотого прямокутника.
Література:
1. Дюрер, Альбрехт. Дневники, письма, трактаты. Т. 1. – Л.- М.,
"Искусство", 1957. – 228с.
2. Дюрер, Альбрехт. Дневники, письма, трактаты. Т. 2. – Л.- М.,
"Искусство", 1957. – 254с.
3. Стахов, Алексей Петрович. Коды золотой пропорции. – М.: Радио и связь, 1984. – 254с.
4. Энциклопедический словарь юного математика / Сост. А.П. Савин.- М.: Педагогика, 1985. – 352с.
5. Леонардо да Винчи. Анатомия. Записи и рисунки. Пер.
с итал. М.В. Кондратьевой и З.Б. Подкопаевой.- М.: Наука. 1965. – 586с.
6. Кеплер Иоганн. О шестиугольных снежинках / Пер. с лат. Ю.А. Данилова. – М.: Наука, 1982. – 192с.
7. [електронний ресурс] http://en.wikipedia.org/wiki/Fibonacci
8. [електронний ресурс] http://en.wikipedia.org/wiki/Archimedes
9. [електронний ресурс] http://en.wikipedia.org/wiki/Michelangelo
10. [електронний ресурс] http://en.wikipedia.org/wiki/Leonardo_da_Vinci
11. [електронний ресурс] http://en.wikipedia.org/wiki/Socrates
12. [електронний ресурс]
http://www.answers.com/topic/leonardo-da-vinci
13. [електронний ресурс] http://ua-referat.com