Технические науки/10. Горное дело
Арсланов Д. М.
Южно-Уральский государственный университет, Россия
Алгоритм генерации
борта карьера
Горнодобывающие предприятия, ведущие разведку и открытую разработку месторождений твердых полезных ископаемых, составляют основу современной мировой экономики. Одной из ключевых задач управления горнодобывающим предприятием является оптимальное планирование производства открытых горных работ. Существующие оптимизационные методы для установления обоснованных границ карьеров и последовательности разработки запасов месторождения не могут быть в чистом виде применены для решения данной задачи, так как они строят только оценочные оболочки карьеров, которые имеют низкий уровень детализации. Как следствие, они дают низкую точность в расчетах, требуют большого объема ручной обработки для получения окончательного результата и не обеспечивают достаточное для оперативного решения задачи быстродействие [7].
В данной работе предложен быстродействующий алгоритм для генерации детального борта карьера, который учитывает параметры устойчивости по различным типам пород согласно геологическому строению участка недр.
Алгоритм использует воксельную модель месторождения полезных ископаемых, которая дополняет существующую классификацию моделей месторождений и способна заменить ряд разнородных моделей, используемых в горном деле для решения различных задач. Ее отличиями от регулярной блочной модели является высокая разрешающая способность дискретного мульти-скалярного поля, использование матричных преобразований, передаточных функций, интерполяции промежуточных значений, а также параллельных методов генерации и обработки графики при помощи матричных фильтров, в первую очередь ориентированных на высокопроизводительные вычисления общего назначения на графических процессорах (GPGPU) [4]. Тем самым достигается высокая точность моделирования и быстродействие.
Пусть на участке недр, изображенном на рисунке 1, залегает NR типов горных пород и подлежит добыче ND типов полезных ископаемых.
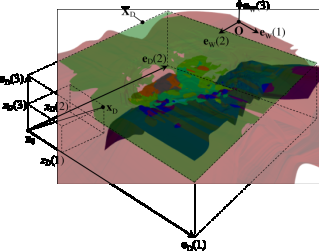
Рисунок 1 – Участок недр.
В результате обработки данных геологоразведочных и маркшейдерских работ, проведенных на рассматриваемом участке недр, в узлах g3D = (g3D(i3D)), i3D = 1, 2, 3 прямоугольной регулярной объемной решетки G3D = (g3D), показанной на рисунке 2 и представляющей собой область определения рассматриваемого участка недр, становятся известны значения трехмерных двоичных дискретных табличных функций тел горных пород R = (r(iR)), r(iR) = (r(iR, b)), iR = 1, 2, …, NR,
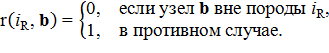
При этом узел g3D относится только к одной породе: r(iR1, b) = 1, r(iR2, b) = 0, iR1 ≠ iR2. А также становятся известны значения трехмерных вещественных дискретных табличных функций пространственного распределения содержания полезных ископаемых D = (d(iD)), d(iD) = (d(iD, b)), iD = 1, 2, …, ND, 0 ≤ d(iD, b) ≤ 1.
Связь между вектором координат g3D и вектором номеров b = (b(i3D)) узла задается следующими соотношениями:
g3D(i3D)
= (b(i3D) – 1)SB(i3D),
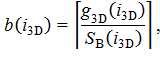
b(i3D)
= 1, 2, …, SD(i3D), 0≤ g3D(i3D) ≤ 1.
Здесь SB = (SB(i3D)) – заданные размеры ячейки объемной решетки G3D, а SD = (SD(i3D)) – ее разрешающая способность:
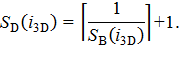
Символ ![]() обозначает округление к большему.
обозначает округление к большему.

Рисунок 2 – Прямоугольная регулярная объемная решетка участка недр.
Положение x0, размеры и ориентация объемной решетки G3D в глобальном пространстве задается при помощи матрицы перехода W = (w(iM)), iM = (iM(i2D)), iM(i2D) = 1, 2, 3, 4, i2D = 1, 2 от локального базиса ED = (eD(i3D)) решетки G3D к глобальному ортонормированному базису EW = (eW(i3D)), eW(i3D, i3D) = 1 с общим началом ортов в опорном геодезическом пункте O = (0, 0, 0):
x’0 = WO’, e’W = We’D.
Здесь штрих служит для обозначения гомогенных или однородных координат соответствующего вектора [5].
Пусть горнодобывающее предприятие планирует разработать на участке недр блоки полезных ископаемых, которые описываются трехмерной двоичной дискретной табличной функцией плана производства открытых горных работ s = (s(b)),
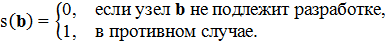
Будем описывать производство открытых горных работ трехмерной двоичной дискретной табличной функцией карьера p = (p(b)),
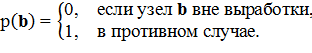
При этом разрешающая способность SD объемной решетки G3D достаточна для того, чтобы отобразить систему уступов борта карьера.
Основными параметрами уступа, показанными на рисунке 3, являются высотная отметка горизонта месторождения, высота и угол откоса, а также ширина предохранительной бермы. Значения данных параметров, обеспечивающие устойчивое положение борта карьера p, заданы для каждого типа пород iR при помощи табличных передаточных функций воксельной модели: hP = (hP(iR)), hB = (hB(iR)), aS = (aS(iR)) и wB = (wB(iR)) соответственно. С учетом функций тел горных пород R соответствующие параметры оказываются сопоставленными каждому узлу g3D объемной решетки G3D в зависимости от типа породы iR [1 – 3].

Рисунок 3 – Параметры устойчивости борта карьера.
Таким образом, проложение w(iR, b) участка борта карьера, приходящееся на высоту SB(3) ячейки объемной решетки G3D, изображенное на рисунке 3, будет зависеть от типа породы iR, в котором находится участок борта карьера, и номера b(3) горизонтального слоя объемной решетки G3D, на котором вычисляется проложение:
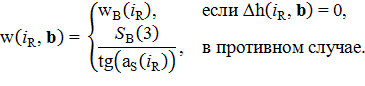
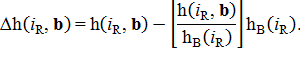
h(iR,
b) = x0(3) + SB(3)b(3) – hP(iR).
Символ ![]() обозначает округление к меньшему.
обозначает округление к меньшему.
Генерация борта карьера предлагаемым алгоритмом заключается в вычислении неизвестных значений функции карьера p по известным значениям функции плана производства открытых горных работ s.
На начальном шаге алгоритма проводится инициализация значений функции карьера p нулевыми значениями: p(b) = 0, b(i3D) = 1, 2, …, SD(i3D), i3D = 1, 2, 3. Следом проводится инициализация значений функции карьера p в узлах g3D первого горизонтального слоя объемной решетки G3D значениями функции производственного плана s в этих узлах: p(b) = s(b), b(3) = 1, b(i2D) = 1, 2, …, SD(i2D), i2D = 1, 2. На каждом следующем последовательном шаге алгоритм вычисляет новые значения функции карьера p в узлах g3D текущего горизонтального слоя объемной решетки G3D b, b(3) = 2, 3, …, SD(3) по данным нижележащего слоя
bP = b – eW(3).
Вычисления идут параллельно для каждого узла b(i2D) = 1, 2, …, SD(i2D), i2D = 1, 2. Так достигается быстродействие алгоритма.
Сечение функции карьера на текущем горизонтальном слое b объемной решетки G3D найдется как бинаризация суммарного приращения σ = (σ(b)) борта карьера по всем породам:
p(b) = Bin(σ(b)).
Бинаризация представляет собой оператор пороговой обработки вида Bin(σ) = (Bin(σ(b)),
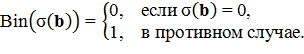
Суммарное приращение σ
вычисляется как сумма сечения функции производственного плана s на текущем слое b и приращений на величину
проложения w(iR,
bP) пересечений
I(iR, bP) карьера p с каждой породой r(iR):
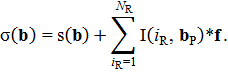
Проложение w(iR, bP) постоянно для данного пересечения I(iR, bP) в данной породе iR на данном слое bP.
Пересечение I(iR, bP) находится как произведение значений функции тела
горных пород r(iR) и функции карьера p в узлах нижележащего слоя bP:
I(iR,
bP) = r(iR,
bP)s(bP).
Приращение осуществляется за счет вычисления дискретной свертки пересечения I(iR, bP) и вещественной дискретной функции оператора генерации участка борта карьера, который представляет собой квадратный матричный фильтр f = (f(iF)), iF = (iF(i3D)), iF(i2D) = 1, 2, …, SF, iF(3) = 1 обработки горизонтального слоя объемного изображения. Матрица оператора имеет нечетную размерность SF, которая определяется по радиусу оператора RF:
SF = 2RF + 1.
Радиус оператора вычисляется исходя из величины необходимого
проложения w(iR,
bP):
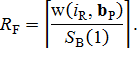
Элементы матрицы оператора принимают единичные значения в пределах круга с радиусом оператора RF, построенного вокруг центрального элемента матрицы:
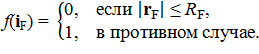
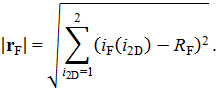
Дискретная свертка для отдельного элемента слоя находится как сумма произведений соответствующих элементов слоя и элементов фильтра в пределах полного наложения фильтра на слой, при этом центральный элемент фильтра соответствует элементу слоя, для которого ведутся вычисления:
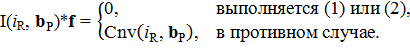
|
b(i2D) ≤ RF, |
(1) |
|
b(i2D) ≥ SD(i2D) – RF(i2D). |
(2) |
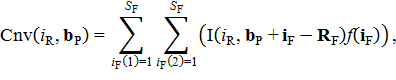
где RF = (RF, RF, 1).
Для обозначения свертки использован символ *. Действие оператора изображено на рисунке 4 [6].
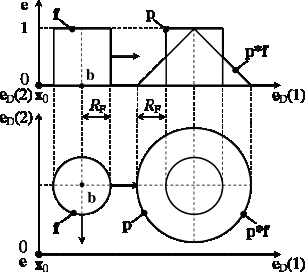
Рисунок 4 – Действие оператора генерации участка борта карьера.
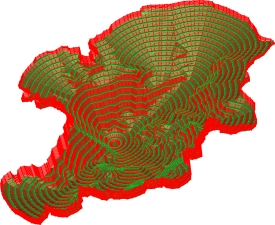
Результат построений показан на рисунке 5. Внешняя линия является пересечением с рельефом земной поверхности. Устойчивая конфигурация борта карьера точно прослеживает геологическую ситуацию на участке недр. Для построения использовалась модель с размерами 1024 x 1024 x 175 вокселей, показанная ранее на рисунке 1. Размеры вокселя составляли 2 x 2 x 2 метра. Среднее время генерации всего борта карьера составило 0,27 секунды на персональном компьютере со следующей конфигурацией: материнская плата ASRock X58 Extreme; процессор Core i7 920 (2,8 ГГц); память PC3-10666 Hynix (4 ГБ); видеокарта GTX 580 (GV-N580SO-15I); жесткий диск Corsair CSSD-F60GB2 (60 ГБ); операционная система Windows 7 Home Premium x64.
|
|
|
|
а) объемный вид |
б) вид сверху |
Рисунок 5 – Результат работы алгоритма генерации борта карьера.
Объем горной породы, вскрываемой построенным карьером, найдется как
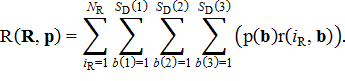
Объем добываемых полученным карьером полезных ископаемых определится как
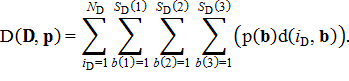
Объем извлекаемой найденным карьером пустой породы или вскрыши может быть рассчитан как
W(R,
D, p) = R(R, p) – D(D, p).
Коэффициент вскрыши построенного карьера составит
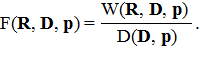
Предложенный алгоритм предназначен для применения в задачах проектирования карьера и оптимизационных методах планирования производства открытых горных работ.
Литература:
1. Единые правила безопасности при разработке месторождений полезных ископаемых открытым способом: ПБ 03-498-02: утв. Госгортехнадзором России 09.09.2002 г. – М.: Госгортехнадзор, 2002 г. – 58 с.
2. Методические указания к определению углов наклона бортов, откосов уступов и отвалов строящихся и эксплуатируемых карьеров. – Ленинград: ВНИМИ, 1972. – 165 с.
3. Ржевский В. В. Открытые горные работы: учебник для вузов. В 2 ч. Ч. 2: Технология и комплексная механизация. – 4-е изд. – М.: Недра, 1985. – 549 с.
4.
Engel,
K. Real-Time Volume Graphics / Klaus Engel, Markus Hadwiger, Joe M. Kniss,
Christof Rezk-Salama, Daniel Weiskopf. – Wellesley: A K Peters, Ltd., 2006. –
488 p.
5.
Moller,
T. Real-Time Rendering / Tomas Akenine-Moller, Eric Haines, Naty Hoffman. – 3rd
ed. – Wellesley: A K Peters, Ltd., 2008. – 1027 p.
6. NI Vision Concepts Manual: [Электронный ресурс] // National Instruments. 2005. URL: http://www.ni.com/pdf/manuals/372916e.pdf. (Дата обращения: 09.07.2012).
7. Shahriar, K. A Study On The Optimization Algorithms For Determining Open-Pit and Underground Mining Limits: [Электронный ресурс] / K. Shahriar, K. Oraee, E. Bakhtavar. // Professor Kazem Oraee publication website. Paper presented at the 7th International Scientific Conference, Sofia, Bulgaria. 2007. URL: http://www.oraee.net/shenase/Portals/0/limits.pdf. (Дата обращения: 17.12.2012).