УДК 539.3
Трубачев С.И. к.т.н.
доц., Яхно
Б.О. к.т.н. доц.
НТУУ “Киевский политехнический институт”, м. Киев, Украина
ВЛИЯНИЕ ЖЕСТКОСТИ
ОСНОВАНИЯ
НА ДЕФОРМИРОВАНИЕ
УПРУГО-ПЛАСТИЧЕСКОЙ ТРЕХСЛОЙНОЙ ПЛАСТИНЫ.
Trubachev S.І. Yakhno B.O.,
The National Technical
University of Ukraine "Kyiv Polytechnic Institute", Kyiv, Ukraine
STIFFENING EFFECT ON THE DEFORMATION OF THE THREE-LAYER
ELASTIC-PLASTIC PLATES
Аннотация. Рассмотрен изгиб
трехслойной пластины с жестким заполнителем, покоящейся на упругом основании c
учетом упруго-пластических деформаций в несущих слоях. Для описания кинематики
пакета используется гипотеза ломаной линии. Реакция основания описывается
моделью Винклера. На
контуре пластины предполагается наличие жесткой диафрагмы, препятствующей относительному
сдвигу слоев. Проведен численный расчет трехслойной пластины МКЕ пакетом ABAQUS. Была определена
зависимость пластических деформаций в слоях от коэффициента жесткости
основания. Были приведены рекомендации о выборе коэффициента жесткости на основе
прогиба.
Ключевые
слова: изгиб, трехслойная пластина, жесткий заполнитель, упруго-пластические
деформации.
Abstract. Elastic-рlastic rectangular sandwich plate lying on elastic foundation is
considered. Вreak line
hypothes is accepted for description of base layers kinematics. The foundation
reaction is described by Winkler’s model. The presence of rigid diaphragm
impeding the relative shift of layers is presumed on the contour of the plate. The
variational Lagrange’s principle is used for receiving differential system of
equilibrium equations. The numerical calculation of
the sandwich plate was done by finite element package
ABAQUS . The dependence of plastic deformation from
bending stiffness of the base was determined. Were given
advice on the choice of stiffness on the deflection. The analytical solutions of the problem have
been found and their numerical analysis has been conducted.
Keywords: bending, three-layer plate, the
rigid filler, the elastic-plastic deformation
ВВЕДЕНИЕ
В
настояще время известно много работ, посвященных исследованию пластин из
композиционных материалов, но только малая часть приходится на исследование
напряженно-деформированного состояния с учетом пластических деформации в
несущих слоях. Некоторые вопросы упругого деформирования трехслойных пластин на
упругом основании были изложены в работах Старовойтова Е.И. Горшкова О.В.,
Плескачевського Ю. М., и других авторов [1-4]. Важным достижением в области
материаловедения стало создание композитных трехслойных конструкций, которые по
механическим свойствам значительно превосходят конструкции из традиционных
материалов, причем это преимущество увеличивается при работе в повышенных
температурах и других экстремальных условиях. Поэтому разработка аналитической
и численной методики расчета и анализ напряженно-деформированного состояния
трехслойной пластины с учетом пластических деформаций в несущих слоях является
актуальной проблемой. В настоящее время промышленность постоянно выдвигает
задачу создания новых высокопрочных конструкций из композиционных материалов,
которые позволяют решать проблемы по значительному снижению веса и повышению
надежности и длительной прочности.
Использование
композитных пластин в нагруженных конструкциях является одним из способов улучшения
весовых характеристик аэрокосмической техники, в транспортном машиностроении и
строительной практике. Трехслойные пластины в условиях деформации изгиба
оказываются наиболее рациональными с точки зрения прочности и жесткости [5,6].
Таким образом, расчет трехслойных конструкций под действием статических
нагрузок с учетом пластических деформаций является актуальной задачей.
Целью работы
является построение численного алгоритма анализа
деформации
трехслойной
пластины на
упругом основании
с учетом пластических
деформаций.
1.ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ.
Рассмотрим трехслойную
пластину
с жестким
заполнителем,
находящуюся на
упругом основании.
Для описания
кинематики
пакета приняты гипотезы ломаной линии:
в несущих
слоях справедливы гипотезы Кирхгофа, в заполнителе нормаль остается прямолинейной,
не меняет
своей длины,
но поворачивается
на некоторый дополнительный
угол, составляя с координатными
осями величины ![]() ,
,![]() . Деформации считаем малыми. На пластину действуют внешние распределенные поверхностные нагрузки
. Деформации считаем малыми. На пластину действуют внешние распределенные поверхностные нагрузки ![]() ,
, ![]() ,
, ![]() а также реакция
основания (рис.1). Реакция основания
а также реакция
основания (рис.1). Реакция основания ![]() соответствует
модели Винклера
соответствует
модели Винклера
![]() ; (1)
; (1)
где ![]() - коэффициент жесткости основания,
- коэффициент жесткости основания, ![]() - прогиб пластины; знак минус указывает на то, что
реакция направлена в бок, противоположный прогибу.
- прогиб пластины; знак минус указывает на то, что
реакция направлена в бок, противоположный прогибу.
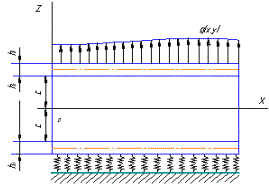

Рис. 1. Расчетная схема трехслойной пластины на
упругом основании.
Система координат
x, y, z связывается с серединной плоскостью заполнителя. Через ![]() ,
, ![]() ,
, ![]() обозначены прогиб и осевые продольные
перемещения срединной поверхности заполнителя. По контуру пластины предусматривается наличие жесткой
диафрагмы, которая препятствует
относительному сдвигу слоев. Обозначим через
обозначены прогиб и осевые продольные
перемещения срединной поверхности заполнителя. По контуру пластины предусматривается наличие жесткой
диафрагмы, которая препятствует
относительному сдвигу слоев. Обозначим через ![]() толщину
толщину ![]() - го слоя, при этом
- го слоя, при этом ![]() (k = 1, 2, 3).
(k = 1, 2, 3).
Используя введенные
геометрические гипотезы, продольные перемещения в слоях ![]() можно выразить
через пять искомых функций
можно выразить
через пять искомых функций ![]() [ 3 ].
[ 3 ].
![]() ,
,
![]()
![]() ,
, ![]() ,
, ![]()
![]() , (2)
, (2)
![]() ,
, ![]()
![]()
где ![]() - расстояние от
рассматриваемого волокна до срединной плоскости заполнителя,
- расстояние от
рассматриваемого волокна до срединной плоскости заполнителя, ![]() - величина смещения
внешнего слоя за счет деформации заполнителя, для второго несущего слоя это
смещение будет соответственно
- величина смещения
внешнего слоя за счет деформации заполнителя, для второго несущего слоя это
смещение будет соответственно ![]()
Компоненты тензора
деформаций выражаются через пять искомых функций с помощью соотношений Коши и выражений
(2):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (3)
(3)
![]()
![]()
![]()
![]()
![]()
![]()
Шаровая и девиаторная части тензора
деформаций в рассматриваемом случае будут следующими ![]()
![]()
![]()
![]()
![]()
![]()
![]() (4)
(4)
Введем внутренние усилия и моменты следующими соотношениями:
![]()
![]()
![]()
![]()
![]() (5)
(5)
![]()
![]()
![]()
где ![]() ,
,![]() ,
,![]() ,
,![]() - компоненты тензора напряжений в слоях пластины; интегралы берутся по толщине
- компоненты тензора напряжений в слоях пластины; интегралы берутся по толщине ![]() - го слоя.
- го слоя.
Уравнения равновесия находим из принципа возможных перемещений:
![]() (6)
(6)
Здесь вариация работы внешних поверхностных сил:
![]() (7)
(7)
Вариация работы внутренних сил учитывает работу
заполнителя в
тангенциальном
направлении:
![]() (8)
(8)
Вариации перемещений в слоях:![]() ,
,
![]()
![]() ,
,
![]() ,
, ![]()
![]() , (9)
, (9)
![]() ,
,
![]()
![]()
Подставив выражения
для интегралов
по толщине
слоев в формулу (8), и приравняем нулю коэффициенты при независимых
вариациях,
получим систему
дифференциальных
уравнений равновесия
прямоугольной
трехслойной
пластины на
упругом основании
в усилиях:
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() , (10)
, (10)
Для связи напряжений
и деформаций в слоях используем соотношение закона Гука в девиаторно-шаровой форме:
![]() ,
, ![]()
![]() (11)
(11)
где ![]() - модули сдвига и объемной деформации,
- модули сдвига и объемной деформации, ![]() ,
,![]() - девиаторная и шаровая части тензора напряжений,
- девиаторная и шаровая части тензора напряжений, ![]() - девиаторная и шаровая части тензора деформаций.
- девиаторная и шаровая части тензора деформаций.
Компоненты тензора напряжений в слоях с учетом
выражений (5) и (11) примут следующий вид:
![]()
![]()
![]()
![]()
![]() (12)
(12)
где ![]()
![]()
Подставляя в (8) выражение деформаций через искомые перемещения (3), и используя интегрирование по толщине каждого
из слоев,
и учитывая
выражения
(7), (6) и (1) получим из (10) систему пяти линейных дифференциальных
уравнений равновесия
относительно искомых
перемещений:
![]()
![]()
![]()
![]()
![]() (13)
(13)
де ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Принимаются
граничные условия, которые соответствуют свободному опиранию пластин на
кромках. Тогда для искомых перемещений должны выполняться следующие
условия при ![]() [1]:
[1]:
![]() (14)
(14)
Для соответствия условий (14) решения системы
дифференциальных уравнений (13) принимается в виде разложения в двойные тригонометрические ряды [2,3]
![]() ,
, ![]() ,
, ![]()
![]()
![]() , (15)
, (15)
где ![]() - неизвестные амплитуды перемещений.
- неизвестные амплитуды перемещений.
Пусть продольное нагружение
![]() . Поперечную нагрузку
. Поперечную нагрузку ![]() представим в
виде разложения в двойной тригонометрический ряд:
представим в
виде разложения в двойной тригонометрический ряд:
![]()
![]() , (16)
, (16)
После подстановки перемещений (15) и нагрузки (16) в уравнения (13) получим систему
линейных
алгебраических уравнений для определения искомых амплитуд перемещений:
![]()
![]()
![]() (17)
(17)
![]()
![]()
где коэффициенты ![]() выражаются
через величины
выражаются
через величины ![]() и зависят от
параметров m і n.
и зависят от
параметров m і n.
Решение системы
(17) можно получить численно с помощью транспонированной матрицы. После определения амплитуд ![]() искомые функции
вычисляются по формулам (15).
искомые функции
вычисляются по формулам (15).
Перемещение в
несущих слоях
и заполнители
находятся
из соотношений
(2).
2.РЕЗУЛЬТАТЫ РАСЧЕТА.
Расчет производился для трехслойной пластины с размерами 1х1х0,15 м., при этом пластина моделировалась как трехмерное твердое тело, нижняя и верхняя
часть которого
изготовлена из сплава Д16Т (толщина нижнего слоя 0,04 м., толщина верхнего 0,02 м.), а средняя - из фторопласта (рис. 2а). Задача рассчитывалась в
упруго-пластической
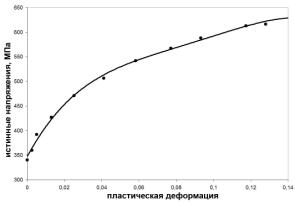
зоне. Принималось, что сплав Д16Т имеет изотропное упрочнение. Истинная диаграмма деформирования
сплава Д16Т была получена экспериментально в
работе [7]
и приведена на рис.2б.
Упругие характеристики
выбирались
для сплава
Д16Т:
модуль упругости Е =
7.66·105
МПа, коэффициент
Пуассона =
0,34, для фторопласта:
модуль упругости Е =
686,5 МПа, коэффициент Пуассона
= 0,24. Пластину нагружено давлением 40 МПа. Жесткость основы (параметр жесткости)
принимался от 0
до 10 МН / м.
|
|
|
|
а |
б |
|
Рис. 2. Свойства пластины и материала. а - геометрическая структура пластины: средний слой
- фторопласт,
внешние слои
Д16Т; б - диаграмма пластического
деформирования сплава Д16Т. |
|
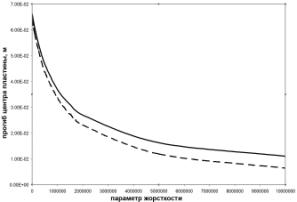
Зависимость прогиба
центра пластины от жесткости основания
приведена на рис.3,
с которого можно
видеть уменьшения
прогиба при
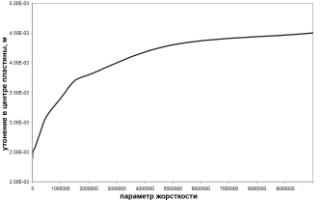
увеличении жесткости основания. При этом происходит сжатие (утонение) среднего слоя пластины (прогиб нижней поверхности меньше прогиба верхней поверхности) которое показано на рис. 3б.
|
|
|
|
а |
б |
|
Рис. 3. Прогиб и утонение в центре пластины в зависимости от
жесткости основания:
а - прогиб
центра пластины
пунктиром
показано
прогиб
нижней поверхности,
сплошной линией
- прогиб
верхней поверхности,
б - утонение пластины в ее центре. |
|
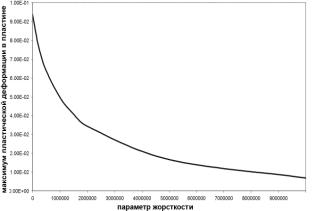
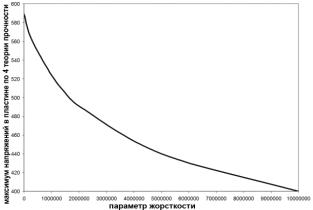
Зависимость уровня максимальной пластической деформации и
эквивалентных
напряжений по 4-й теории прочности от жесткости основания приведены на рис.4.
|
|
|
|
а |
б |
|
Рис. 4. Максимальные пластические деформации и напряжения
в пластине:
а - максимум пластической деформации
относительно
жесткости основания,
б - максимум эквивалентных напряжений
по 4-й
теории
прочности в
зависимости от жесткости основания. |
|
ВЫВОДЫ
Приведено численное решение задачи сгибания трехслойной пластины с жестким заполнителем на упругом основании
с учетом
упруго-пластических деформаций в несущих слоях. Учет жесткости упругой основы приводит к существенному уточнению напряженного состояния, возникающего
в трехслойной
пластине
при наружной
силовом воздействии.
Параметр
жорскости
рекомендуется
выбирать в зависимости
от прогиба
и упруго-пластических
деформаций несущих слоев согласно графиков приведенных на рис.3-4.
ЛИТЕРАТУРА
1.
Горшков, А. Г. Механика слоистых вязко-упругопластических элементов
конструкций / А. Г. Горшков, Э. И. Старовойтов, А. В. Яровая. – М. : Физматлит,
2005.– 576 с.
2.
Старовойтов
Э. И. Вязкоупругопластические слоистые пластины и оболочки / Э. И.
Старовойтов. – Гомель : БелГУТ, 2002. – 344 с.
3.
Старовойтов Э.И. Деформирование трехслойных элементов конструкций на упругом
основании / Э.И. Старовойтов, А.В. Яровая, Д.В. Леоненко.-М.:ФИЗМАТЛИТ, 2006. –
379 с.
4.
Плескачевский, Ю. М. Деформирование
металлополимерных систем [Текст] / Ю. М. Плескачевский, Э. И.
Старовойтов, А. В. Яровая. – Минск :
Бел. Навука, 2004. – 386 с.
5. Григолюк
Э.И., Фильштинский Л.А. Периодические кусочно-однородные упругие структуры/ Э.И. Григолюк, Л.А.Фильштинский. – М.:
Наука, 1992 .- 286 с.
6. Васильев В.В. Механика конструкций из
композитных материалов/ В.В.Васильев.-М. : Машиностроение, 1988.-288 с.
7. Яхно Б.О. Пошкоджуваність та руйнування конструкційних
матеріалів при складному малоцикловому навантаженні./ Дисертація на здобуття
наукового ступеня кандидата технічних наук. - Київ, 2005. – 150 с.
REFERENCE
1. Gorshkov,
A. G. Mehanika sloistyh vjazko-uprugoplasticheskih jelementov konstrukcij / A.
G. Gorshkov, Je. I. Starovojtov, A. V. Jarovaja. – M. : Fizmatlit, 2005.– 576 p.
2. Starovojtov,
Je. I. Vjazkouprugoplasticheskie sloistye plastiny i obolochki / Je. I.
Starovojtov. – Gomel' : BelGUT, 2002. – 344 p.
3. Starovojtov
Je.I. Deformirovanie trehslojnyh jelementov konstrukcij na uprugom osnovanii /
Je.I. Starovojtov, A.V. Jarovaja, D.V. Leonenko.-M.:FIZMATLIT, 2006. – 379 p.
4. Pleskachevskij,
Ju. M. Deformirovanie metallopolimernyh sistem [Tekst] / Ju. M. Pleskachevskij,
Je. I. Starovojtov, A. V. Jarovaja. – Minsk : Bel. Navuka, 2004. – 386 p.
5.
Grigoluk Je.I., Filshtinskiy L.
A. The periodic piece-homogeneous elastic structures / Je.I. Grigoluk, L. A.
Filshtinskiy. – M. : Science, 1992. – 286 p.
6. Vasilev V.V.
Mechanics of composite material
constructions / V.V.Vasilev.- M.: Machine-building, 1988.-288p.
7. Yakhno B.O. Damage and destruction of
constraction materials during complex low-cycle loading. / The dissertation for
scientific degree of candidate of technical Sciences. – Kiev,2005. – 150 p.